Identifying stress-induced heterogeneity in Cu20Zr20Ni20Ti20Pd20 high-entropy metallic glass from machine learning atomic dynamics
Abstract
High-entropy metallic glasses (HEMGs) are amorphous alloys with a near-equiatomic composition containing at least five elements. Such a unique non-crystalline structure with high configurational entropy of mixing provides HEMGs with promising prospects in applications, and it also attracts great scientific interest. In this paper, we focused on the atomic mechanism of stress-induced heterogeneity in the Cu20Zr20Ni20Ti20Pd20 HEMG. Applying the machine learning (ML) technique combined with the classical molecular dynamics (MD) simulation, we defined the liquid-like active atoms as the ones exhibiting high machine-learned temperature (TML). TML is a parameter to characterize the atomic motion activated by thermal and mechanical stimuli. The results reveal the stress-induced heterogeneity in atomic dynamics during creep. Local plastic flows originate from these active “hot” atoms, which have low five-fold symmetry, low coordination packing, and obvious chemical short-range ordering. Compared with conventional metallic glasses (MGs), the HEMG exhibits a smaller activation volume of creep, fewer active atoms, and sluggish dynamics. The results provide physical insights into the structural and dynamic heterogeneity in HEMGs at an atomic level.
Keywords
INTRODUCTION
High-entropy metallic glasses (HEMGs) are the conceptual combination of high entropy alloys (HEAs) and MGs. HEMGs are amorphous alloys in nature, without long-range translational symmetry. Meanwhile, HEMGs have the (near) equiatomic composition containing at least five elements, leading to a high configuration entropy of mixing. For HEAs, the most distinguishing characteristics are high entropy, sluggish diffusion, and cocktail effects[1]. However, it is unclear whether HEMGs will derive these traits from such special compositions. Many studies have reported that HEMGs possess enhanced electrocatalytic activity[2,3], excellent irradiation tolerance[4], superior cytocompatibility[5], and thermoplastic formability[6], which indicates that HEMGs have great potential for application.
Understanding the mechanical behaviors and deformation mechanisms of MGs has always been a hugely significant and challenging issue in materials science. Extensive experiment and simulation results demonstrate that they are associated with nanoscale heterogeneity[7-9]. The local plastic deformation of MGs is accommodated by flow units or referred to as “defects”. However, how to identify these “defects” from the structural and/or dynamic features is still open to discussion. On one hand, the structural descriptors attempt to distinguish the “defects” based on atomic packing, including free volume[10], quasi-punctual defects[11], local fivefold symmetry (LFFS)[12], geometrical unfavored motif[13], Qk parameter[14], and so on. On the other hand, the dynamic descriptors stress the active response to external stimulus, and hence the “defects” may be measured by soft mode[15,16] and vibrational mean squared displacement[17,18]. Compared with conventional single/double element-based MGs, HEMGs show ultrahigh strength[19,20] and enhanced intrinsic ductility[4]. A series of research on creep reported that HEMGs have a smaller serration during plastic flow[21], a smaller apparent activation volume[19,22,23], and a slower annihilation of free volume[22], than conventional MGs. Such a mechanical behavior of HEMGs is interpreted by a more homogeneous atomic arrangement[24,25] with less loose packing “defects”[24], from the structural perspective, and it is also caused by the sluggish atomic diffusion[20,26] and the inactive response of atomic motion to stress[19,26], in the view of dynamics. However, the evidence and understanding of heterogeneity at the atomic level are rare, which attracts our interest in unfolding the atomic mechanism of stress-induced heterogeneity in HEMGs.
Applying MD simulations and ML techniques, pioneering work proposed several machine-learned “defects”, such as softness[27], quench-in softness[28], structural flexibility[29], atomic-scale stiffness[30], and integrated glassy defect[31]. However, these machine-learned “defects” either only involve atomic packing without dynamics or fail in high-load/temperature conditions. This paper intended to characterize the stress-induced heterogeneity in HEMGs from learning atomic dynamics. We generated the atomic trajectories under thermal and mechanical stimuli by MD simulation, and then we used the k-nearest neighbors (kNN) ML model to quantitatively predict how an atom responds to external stimuli. According to the predicted TML, liquid-like atoms (LAs) and solid-like atoms (SAs) can be defined accordingly. The results will reveal the correlation between liquid-like “defects”, local plasticity, atomic packing symmetry, and chemical ordering.
MATERIALS AND METHODS
Classical MD simulation
Sample model preparation
As Takeuchi et al. synthesized by experiment, we prepared a Cu20Zr20Ni20Ti20Pd20 alloy model containing 50,000 atoms[32]. The simulation box had a dimension of ca. 10 × 10 × 10 nm3, and every dimension was subjected to the periodic boundary condition. The atomic interactions were computed by the
Isothermal relaxation
To analyze the atomic motion behavior at different temperatures, we simulated a series of isothermal relaxations of the HEMG sample. The HEMG sample was relaxed at specific temperatures from T = 100 K to 2000 K and zero pressure for 2.2 ns. The trajectories of all atoms in the last 200 ps were collected for subsequent ML.
Tensile test and creep
At 100 K, a uniaxial tensile simulation along the z-axis was first carried out to measure the yield strength. The tensile strain rate was set as a constant of 0.0017 ps-1, corresponding to the loading rate of
kNN ML
Dataset preparation
A multiclass classifier based on the kNN algorithm was developed for identifying temperature from atomic mobility. The initial dataset was composed of the atomic trajectories from isothermal relaxation simulations. Every atom at a given temperature corresponded to an instance in the dataset. Twenty temperatures (from T = 100 to 2000 K) were chosen as the initial class labels. Thus, the initial dataset contained one million data (= 20 T’s × 50,000 atoms). The initial 41 features for representing atomic mobility were related to the configurations at different time intervals Δt, which are listed in  (∆t)2/(Tm-1)], where
(∆t)2/(Tm-1)], where  (∆t) is the atomic displacement and m is the atomic mass.
(∆t) is the atomic displacement and m is the atomic mass.
Representative class selection and feature selection
To improve classification accuracy, it is necessary to remove indistinguishable classes and redundant features prior to learning. During the representative class selection, the initial dataset was first randomly divided into 250 subsets. For every subset, a clustering tree was constructed on the basis of the agglomerative hierarchical clustering algorithm. By the single-linkage criterion, the leaf nodes were grouped into one cluster if the distance was shorter than the cutoff of 3.6. A qualified cluster was defined as one having at least 160 leaf nodes, and it was labeled by the mode of the temperature of the leaves. As shown in Supplementary Figure 1, finally, seven representative classes were selected, i.e., T = 100, 800, 1000, 1100, 1200, 1300, and 2000 K.
Feature selection was performed by means of the ReliefF method[35]. The feature importance was evaluated by the weight:
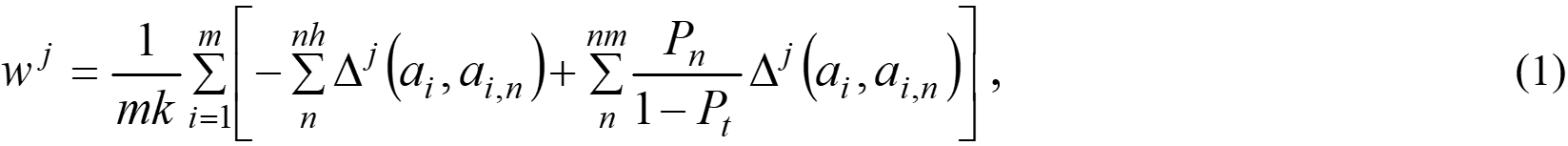
where m = 350,000 is the dataset size; k = 50 is the number of nearest neighbors, which includes nh near-hit ones and nm near-miss ones; Pt = 1/7 and Pn =1/7 are the prior probability of the class which the atom Xi and its neighbor Xi,n belong to; Δj(ai, ai,n) measures the difference in the values of feature Fj between
Hyperparameter optimization and data preprocessing
The number of nearest neighbors k was optimized by minimizing the validation root-mean-square error (RMSE). As can be seen from Supplementary Figure 3, the best k is 50. The 10-fold cross-validation was applied during the hyperparameter optimization and the following temperature predictions. Prior to training, all input data were normalized by using the min-max scaling method, which translated the data into the range of [0,1]. The ML was implemented by MATLAB R2020a.
RESULTS AND DISCUSSION
Machine-learned temperature prediction
For every testing atom, the kNN model searched the dataset and found 50 same-type nearest neighbors, which have the nearest Euclidean distance of the feature vectors. These nearest neighbors have the most similarities in these 17 features. The TML was computed by averaging the temperature class labels of its 50 nearest neighbors, and thus TML predicted which temperature class the testing atom is most likely to belong to. As shown in Figure 1A-E, there is a good linear relation between the predicted TML and the actual temperature T, although the slight deviations occur at T = 100, 800, and 2000 K, respectively. Also, this model works for all types of atoms without obvious differences. Therefore, the kNN model succeeds in recognizing the characteristics of temperature-induced atomic motion. Applying the kNN model, we can establish a correlation between temperature and individual atomic motion behavior. We must clarify the difference between the meaning of TML and thermodynamic temperature. In thermodynamics, temperature is a macroscopic quantity. In our work, however, temperatures were applied to the class labels for classification. The kNN model predicted the most probable HEMG sample that the testing atoms belong to, and this sample had a temperature of TML. Therefore, the kNN model established a correlation between an atom and a sample temperature. The TML can be understood as a temperature-like parameter that reflects the characteristic of individual atomic motion in a 200 ps time window. A high-TML “hot” atom means it is active in responding to a thermal stimulus, whereas a low-TML “cold” atom behaves in an inactive manner. Particularly with regard to the atoms with TML over glass transition temperature Tg, their atomic motion is like the atoms in supercooled liquids. Note that the active and inactive atoms are defined from atomic dynamics without relying on any structural signature, different from previous static structural parameters[10,12-14].
Machine-learned temperature in the stress-induced viscoplastic flow
In fact, the kNN model simply learns the atomic trajectories, i.e., the parameter lg[ (∆t)2/(Tm-1)], regardless of the cause of the motion. As a result, although this model is obtained from learning temperature-induced atomic motions, it can be applied to other scenarios, such as the stress-induced atomic motion from deformation. During creep, the atomic motion is activated by thermal and mechanical stimuli simultaneously[36,37]. When the kNN model predicts TML from the creep data, TML becomes a temperature-like parameter that reflects how an atom responds to the combined agitations.
(∆t)2/(Tm-1)], regardless of the cause of the motion. As a result, although this model is obtained from learning temperature-induced atomic motions, it can be applied to other scenarios, such as the stress-induced atomic motion from deformation. During creep, the atomic motion is activated by thermal and mechanical stimuli simultaneously[36,37]. When the kNN model predicts TML from the creep data, TML becomes a temperature-like parameter that reflects how an atom responds to the combined agitations.
As illustrated in Figure 2A, a tensile test was first simulated at T = 100 K to measure the σmax, which was usually defined as yielding in a simulation[38]. Subsequently, three creep stresses lower than σmax were chosen, i.e., σh = 2.2, 2.3, and 2.4 GPa. The creep curves on the holding stage are plotted in Figure 2B. The transient and steady-state creep stage can be observed on all curves, whereas the tertiary stage with the rapid increase in strain rate only occurs on the curve of σh = 2.4 GPa within the time window. During the stress holds, local irreversible atomic rearrangements are continually activated and lead to the macroscopic viscoplastic flow. According to Zhang et al., the activation volume can be fitted from the relation of the applied stress σ and steady-state strain rate  , as expressed by Ω =
, as expressed by Ω =  kBT∂ln
kBT∂ln /∂σ, where kB is Boltzmann constant[22]. The activation volume of the HEMG is 27 nm3 smaller than that of Cu50Zr50 MG (31 nm3 fitted from the curves in Ref. [34]), consistent with the experimental results[22]. Note that the smaller activation volume of the HEMG may be due to its smaller molar volume, if we assume that the HEMG sample has the same atomic packing density as the Cu50Zr50.
/∂σ, where kB is Boltzmann constant[22]. The activation volume of the HEMG is 27 nm3 smaller than that of Cu50Zr50 MG (31 nm3 fitted from the curves in Ref. [34]), consistent with the experimental results[22]. Note that the smaller activation volume of the HEMG may be due to its smaller molar volume, if we assume that the HEMG sample has the same atomic packing density as the Cu50Zr50.
Figure 2. Simulation results of tensile test and creep. (A): Stress-strain curve of tensile test. The inset illustrates the deformation of the HEMG model; (B): creep strain evolution; (C): probability density distributions of TML. ML: machine learning; HEMG: high-entropy metallic glasse.
To reveal the stress-induced heterogeneity in atomic dynamics, we applied the kNN model to predict TML for every atom. The histograms in Figure 2C statistically display the distributions of TML. If there is no applied stress on the HEMG sample, the TML will have a Gaussian distribution, which means that the atomic motion is activated by thermal agitations and corresponds to only one characteristic temperature. In Figure 2C, there is a maximum at TML = ~300 K. It is reasonable to find the peak at T = 300 K rather than 100 K because of the systematic overestimation as shown in Figure 1. This peak denotes that the majority of atoms still behave like inactive “cold” atoms and they are not fully activated by stress. Their atomic motion is still dominated by temperature, namely thermal stimulus. However, it is worth noting that there is a fat tail on the high TML side. Such a pronounced deviation from the Gaussian distribution demonstrates the stress-induced heterogeneity in atomic dynamics[34]. A small number of atoms actively respond to the mechanical stimulus and behave like active “hot” atoms, even with TML > Tg. With the increase of applied creep stress, the area of the Gauss peak falls from 82% to 67%, which means that 15% net of atoms change their motion behavior from temperature-control to stress-control. The growth of the fat tail signifies an increasing number of active atoms. We can introduce a mechanical model[34,39], which comprises a parallel arrangement of a Maxwell model and a dashpot, to understand the mechanisms of the viscoelastic and viscoplastic deformation in HEMGs. Before the active atoms coalesce, the deformation of the HEMG behaves in a viscoelastic regime. Once the active atoms outnumber the percolation threshold, overall viscoplastic flows will consequently take place[40], and the model will degenerate into a Maxwell model, which is commonly accepted for supercooled liquids[41]. Compared with Cu50Zr50[34], the less fraction of
As displayed on a 3.8-Å-thick slice in Figure 3A, the “cold” atoms form the inactive matrix and the active “hot” atoms lie in several isolated spots. Such an inhomogeneous map of TML presents the noticeable spatial heterogeneity of atomic dynamics. To unfold the correlation between atomic dynamics and local inelastic deformation, we computed the non-affine displacement D2min(∆t)[42],
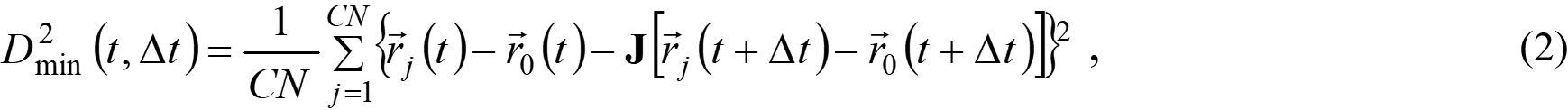
Figure 3. Correlation between TML and D2min(Δt). (A): Snapshot of a HEMG slice with the thickness of 3.8 Å, in which the atoms are colored by TML; (B-E): colored by D2min(Δt), at Δt = 5, 20, 50, 100 ps, respectively; (F): correlation coefficients between TML and
where CN is the coordination number, determined from partial radial distribution functions, as shown in Supplementary Figure 4; the subscript index j runs over the nearest neighboring atoms; j = 0 denotes the reference atom; J is the locally affine transformation matrix. Figure 3B-E visualizes D2min(∆t) on the same sample slice as shown in Figure 3A. Due to D2min(∆t) usually acting as a symbol of local inelasticity, we can observe an increasing number of inelastic deformations occur, and the severely deformed spots gradually enlarge with enhanced interactions[42]. The mounting similarity between the spatial distribution of TML and
Structural characteristics of LAs and SAs
The atoms of the same type are identical particles, and thus their difference in atomic dynamics should result from the surroundings, such as coordination, local symmetry, and chemical ordering. To characterize the signatures of atomic packing, we analyzed the Voronoi tessellation. In the following analysis, LAs and SAs are defined as 10% of the highest/lowest-TML atoms in the sample. Figure 4A includes ten of the most abundant LA- and SA-centered Voronoi polyhedra, indexed by < n3, n4, n5, n6 >, where ni denotes the number of i-edged faces in a Voronoi polyhedron. Figure 4A displays the statistical results by using columns ended with bubbles. The bubble area corresponds to the fraction of the Voronoi polyhedron among the LAs or SAs, as calculated by:
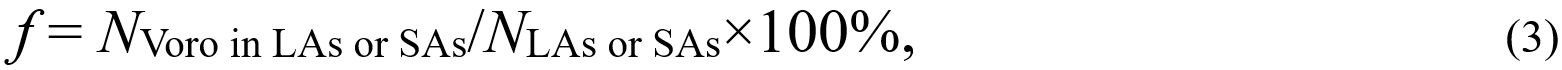
Figure 4. Atomic packing characteristics of LAs and SAs. (A): Fraction and relative deviation of the fraction from the total average for different Voronoi polyhedra; (B): the variation of Δf with LFFS. LAs: Liquid-like atoms; LFFS: local fivefold symmetry; SAs: solid-like atoms.
where NVoro in LAs or SAs is the number of the LA/SA-centered Voronoi polyhedra, and NLAs or SAs is the number of LAs or SAs. Although f reveals the abundance of certain species among the LA and SAs, f cannot reflect which polyhedron the LAs/SAs prefer because this species may be rich in both LAs and SAs. For example,

where ftotal is the total average fraction of a Voronoi polyhedron. In fact, Δf evaluates the relative deviation of f from the total average, reflecting the propensity of a Voronoi polyhedron for LAs or SAs. Still take the
For LAs, the local chemical composition and coordination may change, deviating from the total average. As shown in Figure 5A, the LAs are slightly rich in Pd, Ti, and Zr atoms, but poor in Cu and Ni atoms. The possible reason is that Cu and Ni atoms usually form icosahedra, but the LAs avoid the five-fold symmetric coordination[34,43,44]. Figure 5B compares the relative deviation of CNs of the LAs from the total average, as computed by
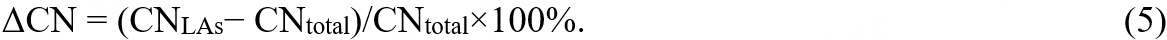
Figure 5. Chemical short-range ordering evaluation. (A): Composition of LAs, where the dashed line marks the composition of the HEMG sample; (B): relative deviation of CN, where the zero line denotes the total average; (C): matrix of parameter -αA(B). The values correspond to the total average of -αA(B), and the plus/minus signs denote how to deviate from the average. Double signs denote a significant deviation of > 0.09, and the symbol “0” means a negligible change < 0.03. CN: Coordination number; LA: liquid-like atom; SA: solid-like atom; HEMG: high-entropy metallic glasse.
Evidently, the negative ΔCN values prove the slight reduction in the CN of all LAs. With a lower CN, the LAs will acquire the loose atomic packing and share more local free volumes, which may facilitate their motion during diffusion and deformation.
Chemical short-range ordering can be measured by parameters -αA(B):[45]

where ZA(B) is the partial CN, equal to the average number of B-type atoms in the nearest coordination shell of A-type atoms; fB is the fraction of B-type atoms in HEMGs; the average CN of A-type atoms ZA = ΣXZA(X). The -αA(B) is displayed in different colors in Figure 5C, and the values are given out only for the total average. If LAs/SAs have a higher -αA(B) than the total average, the corresponding areas are marked by a plus sign, otherwise by a minus sign. The symbol “0” means the change is lower than 0.03, and the double plus/minus sign indicates the change is larger than 0.09. Firstly, the colors in Figure 5C show the chemical preference of coordination. Among all pairs, Cu-Zr, Zr-Ni, Ti-Pd, and Pd-Pd are the most favored bonds. On the contrary, Ni-Pd, Cu-Ni, Pd-Cu, and Cu-Cu pairs are relatively rare in this HEMG. It might be associated with mixing enthalpy. The favored pairs have relatively large negative mixing enthalpy, such as
CONCLUSIONS
Through learning the atomic dynamics, a kNN model successfully predicted the “temperature” of individual atoms in the Cu20Zr20Ni20Ti20Pd20 HEMG, which can serve as a parameter to identify the active/inactive atoms under thermal and mechanical stimuli. During the stress-induced plastic flow, the machine-learned temperature revealed the heterogeneity in atomic dynamics. With the increase of the applied stress, a growing number of atoms are activated and move like “hot” atoms. These active “hot” atoms show an isolated and heterogeneous spatial distribution, and they have a close connection with local plastic deformation. Structurally, the active LAs prefer the lower LFFS and less CN atomic packing. Chemically, LAs and SAs exhibit the completely opposite characteristic of chemical short-range order. Compared with the conventional MG, the HEMG has a smaller activation volume of creep, a lower fraction of active atoms that make an ineffective contribution to viscoplastic deformation, and a more pronounced chemical
DECLARATIONS
AcknowledgmentsWe thank Quanfeng He for contributing discussion on the article.
Authors’ contributionsDesigned the study and performed data analysis and interpretation: Liu X
Performed data acquisition and provided technical support: Lu W
Made substantial contributions to writing and discussion: Tu W
Made contributions to conception and supervised the research: Shen J
Availability of data and materialsNot applicable.
Financial support and sponsorshipThis work is supported by the China National Natural Science Foundation (No. 52071217).
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2022.
Supplementary MaterialsREFERENCES
1. Takeuchi A, Gao MC, Qiao J, Widom M. High-entropy metallic glasses. In: Gao MC, Yeh J-W, Liaw PK, Zhang Y, editors. High-entropy alloys: fundamentals and applications. Cham: Springer International Publishing; 2016. pp. 445-68.
2. Glasscott MW, Pendergast AD, Goines S, et al. Electrosynthesis of high-entropy metallic glass nanoparticles for designer, multi-functional electrocatalysis. Nat Commun 2019;10:2650.
3. Jia Z, Nomoto K, Wang Q, et al. A self-supported high-entropy metallic glass with a nanosponge architecture for efficient hydrogen evolution under alkaline and acidic conditions. Adv Funct Mater 2021;31:2101586.
4. Wang Y, Zhang K, Feng Y, et al. Excellent irradiation tolerance and mechanical behaviors in high-entropy metallic glasses. J Nucl Mater 2019;527:151785.
5. Cemin F, Luís Artico L, Piroli V, Andrés Yunes J, Alejandro Figueroa C, Alvarez F. Superior in vitro biocompatibility in NbTaTiVZr(O) high-entropy metallic glass coatings for biomedical applications. Appl Surf Sci 2022;596:153615.
6. Wang X, Dai W, Zhang M, Gong P, Li N. Thermoplastic micro-formability of TiZrHfNiCuBe high entropy metallic glass. J Mater Sci Technol 2018;34:2006-13.
7. Qiao J, Wang Q, Pelletier J, et al. Structural heterogeneities and mechanical behavior of amorphous alloys. Prog Mater Sci 2019;104:250-329.
8. Hu YC, Li FX, Li MZ, Bai HY, Wang WH. Five-fold symmetry as indicator of dynamic arrest in metallic glass-forming liquids. Nat Commun 2015;6:8310.
9. Gao M, Perepezko JH. Mapping the viscoelastic heterogeneity at the nanoscale in metallic glasses by static force spectroscopy. Nano Lett 2020;20:7558-65.
10. Spaepen F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metall 1977;25:407-15.
11. Perez J. Quasi-punctual defects in vitreous solids and liquid-glass transition. Solid State Ionics 1990;39:69-79.
12. Peng HL, Li MZ, Wang WH. Structural signature of plastic deformation in metallic glasses. Phys Rev Lett 2011;106:135503.
14. Rieser JM, Goodrich CP, Liu AJ, Durian DJ. Divergence of voronoi cell anisotropy vector: a threshold-free characterization of local structure in amorphous materials. Phys Rev Lett 2016;116:088001.
15. Ding J, Patinet S, Falk ML, Cheng Y, Ma E. Soft spots and their structural signature in a metallic glass. Proc Natl Acad Sci USA 2014;111:14052-6.
16. Widmer-cooper A, Perry H, Harrowell P, Reichman DR. Irreversible reorganization in a supercooled liquid originates from localized soft modes. Nat Phys 2008;4:711-5.
17. Wei D, Yang J, Jiang M, Wei B, Wang Y, Dai L. Revisiting the structure-property relationship of metallic glasses: common spatial correlation revealed as a hidden rule. Phys Rev B 2019:99.
18. Dyre JC.
19. Tong Y, Qiao J, Zhang C, Pelletier J, Yao Y. Mechanical properties of Ti16.7Zr16.7Hf16.7Cu16.7Ni16.7Be16.7 high-entropy bulk metallic glass. J Non-Cryst Solids 2016;452:57-61.
20. Kim J, Oh HS, Kim J, et al. Utilization of high entropy alloy characteristics in Er-Gd-Y-Al-Co high entropy bulk metallic glass. Acta Mater 2018;155:350-61.
21. Tong Y, Qiao J, Pelletier J, Yao Y. Rate-dependent plastic deformation of TiZrHfCuNiBe high entropy bulk metallic glass. J Alloys Compd 2019;785:542-52.
22. Zhang L, Wang Y, Pineda E, Kato H, Yang Y, Qiao J. Sluggish dynamics of homogeneous flow in high-entropy metallic glasses. Scr Mater 2022;214:114673.
23. Zhang L, Duan Y, Crespo D, et al. Identifying the high entropy characteristic in La-based metallic glasses. Appl Phys Lett 2021;119:051905.
24. Gu J, Luan H, Zhao S, et al. Unique energy-storage behavior related to structural heterogeneity in high-entropy metallic glass. Mater Sci Eng A 2020;786:139417.
25. Duan Y, Qiao J, Wada T, et al. Stress relaxation in high-entropy Pd20Pt20Cu20Ni20P20 metallic glass: experiments, modeling and theory. Mech Mater 2021;160:103959.
26. Wu J, Zhou Z, Yang H, et al. Structure related potential-upsurge during tensile creep of high entropy Al20Ce20La20Ni20Y20 metallic glass. J Alloys Compd 2020;827:154298.
27. Cubuk ED, Schoenholz SS, Rieser JM, et al. Identifying structural flow defects in disordered solids using machine-learning methods. Phys Rev Lett 2015;114:108001.
28. Wang Q, Jain A. A transferable machine-learning framework linking interstice distribution and plastic heterogeneity in metallic glasses. Nat Commun 2019;10:5537.
29. Fan Z, Ding J, Ma E. Machine learning bridges local static structure with multiple properties in metallic glasses. Mater Today 2020;40:48-62.
30. Peng Z, Yang Z, Wang Y. Machine learning atomic-scale stiffness in metallic glass. Extreme Mech Lett 2021;48:101446.
31. Yang Z, Wei D, Zaccone A, Wang Y. Machine-learning integrated glassy defect from an intricate configurational-thermodynamic-dynamic space. Phys Rev B 2021:104.
32. Takeuchi A, Wang J, Chen N, et al. Al0.5TiZrPdCuNi high-entropy (H-E) alloy developed through Ti20Zr20Pd20Cu20Ni20 H-E glassy alloy comprising inter-transition metals. Mater Trans 2013;54:776-82.
33. Zhou XW, Johnson RA, Wadley HNG. Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers. Phys Rev B 2004:69.
34. Liu X, He Q, Lu W, et al. Machine learning atomic dynamics to unfold the origin of plasticity in metallic glasses: from thermo- to acousto-plastic flow. Sci China Mater 2022;65:1952-62.
35. Robnik-Šikonja M, Kononenko I. Theoretical and empirical analysis of reliefF and RReliefF. Mach Learn 2003;53:23-69.
37. Xu Z, Qiao J, Wang J, Pineda E, Crespo D. Comprehensive insights into the thermal and mechanical effects of metallic glasses via creep. J Mater Sci Technol 2022;99:39-47.
38. Park K, Fleury E, Seok H, Kim Y. Deformation behaviors under tension and compression: atomic simulation of Cu65Zr35 metallic glass. Intermetallics 2011;19:1168-73.
39. Qiao J, Pelletier J, Yao Y. Creep in bulk metallic glasses. Transition from linear to non linear regime. Mater Sci Eng A 2019;743:185-9.
40. Wu Y, Wang B, Hu Y, et al. The critical strain - a crossover from stochastic activation to percolation of flow units during stress relaxation in metallic glass. Scr Mater 2017;134:75-9.
41. Huo L, Zeng J, Wang W, Liu C, Yang Y. The dependence of shear modulus on dynamic relaxation and evolution of local structural heterogeneity in a metallic glass. Acta Mater 2013;61:4329-38.
42. Falk ML, Langer JS. Dynamics of viscoplastic deformation in amorphous solids. Phys Rev E 1998;57:7192-205.
43. Xu TD, Wang XD, Zhang H, Cao QP, Zhang DX, Jiang JZ. Structural evolution and atomic dynamics in Ni-Nb metallic glasses: a molecular dynamics study. J Chem Phys 2017;147:144503.
44. Lu W, Tseng J, Feng A, Shen J. Structural origin of the enhancement in glass-forming ability of binary Ni-Nb metallic glasses. J Non-Cryst Solids 2021;564:120834.
45. Cargill G, Spaepen F. Description of chemical ordering in amorphous alloys. J Non-Cryst Solids 1981;43:91-7.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Liu X, Lu W, Tu W, Shen J. Identifying stress-induced heterogeneity in
AMA Style
Liu X, Lu W, Tu W, Shen J. Identifying stress-induced heterogeneity in
Chicago/Turabian Style
Liu, Xiaodi, Wenfei Lu, Wenkang Tu, Jun Shen. 2022. "Identifying stress-induced heterogeneity in
ACS Style
Liu, X.; Lu W.; Tu W.; Shen J. Identifying stress-induced heterogeneity in
About This Article
Special Issue
Copyright
Data & Comments
Data

 Cite This Article 13 clicks
Cite This Article 13 clicks

















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.