Generative models for inverse design of inorganic solid materials
Abstract
Overwhelming evidence has been accumulating that materials informatics can provide a novel solution for materials discovery. While the conventional approach to innovation relies mainly on experimentation, the generative models stemming from the field of machine learning can realize the long-held dream of inverse design, where properties are mapped to the chemical structures. In this review, we introduce the general aspects of inverse materials design and provide a brief overview of two generative models, variational autoencoder and generative adversarial network, which can be utilized to generate and optimize inorganic solid materials according to their properties. Reversible representation schemes for generative models are compared between molecular and crystalline structures, and challenges in regard to the latter are also discussed. Finally, we summarize the recent application of generative models in the exploration of chemical space with compositional and configurational degrees of freedom, and potential future directions are speculatively outlined.
Keywords
INTRODUCTION
In the course of history, material innovation has always been in the spotlight of industrial revolutions and has had an overwhelming impact on the economics. Before the 18th century, agriculture was at the core of human communities, and heavy reliance was placed on bronze and iron objects in agricultural activities [Figure 1A]. After the invention of the steam engine, mechanization began to take place, thus accelerating the industrialization of material production and creating the foundation of modern society. During this time, the technical progress of the steel manufacturing industry has made a substantive contribution to the development of railway and steamship transportation. At the end of the 19th century, electricity inaugurated its entrance on the historical scene, while the successful synthesis of organic polymers has served as another stimulus for the advancement of new technologies, such as automobiles and airplanes. Since then, the chemical industry has ushered in an era of high-speed development. Later in the 20th century came the third industrial revolution, where semiconductor materials are playing the vital role. The advent of computers and electronic technologies has revolutionized the industrial production globally and given rise to unprecedented opportunities for innovations in all aspects of our lives. To date, the uptake of computer science in material research and other realms has been highly advocated due to its unfathomable potential power. In silico materials design based on artificial intelligence and big data is becoming ever more feasible and realistic, which could constitute a new paradigm in the field of materials science[1-8].
Figure 1. Historic overview of industrial revolution and the closed-loop paradigm for materials design: (A) evolution of human society and the key materials that play an essential role; and (B) the process of forward design and the incorporation of inverse design.
The traditional materials discovery process is forward; that is, all the candidate materials that are expected to possess the desired properties will be directly synthesized and examined, until the most promising one is found. The whole process includes three steps: conjecture, synthesis, and test [Figure 1B]. Empirical physical and chemical rules are first employed to acquire the list of potential materials for study, which are then experimentally synthesized and characterized. The measured properties of these materials will be compared with each other, through which new knowledge is generated to refine the empirical rules[9]. This trial-and-error process is labor-intensive and time-consuming. In this context, inverse design is an appealing strategy to close the loop, which can help guide the exploratory research of materials discovery and mitigate the need for one-by-one material examination in the chemical space[10]. By definition, inverse design in materials science means that, given target functionality, the compositions and structures of potential materials are stringently optimized prior to experiments. To this end, we can rely on the advances in artificial intelligence, which can enable the long-held dream of fast inverse design in an arbitrarily large chemical space, identifying materials with a high probability of expected properties at the expense of acceptable computational complexity.
Machine learning, one of the most popular typologies of algorithms for artificial intelligence, has already been leveraged to achieve inverse design of both molecules and crystals[8,11-21]. This is a multidisciplinary endeavor that demands efficient structure encoding schemes and robust data management techniques. Despite being computationally efficient, this approach requires a plethora of material structures and properties for training, which generally constitutes a major obstacle for its practical application. However, the fast-paced developments in high-throughput ab initio calculations and the establishment of the corresponding database have made it possible to build machine learning models for a variety of materials. Consequently, inverse design by machine learning has risen to a prominence over conventional high-throughput ab initio calculations and stood at the frontier of in silico materials design[10].
Generative models in machine learning are especially applicable to inverse design of materials. In this review, we focus on two generative models that are most widely used in the inverse design of inorganic solid materials: variational autoencoder (VAE)[22] and generative adversarial network (GAN)[23]. The frameworks for reversible coding of molecules and solid materials are elaborated and compared, with emphasis placed on the representation schemes for the generative models. Two directions for materials inverse design are specifically discussed: compositional and structural optimization with various levels of constraints. We further highlight the major challenges and limitations faced by the inverse design of inorganic solid materials and suggest some possible solutions as well as directions worth further exploration.
INVERSE DESIGN
Inverse design in materials science requires the navigation in chemical space through calculation and simulation, for which there emerge three categories of methodologies exploited to enable material identification: (1) high-throughput screening; (2) global optimization; and (3) generative models.
High-throughput screening via ab initio calculations has been widely adopted for inverse design due to the development of ab initio calculation codes and high-performance computing hardware in the past two decades[24-26]. Starting from a portfolio of materials chosen on the basis of intuition, density functional theory or Hartree-Fock calculations are carried out for each of the materials to obtain the “predicted properties”. By sorting these materials according to the predicted properties, candidate materials can be readily found, thus obviating the need for synthesizing the whole set of chosen materials. The manual efforts spent on experiments can be greatly reduced. We would like to note that the process of high-throughput screening is akin to the forward design process, but the former relies only on computation and can be easily automated.
One of the most critical issues in high-throughput screening is to determine an appropriate chemical space. Too large chemical space will correspond to an enormous number of materials for calculation according to the permutation and combination, thus resulting in excessively high computational costs[27], while, with too small chemical space, researchers will risk disqualifying many opportunities that might actually lead to discovery of promising materials. Expertise is therefore of paramount importance in exploring the chemical space.
Global optimization is more efficient in navigating the chemical space than high-throughput screening. Unlike local optimization used in traditional ab initio calculations, global optimization algorithms focus on the entire feasible set and search for the global optimal solution by traversing all possible optimal structures in the chemical space. Representative global optimization algorithms include simulated annealing, particle swarm optimization, genetic algorithm, and simplex method. Among them, the genetic algorithm is a popular choice to determine the optimal solution in the field of materials science. We take the global optimization of clusters[28] as an example. The atomic coordinates (“genotype”) of the cluster (“population”) that need to be optimized are perturbed (“variation” or “hybridization”), and cluster configurations passing geometrical evaluation (“fine adaptability”) are preserved. By iterating the above process, new cluster populations are generated, until convergence is reached from which the final configuration is selected to be the global optimal solution.
While global optimization is quite successful for inverse design of materials, data-driven approaches, e.g., machine learning as mentioned above, could further push the frontier of this field[29]. Material databases, such as the Inorganic Crystal Structure Database (ICSD)[30], the Open Quantum Materials Database[31], and the Materials Project (MP)[32] database, have provided a wealth of material data, which can remarkably facilitate the development of data-driven materials discovery. Moreover, the combination of simulated data and machine learning may lead to the conceptualization of new chemical rules[33], thus forming a novel perspective for materials design strategies.
Generative models in machine learning can effectively learn the real distributions and are therefore suitable for inverse design. Different from the discriminant models that calculate the conditional probability of the target variable under the premise of given observation variable values, the generative models emphasize on the total probability of all variables. Therefore, generation models can be used to simulate the distribution of any variable of interest. In the tasks of image generation[34-36], text generation[37-39], video generation[40], and audio synthesis[41-43], generative models have achieved amazing performance. As the common generative models, VAE and GAN are widely used in the field of materials science and have received extensive validation.
VAE is a deep generative model based on the autoencoder [Figure 2A]. An autoencoder can be applied to problems such as dimensionality reduction and feature extraction. Its basic framework is first mapping samples to hidden variables in low-dimensional space through encoder, and then restoring the hidden variables to reconstructed samples through decoder. To improve the ability of the decoder to generate new materials rather than to derive a unique mapping, VAE maps the material to a random variable obeying the explicit definition of multivariate normal distribution through a constraint encoder. Therefore, the hidden variable Z is actually the probability distribution of the material.
Figure 2. The network structures of typical generative models: (A) variational autoencoder; (B) conditional variational autoencoder; (C) generative adversarial network; and (D) conditional generative adversarial network.
As compared with VAE, the probability density function of the hidden variables generated by GAN is implicit. GAN consists of generator and discriminator [Figure 2C], where the former is used to receive random variable Z and generate fake samples G(Z). The discriminator D receives the real sample X and the fake sample G(Z) generated by the generator at the same time and outputs the probability that G(Z) is considered to be a real sample. The results are fed back to the generator G to guide the training of G. In the process of GAN training, the generator and the discriminator update their own parameters to minimize the loss. A Nash equilibrium state is finally achieved, and the model is optimal after continuous iterative optimization.
REPRESENTATION
Despite the fruitful achievements in inverse design of molecules via generative models[20,44-46], their application in inorganic solid materials remains an outstanding challenge due to the difficulty in encoding the structures. In the following, we briefly outline some of the most typical structural representation schemes for generative models.
The wide application of generative models to the organic molecules[46,47] lies in the excellent representation schemes for molecules, which have both reversibility and symmetric invariance. Reversibility means that the digital space is mapped bijectively to real molecules, while symmetry invariance means that the representations after rotation, translation, and permutation can be identified as the same molecule before these operations. Simplified molecular input line entry system (SMILES) strings[48,49] and molecular graphs[50] are among the most renowned representation schemes [Figure 3A].
Figure 3. Representations of molecule and crystal in inverse design. (A) An example of weighted graph and SMILES string of molecule. (B) Bag-of-atoms representation for chemical composition. This figure is quoted with permission from Pathak et al.[51]. (C) Matrix representation for Mg-Mn-O ternary materials. This figure is quoted with permission from Kim et al.[52]. (D) Voxel grid representation of crystal with information from CIF file. This figure is quoted with permission from Hoffmann et al.[53]. (E) Image representation of atomic position by Gaussian kernel distribution. This figure is quoted with permission from Noh et al.[54].
SMILES is a sequence-based text representation. Its power lies in the uniqueness of SMILES representation, namely, the standard SMILES representation can ensure that each chemical molecule has only one SMILES string, and it is a real language structure rather than just a computer data structure, which offers a natural advantage in using machine learning language models. For example, recurrent neural networks containing long short-term memory have been trained as generative models for molecules[45,55], which can generate valid SMILES strings with high accuracy. Gómez-Bombarelli et al.[19] reported a VAE model using SMILES to build multidimensional continuous molecule representation. Adversarial networks using SMILES representation are also investigated[56,57]. Because of its unique reversible mapping and clear meaning, SMILES has been most frequently applied in inverse molecular design[20,58,59].
In the molecular graph G = (V, E), atoms are represented as nodes vi∈V and chemical bonds as edges (vi, vj)∈E. Nodes and edges are assigned with labels according to the type of atoms and chemical bonds. Many attempts have been made to construct generative models with the graph representation of molecules.
Reversibility and symmetry invariance for the above representations of molecules come from the definite identification of chemical bonds, which determines the number of atomic connection (saturability) and orbital overlap direction (directivity). However, for inorganic solid materials, the chemical bonding is much more complicated. Therefore, saturability and directivity are often unsatisfied, leading to the failure of structure representation solely in terms of the connection between atoms. Although the crystal representation based on graph theory has been developed[63], it is not feasible to reconstruct the crystal structure from the graph, which restricts its application in generative models.
Periodicity is another critical issue for crystal representations. Properties of crystals depend not only on the atomic arrangement in the structure unit, but also on the periodic repetition of the unit in the space. This would raise a new problem that is difficult to deal with: there are various choices for selecting the cell when representing one crystal structure and different choices would lead to large or even unacceptable errors in encoding crystals with similar or identical structures. Such a question is still not fully resolved in recent inverse design studies.
Various general descriptors for solid materials based on specific tasks have been developed, and some related studies have summarized these descriptors[5,64-67]. For conventional machine learning tasks, a good representation should not only satisfy the key criteria, namely, uniqueness, universality, and efficiency[68], but also be explicitly tailored to specific subfields (e.g., batteries[64,69], catalysts[70], or photovoltaics[71]). For the tasks of inverse design via generative models, however, the reversibility, symmetry invariance, and periodicity mentioned above are also indispensable, although it is quite difficult to fulfill all criteria at the same time. Here, we list some of the representative structure encoding schemes that have been used for inverse design of inorganic solid materials.
Bag-of-atoms representation is one of the efforts to encode inorganic crystals [Figure 3B][51], which considers a single structure and is only designed for optimization of compositions. Some generative models use the lattice vector and atomic position matrix in the crystallographic information files (CIFs) for structure representation [Figure 3C]. For example, Nouira et al.[72] trained a GAN model to generate novel ternary metal hydrides from observed binary structures. Ren et al.[73] embedded solid-state physics knowledge to construct descriptors which combine both the real space and the momentum space, and display lower error in predicting the formation energy and bandgap. The real space matrix was primarily constructed by the lattice vectors and the atomic coordinates, while the momentum space matrix involved the representative crystal planes that describe symmetry and periodicity. Other works try to convert the atomic position matrix into the density matrix[53,74,75] [Figure 3D], where the locations of atoms can be reconstructed by augmenting the training dataset via rotating and expanding the single unit cell. In their work, an error of 0.5 Å in atomic position between the predicted and real structures was guaranteed for nearly 99% of the atoms. Another approach is to let the neural network learn the encoding requirements by itself. Noh et al.[54] developed a 3D image representation [Figure 3E], which was similar in essence to the density matrix representation but relies on Gaussian kernel distribution of atoms. We note that data augmentation is applicable to solve the problem of symmetry invariance to a certain extent, yet it would significantly increase the computational burden. Efficient representation of inorganic solid materials for generative models is still a direction that requires more exploration.
TASK OF INVERSE DESIGN
Current research of inverse design in materials science is mainly centered on two topics: compositional optimization and structure prediction. These correspond to the exploration of chemical space by focusing on the compositional and configurational degrees of freedom.
A prohibitive computational cost would be expected if we try to explore the whole compositional space. For a four-element compound, a survey of the first 103 elements of the periodic table would result in a total of 1012 different compounds through permutation and combination. The number would be reduced to 1010 if charge neutrality and electronegativity balance are taken into consideration[76]. In this case, generative models in machine learning can provide an affordable means to navigate the compositional space by implicitly learning the underlying chemical rules. Dan et al.[77] trained a GAN model with materials from the ICSD database, where two million chemical compositions were generated. Overall, 84.5% of the predicted materials are charge-neutral and electronegativity-balanced, even though there were no chemical rules explicitly enforced. It is worth noting that inverse design of compositions is not restricted to representation schemes for encoding the atomic structures; that is, features not containing any structural information could also be utilized as input. On the other hand, Nguyen et al.[78] developed a hybrid generative-discriminative model with partial phase diagram as the feature, which holds great promise for speeding up the compositional design of aluminum alloys by over 100,000 times.
As compared to compositional degrees of freedom in materials, the problem with configurational degrees of freedom is much more complex. Many challenges remain to be addressed for inverse design of crystal structures. Learning from the atomic positions in the training dataset, the generative models can estimate the probability of a specific atom occupying a certain position in the space. We highlight one such example, the image-based materials generator (iMatGen) framework designed by Noh et al.[54] The iMatGen first encodes the vanadium oxide CIFs into a 3D image and uses continuous representations as well as formation energies as inputs to the VAE for the construction of latent space for V-O binary compounds. By decoding the sampled points back to crystal structures, 26 out of the 31 previously known vanadium oxides were rediscovered, and over 40 entirely new V-O binary compounds with relatively high stability were generated.
It is generally anticipated that, for large spatial freedom, a huge training set would be needed to guarantee that the model can effectively learn the distribution laws of atoms in space. Court et al.[74] trained a VAE and UNet on 78,750 ternary perovskites, binary alloys, and Heusler compounds. The average mean absolute error (MAE) on validation dataset for the lattice parameters is as low as 0.06 Å, and the average earth-mover distance of atomic coordinates between encoding and decoding is 0.09 Å. In another work, 24,785 ternary compounds were screened from the MP database for VAE training[73]. The MAE for the atomic sites is 0.001, and the percentage mean absolute errors for the length of lattice constant and the lattice angle are 7.41% and 3.99%, respectively. After careful calculations for 27 predicted crystals, two of them exhibited power factors comparable to the best thermoelectric materials.
Given that crystals composed of the same elements often have similar structures, it is generally more feasible to train models with elemental constraints, which could reduce the reliance on large dataset. For metal organic frameworks[79], zeolites[75], and two-dimensional graphene/h-BN hybrids[80], the constituent elements are rather restricted, while there are a large amount of data for use in training the generative models. Nevertheless, a situation of high elemental diversity and low structural diversity is often encountered for inorganic materials datasets, which underlines the crucial role of element substitution[21,52,54], few-shot learning[73,81], and transfer learning[82,83] in tackling the inverse design tasks.
The inclusion of properties during the inverse design is still challenging, whether for the exploration of composition or structure. Generally, the constraints of the networks can only ensure that GAN and VAE can reconstruct materials with composition and structure close to the real materials. For an extremely large chemical space, the approach based on basic GAN or VAE are uncontrollable, and the predicted results could be meaningless. To solve the problem, the conditional generative models, such as conditional VAE[84] and conditional GAN[85], can be leveraged for material generation with desired properties
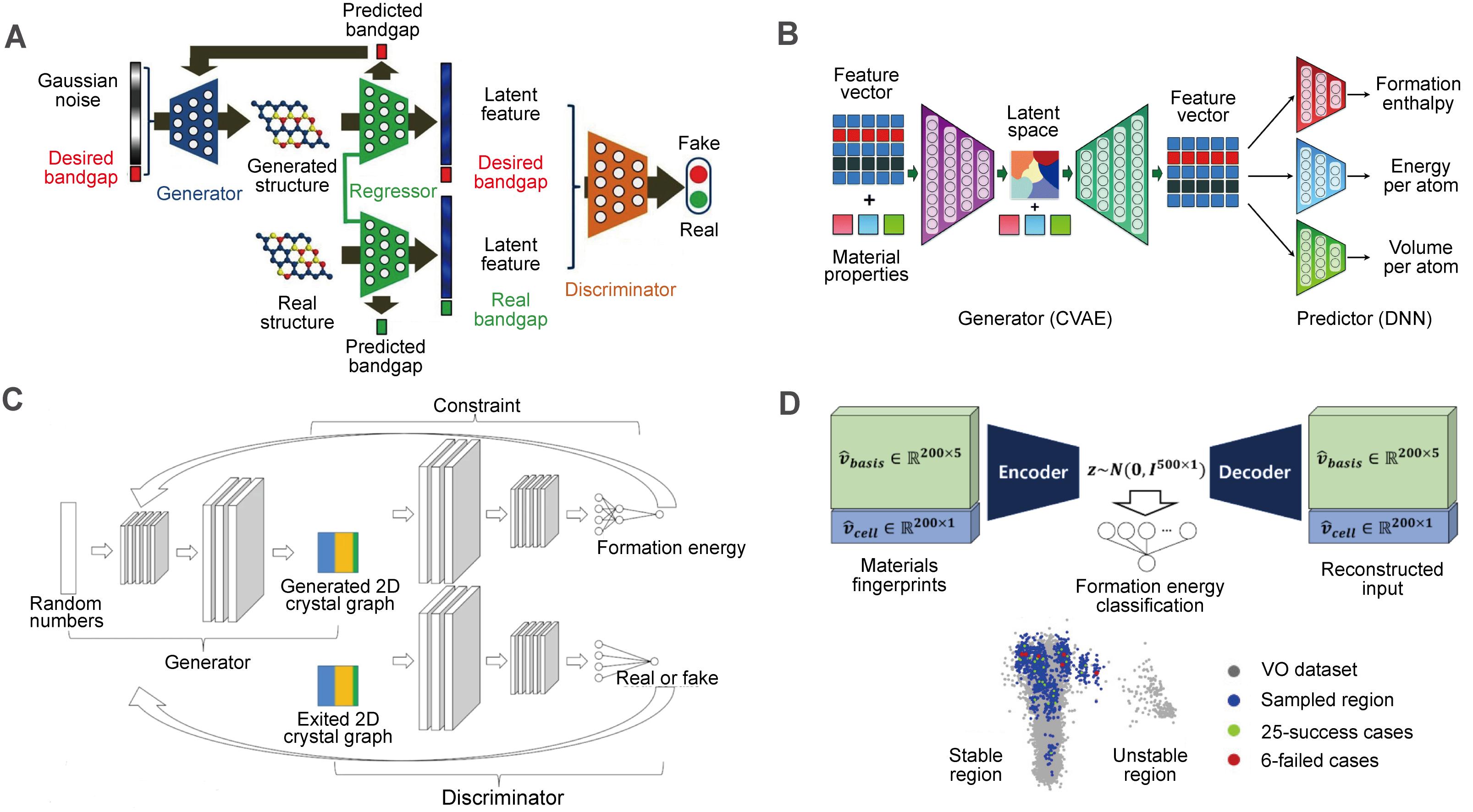
The conditional deep-feature-consistent VAE was constructed recently, which employed the electron-density maps as input and the formation energy per atom as condition[74]. Clustering effect related to the formation energy in latent space was shown. To perform both regressional and conditional tasks in GAN, Dong et al.[80] developed an improved CGAN called regressional and conditional GAN, which contains a regression convolution neural network between generator and discriminator to predict bandgap as well as output the latent features from material structures [Figure 4A]. In addition to the use of constraints in the generative model, Pathak et al.[51] suggested that additional predictive networks can be used to further filter materials with specific properties. They proposed a deep learning based inorganic material generator architecture consisting of a generator and a predictor [Figure 4B]. Long et al.[21] further integrated constraint network into GAN as a back propagator without embedding properties in input to realize automated optimization of generator and predictor. A constrained crystals deep convolutional GAN was thus established [Figure 4C], which is more efficient than traditional GAN in generating stable structures.
Figure 4. Networks for inverse design of inorganic solid materials. (A) Regressional and conditional GAN (RCGAN) framework. This figure is quoted with permission from Dong et al.[81]. (B) Deep learning based inorganic material generator (DING) framework consisting of a generator module and a predictor module. This figure is quoted with permission from Pathak et al.[51]. (C) Constrained crystals deep convolutional GAN (CCDCGAN) framework. This figure is quoted with permission from Long et al.[21]. (D) Materials generator module in iMatGen and the visualization of the latent space. This figure is quoted with permission from Noh et al.[54].
It is worth mentioning that, for GAN frameworks, in addition to the trouble of material representation mentioned above, another critical issue is that the training process of GAN can be very challenging to achieve convergence. The gradient disappearance[86] and mode collapse[87] could seriously hinder the application of GAN in material generation. Gradient disappearance means that, when the back propagation is used for neural network training, the gradient propagated to shallow network cannot give rise to numerical disturbance, which eventually leads to slow convergence or even fails to converge. Especially, an accurate discriminator is more likely to aggravate the issue of gradient disappearance[88]. Mode collapse refers to the situation that GAN cannot generate diversified materials; that is, only materials that strongly resemble or even belong to the real samples can be derived from the model. This issue is a great handicap to data augmentation tasks. The main reason for gradient disappearance and mode collapse in GAN training lies in that the Jensen-Shannon (JS) divergence is used to measure the distance between two distributions. One solution is to adopt Wasserstein GAN[89], which relies on Wasserstein distance instead of JS divergence and performs better when there is negligible overlap between both distributions. There are also variants such as Laplacian pyramid of GAN[90], boundary equilibrium GAN[91], and BigGAN[92], which differed in the cost function. Although the pros and cons of these models in image generation have been frequently discussed, the influence of cost functions is still an interesting topic in material generation.
It is worth mentioning that in the latent space of VAE, materials are represented as continuous and differentiable vectors, which is completely different from the way of generating materials with target property. To explore the unknown area in the latent space, a routine sampling strategy is to decode the random vector near the known material in the latent space. Apparently, the shape of the latent space and the sampling strategy will significantly affect the generation results. To enhance the sampling efficiency, iMatGen carried out a formation energy classification to latent vector. The crystals with formation energy greater than 0.5 eV/atom were regarded as stable materials[54], resulting in the separation of latent space into two regions [Figure 4D]. By executing the sampling strategy only in the stable region, the formation energy of vanadium oxides can be effectively constrained. Another effective approach to impose constraints when navigating in the latent space would be to train neural networks for property prediction from latent vector[19], after which the gradient optimization algorithm in the latent space could be applied.
Another noteworthy issue is the visualization of the latent space in VAE. In a standard visualization process, the encoder encodes high-dimensional material descriptors into low-dimensional latent vectors, and then dimension reduction algorithm is applied to map these vectors to two-dimensional space for visualization. Common dimensionality reduction algorithms include principal component analysis[93], multidimensional scaling[94], t-distributed stochastic neighbor embedding[95], sketch-map[96], etc. As the input of the dimensionality reduction algorithm is a latent vector without manual selection of features, we are incapable of predicting the final performance of dimensionality reduction in advance, and hence the choice of algorithms is generally subjected to the characteristics of the dataset.
The most critical step in forward design is experimental synthesis. In a recent study, a machine learning model was constructed to quantify the probability of synthesis for virtual materials[97], in which an 87.5% true positive prediction accuracy was attained. Actually, even if we know the synthesizability of the materials, it is still hoped that the condition for material synthesis can also be predicted. As far as we know, there is no generative model available in this research direction, whereas most of the previous studies have been done using optimization methods[98-100]. One possible challenge is to obtain sufficient experimental data with small error. The establishment of generative models to predict the experimental condition for material synthesis is still an open challenge.
OUTLOOK
Inverse design is an important path for rapid materials discovery in the future. With the development of high-throughput computation and material databases, data-driven generative models promise to be powerful tools for inverse materials design. Although generative models have begun to show promise in the field of inverse design for organic molecules, their application in inorganic solid materials is still in the infancy period. Here, we proceed by listing some of the critical issues that require consideration.
First, the performance of the generative model is dictated by the size and quality of the training set. Although high-throughput ab initio calculations can be applied for the generation of a portfolio of materials with element substitution, it is notoriously time-consuming when complicated structures are involved. We note that few-shot learning and transfer learning may improve the performance of inverse design of inorganic solid materials, but they are still far from satisfactory. For transfer learning, the inconsistent distribution of atomic positions in different types of crystals may be the key problem to be solved.
Secondly, the representation and encoding of inorganic solid materials could influence the sampling in latent space and the generation results. Periodicity is an important characteristic that inorganic solid materials differ from molecules. Relying solely on atomic coordinates and unit cell parameters as inputs of the material generation model is obviously not realistic. Although it can meet the requirements of reversibility, it cannot realize symmetry invariance and periodicity, in which case two cells representing the same crystal can be distinct from each other in latent space. This could jeopardize the predictive power of the model. To solve this problem, knowledge from mathematics and solid-state physics is indispensable[73].
Finally, generative networks themselves are an issue worth exploring. Currently, almost all results obtained from generation models are not directly usable and require post-processing, such as atomic trade-offs[54,75] and ab initio structural optimizations[52]. It is worth tackling how networks can be trained to produce materials that are usable with minimal optimization. In addition, reinforcement learning has been exercised in molecular generation[20,56,101]. It would be fruitful to evaluate its application in the generative models for inverse design of inorganic solid materials.
DECLARATIONS
Authors’ contributionsMade substantial contributions to conception and design of the study and performed data analysis and interpretation: Chen LT, Li SN, Pan F
Performed data acquisition: Chen LT, Zhang WT, Nie ZW
Performed administrative support: Pan F
Availability of data and materialsNot applicable.
Financial support and sponsorshipThis work was financially supported by the National Key R&D Program of China (2016YFB0700600, 2020YFB0704500), the Shenzhen Science and Technology Research Grant (No. JCYJ20200109140416788), and the Chemistry and Chemical Engineering Guangdong Laboratory (Grant No. 1922018).
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2021.
REFERENCES
1. Zunger A. Inverse design in search of materials with target functionalities. Nat Rev Chem 2018:2.
2. Sanchez-Lengeling B, Aspuru-Guzik A. Inverse molecular design using machine learning: generative models for matter engineering. Science 2018;361:360-5.
3. Butler KT, Davies DW, Cartwright H, Isayev O, Walsh A. Machine learning for molecular and materials science. Nature 2018;559:547-55.
4. Hong Y, Hou B, Jiang H, Zhang J. Machine learning and artificial neural network accelerated computational discoveries in materials science. WIREs Comput Mol Sci 2020:10.
5. Li S, Liu Y, Chen D, Jiang Y, Nie Z, Pan F. Encoding the atomic structure for machine learning in materials science. WIREs Comput Mol Sci 2021; doi: 10.1002/wcms.1558.
6. Tabor DP, Roch LM, Saikin SK, et al. Accelerating the discovery of materials for clean energy in the era of smart automation. Nat Rev Mater 2018;3:5-20.
7. Lilienfeld OA, Müller K, Tkatchenko A. Exploring chemical compound space with quantum-based machine learning. Nat Rev Chem 2020;4:347-58.
8. Nie Z, Liu Y, Yang L, Li S, Pan F. Construction and application of materials knowledge graph based on author disambiguation: revisiting the evolution of LiFePO4. Adv Energy Mater 2021;11:2003580.
9. Noh J, Gu GH, Kim S, Jung Y. Machine-enabled inverse design of inorganic solid materials: promises and challenges. Chem Sci 2020;11:4871-81.
11. Kim C, Pilania G, Ramprasad R. Machine learning assisted predictions of intrinsic dielectric breakdown strength of ABX3 perovskites. J Phys Chem C 2016;120:14575-80.
12. Furmanchuk A, Agrawal A, Choudhary A. Predictive analytics for crystalline materials: bulk modulus. RSC Adv 2016;6:95246-51.
13. Kauwe SK, Graser J, Vazquez A, Sparks TD. Machine learning prediction of heat capacity for solid inorganics. Integr Mater Manuf Innov 2018;7:43-51.
14. Li W, Jacobs R, Morgan D. Predicting the thermodynamic stability of perovskite oxides using machine learning models. Computational Materials Science 2018;150:454-63.
15. Zheng X, Zheng P, Zhang RZ. Machine learning material properties from the periodic table using convolutional neural networks. Chem Sci 2018;9:8426-32.
16. Raccuglia P, Elbert KC, Adler PD, et al. Machine-learning-assisted materials discovery using failed experiments. Nature 2016;533:73-6.
17. Weston L, Tshitoyan V, Dagdelen J, et al. Named entity recognition and normalization applied to large-scale information extraction from the materials science literature. J Chem Inf Model 2019;59:3692-702.
18. Tshitoyan V, Dagdelen J, Weston L, et al. Unsupervised word embeddings capture latent knowledge from materials science literature. Nature 2019;571:95-8.
19. Gómez-Bombarelli R, Wei JN, Duvenaud D, et al. Automatic chemical design using a data-driven continuous representation of molecules. ACS Cent Sci 2018;4:268-76.
20. Popova M, Isayev O, Tropsha A. Deep reinforcement learning for de novo drug design. Sci Adv 2018;4:eaap7885.
21. Long T, Fortunato NM, Opahle I, et al. Constrained crystals deep convolutional generative adversarial network for the inverse design of crystal structures. npj Comput Mater 2021:7.
22. Kingma DP, Welling M. Auto-encoding variational bayes. Available from: https://arxiv.org/abs/1312.6114 [Last accessed on 13 Sep 2021].
23. Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets. Available from: https://papers.nips.cc/paper/2014/file/5ca3e9b122f61f8f06494c97b1afccf3-Paper.pdf [Last accessed on 13 Sep 2021].
24. Davies DW, Butler KT, Skelton JM, Xie C, Oganov AR, Walsh A. Computer-aided design of metal chalcohalide semiconductors: from chemical composition to crystal structure. Chem Sci 2018;9:1022-30.
25. Zakutayev A, Zhang X, Nagaraja A, et al. Theoretical prediction and experimental realization of new stable inorganic materials using the inverse design approach. J Am Chem Soc 2013;135:10048-54.
26. Acosta CM, Fazzio A, Dalpian GM, Zunger A. Inverse design of compounds that have simultaneously ferroelectric and Rashba cofunctionality. Phys Rev B 2020:102.
27. Noh J, Kim S, Gu GH, et al. Unveiling new stable manganese based photoanode materials via theoretical high-throughput screening and experiments. Chem Commun (Camb) 2019;55:13418-21.
28. Lazauskas T, Sokol AA, Woodley SM. An efficient genetic algorithm for structure prediction at the nanoscale. Nanoscale 2017;9:3850-64.
29. Alberi K, Nardelli MB, Zakutayev A, et al. The 2019 materials by design roadmap. J Phys D Appl Phys 2018;52:013001.
30. Bergerhoff G, Hundt R, Sievers R, Brown ID. The inorganic crystal structure data base. J Chem Inf Comput Sci 1983;23:66-9.
31. Kirklin S, Saal JE, Meredig B, et al. The Open Quantum Materials Database (OQMD): assessing the accuracy of DFT formation energies. npj Comput Mater 2015:1.
32. Jain A, Ong SP, Hautier G, et al. Commentary: the materials project: a materials genome approach to accelerating materials innovation. APL Materials 2013;1:011002.
33. Meredig B, Agrawal A, Kirklin S, et al. Combinatorial screening for new materials in unconstrained composition space with machine learning. Phys Rev B 2014:89.
34. Regmi K, Borji A. Cross-view image synthesis using geometry-guided conditional GANs. Computer Vision and Image Understanding 2019;187:102788.
35. Cao J, Hu Y, Yu B, He R, Sun Z. 3D aided duet GANs for multi-view face image synthesis. IEEE Trans Inform Forensic Secur 2019;14:2028-42.
38. Cha M, Gwon YL, Kung HT. Adversarial learning of semantic relevance in text to image synthesis. AAAI 2019;33:3272-9.
40. Wang TC, Liu MY, Tao A, Liu G, Kautz J, Catanzaro B. .
41. Kumar K, Kumar R, de Boissiere T, et al. .
42. Donahue C, McAuley J, Puckette M. .
43. Bińkowski M, Donahue J, Dieleman S, et al. .
44. Blaschke T, Olivecrona M, Engkvist O, Bajorath J, Chen H. Application of generative autoencoder in de novo molecular design. Mol Inform 2018;37:1700123.
45. Segler MHS, Kogej T, Tyrchan C, Waller MP. Generating focused molecule libraries for drug discovery with recurrent neural networks. ACS Cent Sci 2018;4:120-31.
46. Kadurin A, Nikolenko S, Khrabrov K, Aliper A, Zhavoronkov A. druGAN: an advanced generative adversarial autoencoder model for de novo generation of new molecules with desired molecular properties in silico. Mol Pharm 2017;14:3098-104.
47. Kadurin A, Aliper A, Kazennov A, et al. The cornucopia of meaningful leads: Applying deep adversarial autoencoders for new molecule development in oncology. Oncotarget 2017;8:10883-90.
48. Weininger D, Weininger A, Weininger JL. SMILES. 2. Algorithm for generation of unique SMILES notation. J Chem Inf Comput Sci 1989;29:97-101.
49. Weininger D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J Chem Inf Model 1988;28:31-6.
50. Kearnes S, McCloskey K, Berndl M, Pande V, Riley P. Molecular graph convolutions: moving beyond fingerprints. J Comput Aided Mol Des 2016;30:595-608.
51. Pathak Y, Juneja KS, Varma G, Ehara M, Priyakumar UD. Deep learning enabled inorganic material generator. Phys Chem Chem Phys 2020;22:26935-43.
52. Kim S, Noh J, Gu GH, Aspuru-Guzik A, Jung Y. Generative adversarial networks for crystal structure prediction. ACS Cent Sci 2020;6:1412-20.
53. Hoffmann J, Maestrati L, Sawada Y, Tang J, Sellier JM, Bengio Y. Data-driven approach to encoding and decoding 3-D crystal structures. Available from: https://arxiv.org/abs/1909.00949 [Last accessed on 13 Sep 2021].
54. Noh J, Kim J, Stein HS, et al. Inverse design of solid-state materials via a continuous representation. Matter 2019;1:1370-84.
55. Gupta A, Müller AT, Huisman BJH, Fuchs JA, Schneider P, Schneider G. Generative recurrent networks for de novo drug design. Mol Inform 2018;37:1700111.
56. Guimaraes GL, Sánchez-Lengeling B, Farias PLC, Aspuru-Guzik AJA. Objective-reinforced generative adversarial networks (ORGAN) for sequence generation models. Available from: https://arxiv.org/abs/1705.10843 [Last accessed on 13 Sep 2021].
57. Sanchez B, Outeiral C, Guimaraes G, Aspuru-Guzik A. Optimizing distributions over molecular space. An objective-reinforced generative adversarial network for inverse-design chemistry (ORGANIC). ChemRxiv. Cambridge: Cambridge Open Engage; 2017.
58. Lim J, Ryu S, Kim JW, Kim WY. Molecular generative model based on conditional variational autoencoder for de novo molecular design. J Cheminform 2018;10:31.
59. Prykhodko O, Johansson SV, Kotsias PC, et al. A de novo molecular generation method using latent vector based generative adversarial network. J Cheminform 2019;11:74.
60. Li Y, Zhang L, Liu Z. Multi-objective de novo drug design with conditional graph generative model. J Cheminform 2018;10:33.
61. Li Y, Vinyals O, Dyer C, Pascanu R, Battaglia P. Learning deep generative models of graphs. Available from: https://arxiv.org/abs/1803.03324 [Last accessed on 13 Sep 2021].
62. Simonovsky M, Komodakis N. GraphVAE: towards generation of small graphs using variational autoencoders. In: Kůrková V, Manolopoulos Y, Hammer B, Iliadis L, Maglogiannis I, editors. Artificial Neural Networks and Machine Learning - ICANN 2018. Cham: Springer International Publishing; 2018. p. 412-22.
63. Weng M, Wang Z, Qian G, et al. Identify crystal structures by a new paradigm based on graph theory for building materials big data. Sci China Chem 2019;62:982-6.
64. Zhao Q, Zhang L, He B, et al. Identifying descriptors for Li+ conduction in cubic Li-argyrodites via hierarchically encoding crystal structure and inferring causality. Energy Storage Materials 2021;40:386-93.
65. Keith JA, Vassilev-Galindo V, Cheng B, et al. Combining machine learning and computational chemistry for predictive insights into chemical systems. Chem Rev 2021;121:9816-72.
66. Liu Y, Zhao T, Ju W, Shi S. Materials discovery and design using machine learning. Journal of Materiomics 2017;3:159-77.
67. Chen C, Zuo Y, Ye W, Li X, Deng Z, Ong SP. A critical review of machine learning of energy materials. Adv Energy Mater 2020;10:1903242.
68. Lu Z. Computational discovery of energy materials in the era of big data and machine learning: a critical review. Materials Reports: Energy 2021;1:100047.
69. Zhao Q, Avdeev M, Chen L, Shi S. Machine learning prediction of activation energy in cubic Li-argyrodites with hierarchically encoding crystal structure-based (HECS) descriptors. Science Bulletin 2021;66:1401-8.
70. Gu GH, Choi C, Lee Y, et al. Progress in computational and machine-learning methods for heterogeneous small-molecule activation. Adv Mater 2020;32:e1907865.
71. Lu S, Zhou Q, Ouyang Y, Guo Y, Li Q, Wang J. Accelerated discovery of stable lead-free hybrid organic-inorganic perovskites via machine learning. Nat Commun 2018;9:3405.
72. Nouira A, Sokolovska N, Crivello JC. CrystalGAN: learning to discover crystallographic structures with generative adversarial networks. Available from: https://arxiv.org/abs/1810.11203 [Last accessed on 13 Sep 2021].
73. Ren Z, Noh J, Tian S, et al. Inverse design of crystals using generalized invertible crystallographic representation. Available from: https://arxiv.org/abs/2005.07609 [Last accessed on 13 Sep 2021].
74. Court CJ, Yildirim B, Jain A, Cole JM. 3-D inorganic crystal structure generation and property prediction via representation learning. J Chem Inf Model 2020;60:4518-35.
75. Kim B, Lee S, Kim J. Inverse design of porous materials using artificial neural networks. Sci Adv 2020;6:eaax9324.
76. Davies DW, Butler KT, Jackson AJ, et al. Computational screening of all stoichiometric inorganic materials. Chem 2016;1:617-27.
77. Dan Y, Zhao Y, Li X, Li S, Hu M, Hu J. Generative adversarial networks (GAN) based efficient sampling of chemical composition space for inverse design of inorganic materials. npj Comput Mater 2020:6.
78. Nguyen P, Tran T, Gupta S, Rana S, Venkatesh S. Hybrid Generative-Discriminative Models for inverse materials design. Available from: https://arxiv.org/abs/1811.06060 [Last accessed on 13 Sep 2021].
79. Yao Z, Sánchez-lengeling B, Bobbitt NS, et al. Inverse design of nanoporous crystalline reticular materials with deep generative models. Nat Mach Intell 2021;3:76-86.
80. Dong Y, Li D, Zhang C, et al. Inverse design of two-dimensional graphene/h-BN hybrids by a regressional and conditional GAN. Carbon 2020;169:9-16.
81. Wang Y, Yao Q, Kwok JT, Ni LM. Generalizing from a few examples: a survey on few-shot learning. ACM Comput Surv 2020;53:1-34.
83. Yamada H, Liu C, Wu S, et al. Predicting materials properties with little data using shotgun transfer learning. ACS Cent Sci 2019;5:1717-30.
84. Sohn K, Lee H, Yan X. Learning structured output representation using deep conditional generative models. In: Cortes C, Lawrence N, Lee D, Sugiyama M, Garnett R, editors. NIPS: Curran Associates, Inc; 2015.
85. Mirza M, Osindero S. Conditional generative adversarial nets. Available from: https://arxiv.org/abs/1411.1784 [Last accessed on 13 Sep 2021].
86. Hochreiter S, Bengio Y, Frasconi P, Schmidhuber J. Gradient flow in recurrent nets: the difficulty of learning long-term dependencies. A field guide to dynamical recurrent neural networks. IEEE Press;2001. p. 237-43.
87. Kodali N, Abernethy J, Hays J, Kira Z. On convergence and stability of GANs. Available from: https://arxiv.org/abs/1705.07215 [Last accessed on 13 Sep 2021].
89. Arjovsky M, Chintala S, Bottou L. .
90. Denton E, Chintala S, Szlam A, Fergus R. Deep generative image models using a laplacian pyramid of adversarial networks. Available from: https://arxiv.org/abs/1506.05751 [Last accessed on 13 Sep 2021].
91. Berthelot D, Schumm T, Metz L. BEGAN: boundary equilibrium generative adversarial networks. Available from: https://arxiv.org/abs/1703.10717 [Last accessed on 13 Sep 2021].
92. Brock A, Donahue J, Simonyan K. .
93. Jolliffe I. Principal Component Analysis. In: Lovric M, editor. International encyclopedia of statistical science. Berlin, Heidelberg: Springer Berlin Heidelberg; 2011, p. 1094-6.
94. Borg I. Multidimensional Scaling. In: Lovric M, editor. International encyclopedia of statistical science. Berlin, Heidelberg: Springer Berlin Heidelberg; 2011, p. 875-8.
95. Maaten LVD, Hinton GE. Visualizing data using t-SNE. Journal of Machine Learning Research 2008;9:2579-605.
96. Ceriotti M, Tribello GA, Parrinello M. From the Cover: Simplifying the representation of complex free-energy landscapes using sketch-map. Proc Natl Acad Sci U S A 2011;108:13023-8.
97. Jang J, Gu GH, Noh J, Kim J, Jung Y. Structure-based synthesizability prediction of crystals using partially supervised learning. J Am Chem Soc 2020;142:18836-43.
98. Jung J, Yoon JI, Park S, et al. Modelling feasibility constraints for materials design: Application to inverse crystallographic texture problem. Computational Materials Science 2019;156:361-7.
99. Johnson L, Arróyave R. An inverse design framework for prescribing precipitation heat treatments from a target microstructure. Materials & Design 2016;107:7-17.
100. Wang S, Jia Z, Lu X, Zhang H, Zhang C, Liang SY. Simultaneous optimization of fixture and cutting parameters of thin-walled workpieces based on particle swarm optimization algorithm. SIMULATION 2017;94:67-76.
Cite This Article
How to Cite
Chen, L.; Zhang, W.; Nie, Z.; Li, S.; Pan, F. Generative models for inverse design of inorganic solid materials. J. Mater. Inf. 2021, 1, 4. http://dx.doi.org/10.20517/jmi.2021.07
Download Citation
Export Citation File:
Type of Import
Tips on Downloading Citation
Citation Manager File Format
Type of Import
Direct Import: When the Direct Import option is selected (the default state), a dialogue box will give you the option to Save or Open the downloaded citation data. Choosing Open will either launch your citation manager or give you a choice of applications with which to use the metadata. The Save option saves the file locally for later use.
Indirect Import: When the Indirect Import option is selected, the metadata is displayed and may be copied and pasted as needed.
























Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.