Journal of Materials Informatics
Views: Downloads:
Views: Downloads:
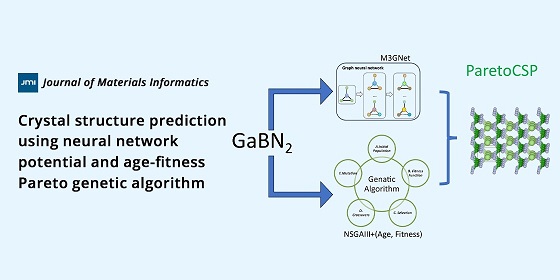
Crystal structure prediction using neural network potential and age-fitness Pareto genetic algorithm
Views: Downloads:
Views: Downloads:
Views: Downloads:
Views: Downloads:
Views: Downloads:
Views: Downloads:
Data
316
Authors
261
Reviewers
2021
Published Since
100,743
Article Views
39,702
Article Downloads
For Reviewers
For Readers
Add your e-mail address to receive forthcoming Issues of this journal:
Themed Collections
Related Journals
Related Journals
Data
316
Authors
261
Reviewers
2021
Published Since
100,743
Article Views
39,702
Article Downloads