CuB monolayer: a novel 2D anti-van't Hoff/Le Bel nanostructure with planar hyper-coordinate boron/copper and superconductivity
Abstract
To achieve specific applications, it is always desirable to design new materials with peculiar topological properties. Herein, based on a D2h B2Cu6H6 molecule with the unique chemical bonding of planar pentacoordinate boron (ppB) as a building block, we constructed an infinite CuB monolayer by linking B2Cu6 subunits in an orthorhombic lattice. The planarity of the CuB sheet is attributed to the multicenter bonds and electron donation-back donation, as revealed by chemical bonding analysis. As a global minimum confirmed by the particle swarm optimization method, the CuB monolayer is expected to be highly stable, as indicated by its rather high cohesive energy, absence of soft phonon modes, and good resistance to high temperature, and thus is highly feasible for experimental realization. Remarkably, this CuB monolayer is metallic and predicted to be superconducting with an estimated critical temperature (Tc) of 4.6 K, and the critical temperature could be further enhanced by tensile strains (to 21 K at atmospheric pressure).
Keywords
INTRODUCTION
The discovery of molecules and materials with unique bonding characteristics is highly desirable to advance materials science from the perspective of both fundamental understanding and applications. With various exceptional properties, such as its electron deficiency, small covalent radius, and versatility in adopting sp2 and sp3 hybridization, as well as multi-center bonds, boron can form plenty of polymorphs with intriguing chemical bonding[1-8]. Various nanostructures of boron, such as boron fullerenes[6-9], two-dimensional (2D) sheets[2,4,5,10,11], nanotubes[3-12], and core-shell structures[13,14], have been extensively studied. Excitingly, by joint theoretical and experimental efforts, Piazza et al. discovered the highly stable quasi-planar B36 cluster with a central hexagonal hole, providing the first evidence of the viability of single-atom layer boron sheets with hexagonal vacancies[15]. Notably, the recent fabrication of borophene monolayer[16-19] further elaborated the richness of boron chemistry and added a new member to the two-dimensional materials family[20-23]. With these structural diversities and concomitant fascinating properties, boron has been intensively employed to design new functional materials[16,24-26]. Moreover, a series of molecular wheels and 2D frameworks with unprecedented highly coordinated central transitional metal atoms have been either experimentally characterized or theoretically designed[27-30], which not only offers new methods to effectively modulate the structures and properties of boron polymorphs but also expands the frontier of boron chemistry. In organic chemistry, a well-known classical chemical model is the van’t Hoff/Le Bel rule, following which a tetracoordinate carbon is of tetrahedral configuration[31,32], and thus a molecule containing tetracoordinate carbon in non-tetrahedral coordination is called anti-van’t Hoff/Le Bel. However, nowadays, molecules or materials with planar hypercoordinate (higher than three) motifs[33,34] are generally considered as anti-van’t Hoff/Le Bel structures. Note that most of the planar molecules or 2D nanomaterials mentioned above consist of anti-van’t Hoff/Le Bel motifs, a special feature we address in this work.
Copper, an earth-abundant element, also forms various nanostructures. Among others, copper clusters have been extensively studied as building blocks of various organic and inorganic systems[35-38], and their catalytic activities have received great attention[39]; one-dimensional copper nanostructures (especially nanowires and nanorods) have shown great promise in various applications, such as in next-generation flexible and wearable electronics, functional electrodes, solar cells, and field emission devices[40]. Very recently, the yet-hypothetical free-standing 2D copper monolayer was predicted by Yang et al., which adopts the hexagonal close-packed structure in the energetically most favorable configuration[41].
Copper can also form alloy structures with unique chemical bonding and novel properties. For example, Yang and coworkers predicted the Cu2Si monolayer featuring planar hexacoordinated silicon and copper[42], which was shortly synthesized and exhibited 2D Dirac nodal line fermions[43], and its superconductivity was predicted[44]. Moreover, recent theoretical studies predicted that quasi-planar Cu2Te layers are 2D topological insulators[45], and the planar Cu2Ge monolayer is a diamagnetic metal[46].
At the molecular scale, Li et al. thoroughly investigated planar tetracoordinate[47] and pentacoordinate[48] B embedded in hydrocopper complexes. Especially, D5h Cu5H5B- cluster showed high stability due to the optimal size match between pentagon Cu5H5 and B atom. These findings suggest that copper and boron platforms together might trigger novel topology and properties. In this respect, Jia et al. theoretically predicted that the CuB monolayer with planar hypercoordinate boron/copper is the lowest-energy configuration in the 2D space, and this metallic monolayer is a promising electrocatalyst for CO reduction to ethanol[49]. Zhou et al. investigated 2D copper borides by ab initio evolutionary searches[50], discovered three new metastable monolayer structures (Cu7B15, CuB3, and CuB6), and found the CuB monolayer as predicted by Jia et al. in the potential energy surface[49]. Excitingly, Zhou’s group experimentally synthesized the C8B14 monolayer on the Cu(111) surface under an ultrahigh vacuum and revealed that the charge transfer between Cu and B atoms plays an important role in stabilizing the 2D monolayer[51].
Inspired by the above exciting findings, we carried out a deep study of 2D CuB alloys using first-principles calculations combined with a global minimum search. Our systematic computations showed that the lowest-energy configuration of the copper boride (CuB) nanosheets possesses highly ordered anti-van’t Hoff/Le Bel B2@Cu6 subunits (@ indicates that a B2 unit is embedded in the Cu6 ring) and has a fascinating chemical bonding with both planar heptacoordinate copper and planar pentacoordinate boron (ppB). The planar morphology of CuB monolayer mainly comes from its multicenter bonding characteristics and electron-donation-back-donation interactions. As a global minimum in 2D space, the CuB monolayer not only has remarkable mechanical properties but also is predicted to be a phonon-mediated superconductor with an estimated critical temperature (Tc) of 10 K. With large cohesive energy, kinetic stability, and high melting temperature, the newly predicted CuB monolayer has good potential for experimental realization.
COMPUTATIONAL METHODS
For the Cu6B2H6 molecule, full geometry optimization, electronic structure computations, and harmonic frequency analysis were carried out at the B3LYP/6-311+G(d,p)[52-54] level of theory utilizing the ORCA 4.0 program[55].
For the 2D CuB monolayer, density functional theory (DFT) computations were performed using the projector augmented wave (PAW) method[56,57] as implemented in the Vienna ab initio simulation package (VASP) code[58]. The Perdew-Burke-Ernzerhof exchange-correlation functional (PBE)[59] and a 600 eV energy cut-off were adopted. The geometric structures were fully optimized until the energy precision reached 10-6 eV and the atomic force was less than 10-3 eV/Å. During structure optimizations, the vacuum regions between layers were fixed to 15 Å to well separate the periodic images in the z-direction, whereas the x and y lattice vectors were fully relaxed. The Brillouin zone was sampled with a 10 × 8 × 1 Г-centered Monkhorst-Pack k-point grid for geometry optimizations, while a larger grid (30 × 24 × 1) was used for self-consistent calculations. Since PBE tends to underestimate the band gaps, the screened hybrid Heyd–Scuseria–Ernzerhof functional (HSE06)[60], which typically gives more accurate band gap values, was used to increase the reliability of the electronic structure predictions.
To better understand the unique bonding and stabilizing mechanism in the CuB monolayer, we carefully examined the chemical bonding via deformation charge density (DCD) analysis, electron localization function (ELF)[61,62] analysis, and the solid state adaptive natural density partitioning (SSAdNDP)[63] method. On the fly, pseudopotentials, as implemented in the CASTEP code[64], were used to calculate the bond overlap population (BOP)[65] values.
To assess the mechanical properties of the CuB nanosheet, the elastic constants were calculated, and based on the obtained elastic modulus tensors, the in-plane Young’s modulus and the Poisson’s ratio were evaluated.
To evaluate the kinetic stability of 2D CuB structures, we performed phonon dispersion calculations based on the density functional perturbation theory (DFPT)[66] using the Phonopy code interfaced with VASP. During the phonon calculations, more stringent energy and force convergence criteria (10-8 eV and
To assess the thermal stabilities of the 2D CuB monolayer, using the PAW method and PBE functional, we performed ab initio molecular dynamics (AIMD) simulations in the canonical NVT ensemble. In these AIMD simulations, the initial configurations of CuB monolayer with 3 × 2 supercell (24 Cu atoms and 24 B atoms) were annealed at different temperatures (300, 600, 900, 1200, and 1500 K, respectively), each MD simulation lasted for 15 ps (at a time step of 1.0 fs), and the temperature was controlled by using the Nosé–Hoover thermostat[67].
The particle swarm optimization (PSO) method, as implemented in the CALYPSO code, was employed for searching low-lying 2D CuB monolayers. In these calculations, the simulation cells containing total atoms of 2, 4, 6, and 8 were considered, and the population size and the number of generations were set to 30 and 50, respectively. The structural relaxations were performed at the PBE level of theory using the VASP code.
Using the Quantum Espresso (QE) package[68], we computed the phonon dispersion and the electron-phonon coupling (ECP) to investigate the phonon-mediated superconducting properties and estimate the superconducting critical temperature (Tc) of the 2D CuB monolayers (including those under external strains). In these calculations, the plane wave ultrasoft pseudopotentials and the LDA functional for exchange–correlation interaction were used to model the electron–ion interactions[69,70], and the VASP structures were re-optimized within QE. The kinetic energy cut-off and the charge density cut-off of the plane wave basis were chosen as 90 and 900 Ry, respectively. The self-consistent calculations were carried out using a 32 × 32 × 1 Monkhorst-Pack k-point mesh. The full Brillouin zone phonon spectra were calculated from the dynamical matrices and EPC matrix elements on a 4 × 4 × 1 q-point grid. The Tc values were estimated based on the McMillan-Allen-Dynes formula.
RESULTS AND DISCUSSION
Cu6B2H6 as the inspiring ppB species for 2D monolayer
Our design of the periodic 2D CuB monolayer was inspired by the Cu6B2H6 molecule, which contains planar penta-coordinated boron (ppB) motifs. Cu6B2H6 has a singlet ground state with D2h symmetry [Figure 1A]. At the B3LYP/6-31+G* level of theory, Cu6B2H6 is a local minimum with the lowest vibrational frequency of 66.1 cm-1. In this molecule, the center B atom binds with four peripheral Cu atoms and its adjacent B atom, leading to the formation of ppB species. The distances between the ppB atom and Cu atoms (2.03 and
Figure 1. (A) Top and side views of the optimized structure of Cu6B2H6 molecule. The blue, green, and white balls represent Cu, B, and H atoms, respectively. The bond lengths (in Å) of the representative chemical bonds are given in black. (B) The canonical molecular orbitals of Cu6B2H6 molecule.
To gain further insights into the bonding features of Cu6B2H6, we calculated the atomic charges and the Wiberg bond index (WBI)[76-78] by natural bonding orbital (NBO) computations[79,80] at the B3LYP/6-311+G(d,p) level of theory. Since D5h BH5 is isoelectronic to D4h CH4[81], the pentacoordinate B can also be stabilized by σ donation group or delocalization of B pz electrons, as in the case of tetracoordinate carbon. Based on the charges obtained by natural population analysis (NPA)[82], the natural electron configuration of ppB is 2s0.832px1.072py0.892pz0.88, and the center B atoms gains 0.70 |e| from neighboring Cu atoms, which donates 0.21 and 0.60 |e|, respectively, while H atoms play as charge compensate group. The WBIs for ppB-Cu bonds are 0.38 and 0.40, respectively, whereas the WBI for ppB-ppB bond is 1.92, which indicates that the partial bonds are formed between ppB and its adjacent Cu atoms, while the B-B interactions have double-bond characteristics. These give the ppB center a total WBI of 3.92.
Additionally, we examined the canonical molecular orbitals of the Cu6B2H6 molecule to better understand its stabilization mechanism. As shown in Figure 1B, the central B atom and the surrounding Cu atoms are involved in the highly delocalized π (HOMO, HOMO-13, and HOMO-27) and σ (HOMO-1, HOMO-2, HOMO-22, HOMO-24, HOMO-31, and HOMO-32) orbitals; thus, it is these well-delocalized electrons that help retain the B center and peripheral Cu atoms in the same plane. Especially, the electron donation from the central B atoms to the surrounding Cu atoms (HOMO-1) and back-donation from the peripheral Cu atoms to the embedded B atoms (HOMO) play an important role in stabilizing ppB in the Cu6B2H6 molecule.
Geometric structure of the CuB monolayer
The exceptional chemical bonding of the ppB containing Cu6B2H6 inspired us to design a new 2D planar structure, namely CuB monolayer. The CuB monolayer has a highly symmetric structure with an orthorhombic lattice with space group Cmmm (No. 65) [Figure 2A]. The unit cell of the CuB monolayer consists of four B and four Cu atoms, and the optimized lattice parameters are a = 4.84 Å and b = 6.16 Å, respectively. Similar to the Cu6B2H6 molecule, each B atom in the CuB monolayer binds with the four nearest Cu atoms and one adjacent B atom, forming a B2@Cu6 subunit in the same plane. In the meantime, one Cu atom is shared by three B2@Cu6 subunits with a heptacoordination environment, including three Cu atoms and four B atoms. In the CuB monolayer, the Cu-B bond lengths (2.05 and 2.01 Å) are quite close to those of the Cu6B2H6 molecule, whereas the B-B bond length (1.64 Å) deviates a little from that of Cu6B2H6 molecule, but it is comparable to that in borophene (1.65–1.87 Å)[25,26].
Figure 2. (A) Top and side views of the optimized structure of the CuB monolayer. The black dashed lines denote a unit cell; a and b represent the lattice vectors; and orange-filled hexagons are guidelines for the B2@Cu6 subunit. (B) The deformation charge density of CuB monolayer. Cyan and yellow represent electron-deficient and -rich regions, respectively. The isosurface value is 0.01 e/au.
To elucidate the unique bonding nature and stabilizing mechanism in the CuB monolayer, we plotted the deformation charge density (DCD), which was obtained by subtracting the charge density of isolated Cu and B atoms within the CuB monolayer [Figure 2B]. There is significant electron transfer from the 4s orbital of Cu atoms to B atoms, and the transferred electrons are delocalized inside the B2@Cu6 subunits, contributing to the stabilization of the copper boride systems. According to Hirschfeld population analysis[83], each Cu atom transfers 0.20 e to the nearby B atoms, suggesting the considerable ionization of Cu atoms. We further performed the bond overlap population (BOP) analysis to investigate the nature of chemical bonding. Note that a high BOP value denotes a larger covalency, while a low BOP value indicates a stronger ionicity. The B-B bonds have large BOP values (1.39), indicating a strong covalent bonding interaction. The BOP value of Cu-B bonds (0.43) is moderate, indicating a partial ionic and partial covalent bond interaction.
The electron localization function (ELF) provides a (local) measure of electron localization in molecules and solids and is a widely used tool for chemical bond classification and for understanding atomic structures. The ELF ranges from 0 to 1, where regions close to 0 represent very low charge density, the regions close to 1 correspond to perfect localization or denote strongly covalent bonding electrons, and the regions with 0.5 characterize a homogeneous electron gas. In the CuB monolayer, the electrons are well localized on B-B and Cu-B bonds [Figure 3], indicating the dominant covalent interactions inside each B2@Cu6 subunit, which is consistent with DCD analysis. While the electrons are well delocalized around Cu atoms, the whole Cu frameworks are in the color corresponding to the values around 0.44, implying the robust connection between Cu atoms, which is vital to electronically stabilize these 2D Cu-B networks. This electron transfer mechanism helps to stabilize the 2D copper boride systems. Moreover, the synergetic electron donation and back-donation interactions between the Cu and B atoms, as revealed in the Cu6B2H6 molecule, contribute to the stabilization of the ppB configuration in the CuB monolayer.
Figure 3. (A) Isosurface of electron localization function plotted with the value of 0.5 au and (B) ELF maps sliced perpendicular to (001) direction of CuB monolayer. In the ELF maps, the red and blue colors refer to the highest value (0.88) and the lowest value (0.00) of ELF, indicating electron accumulation and depletion in different colored regions, respectively.
Note that our newly constructed CuB monolayer inspired by the ppB containing Cu6B2H6 molecule is the same Cu-B monolayer as recently predicted by Jia et al., and our ELF analysis also agrees well with their finding[49].
We further analyzed the chemical bonding pattern of the CuB monolayer using the SSAdNDP method, which can interpret chemical bonding in terms of classical lone pairs and two-center bonds, as well as multicenter delocalized bonds[63]. Figure 4 presents the vital multicenter chemical bonding. Each unit cell of the CuB monolayer contains 12 lone pairs of d-type electrons on four Cu atoms, eight three-center-two-electron (3c-2e) Cu-B-Cu σ bonds, six 8c-2e B2@Cu6 σ bonds, and two 8c-2e B2@Cu6 π bonds, accounting for 56 valence electrons per unit cell. The reckoned bonding figure is consistent with the symmetry of the CuB monolayer. Hence, the abundance of multicenter delocalized σ and π bonds endows the CuB monolayer with high stability and planarity.
Stability of the CuB monolayer
We first evaluated the thermodynamic stability (by computing its cohesive energy) and kinetic stability (by examining its phonon dispersion along the high-symmetry lines in the first Brillouin zone). The obtained results are essentially the same as those reported by Jia et al.[49]; thus, they are not discussed here.
We then assessed the thermal stability of the CuB monolayer. Throughout 15 ps AIMD simulations up to 1200 K, the framework of the CuB sheet is well kept in its original configuration, and the B2@Cu6 subunits only have slight out-of-plane distortions [Figure 5A and B]. However, the B2@Cu6 subunits break at an extremely high temperature of 1500 K where B tends to form a chain structure [Figure 5C]. The well-maintained geometries at the high temperature up to 1200 K indicate the high thermal stability of the CuB monolayer. Additionally, we performed simulated annealing from the distorted structures obtained by AIMD at 900 and 1200 K, and these distorted structures can easily recover to their initial configurations, indicating the high phase stability of the CuB monolayer.
Figure 5. A snapshot of equilibrium structure of CuB monolayer at the end of 15 ps ab initio molecular dynamics simulations at different temperatures: (A) 900 K; (B) 1200 K; and (C) 1500 K.
We further evaluated the mechanical properties of the CuB monolayer by computing its elastic constants. Its elastic constants, i.e. C11 = C22 = 138.65 N/m, C12 = 45.35 N/m, and C66 = 55.49 N/m, well satisfy the mechanical stability criteria for an orthorhombic 2D sheet (C11C22 > C122, C66 > 0). The in-plane Young’s moduli along a and b directions can be computed by Ya = Yb = (C11C22 - C122)/C22 = 123.81 N/m, smaller than that of graphene (332 N/m)[84] and close to that of MoS2 monolayer (128 N/m)[85], which suggests that the CuB monolayer has strong mechanical stability and is promising for mechanical applications. Additionally, the Poisson’s ratio of the CuB monolayer can be calculated as va = vb = C12/C11 = 0.33 in both a and b directions; these values are larger than the corresponding ones for graphene (0.17)[86] and h-BN (0.23)[87] and are comparable with the Poisson’s ratio for MoS2 (0.29)[88].
Moreover, a comprehensive global minimum search was carried out for CuB by employing the PSO method. The computations give two low-lying configurations of 2D CuB, which are labeled CuB-I and CuB-II, respectively [Figure 6A and B]. Actually, CuB-I is the ppB-containing CuB monolayer, as discussed above. The structure of CuB-II (Pmmn, No. 59) can be described as an alternating zigzag chain of Cu atoms and a linear chain of B atoms, which is dynamically stable without any appreciable imaginary frequency [Figure 6C]. Our DFT computations showed that CuB-I is 94 meV per atom lower in energy than CuB-II; thus, our designed CuB monolayer (CuB-I) is indeed the global minimum structure in the 2D space.
Electronic properties of the CuB monolayer
We also investigated the band structure of the CuB monolayer by HSE functional, and essentially the same results as those by Jia et al.[49] were obtained; thus, detailed discussions are not given here. Briefly, there are three band lines across the Fermi level, and therefore CuB monolayer is metallic.
The projected density-of-states (PDOS) show that both B-p states and Cu-d states are dominant at the peaks of DOS around the Fermi level, indicating the highly hybrid B and Cu orbitals nearby the Fermi level, which further supports the strong band interactions between Cu and B atoms in the CuB framework [Figure 7]. The high density of electron states around the Fermi level suggests that sufficient electrons are available to participate in the electronic transport, thus contributing to the outstanding electric conductivity of the CuB monolayer. The concomitant electric conductivity is consistent with the well-delocalized electrons, as revealed by our ELF and DCD analyses in this study.
Superconductivity of the CuB monolayer
Inspired by the recently discovered superconductor MgB2 with a high Tc of 39 K[89], we theoretically calculated the electron−phonon coupling (EPC) and investigated the potential superconductivity of 2D CuB nanosheets. The component Cu is a heavy element, while B is a light element. Although CuB and MgB2 have completely different geometric structures, they do share some similar properties: the metallic nature with substantial electronic states at the Fermi level and the existence of strong covalent bonding[90]. Thus, we expected that the CuB monolayer might be superconducting.
Using the Quantum Expresso (QE) code, we first calculated the phonon dispersion of the CuB monolayer. The QE-calculated phonon dispersion from QE is consistent with the VASP result discussed above, which confirms the reliability of our approach.
Based on the phonon dispersions obtained by QE, we calculated the electron−phonon coupling (ECP) and further investigated the potential superconductivity of the CuB monolayer. The superconducting temperature (Tc) was estimated by the Allan−Dynes-modified McMillan’s approximation[91] of the Eliashberg equation:
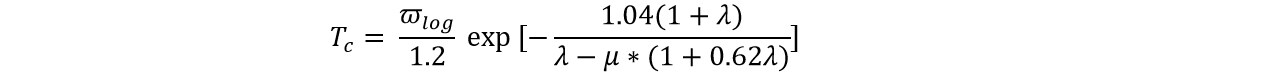
where μ* is the Coulomb pseudopotential, λ is the overall electron−phonon coupling strength computed from the frequency-dependent Eliashberg spectral function α2F(ω), and ωlog is the logarithmic average phonon frequency. Note that this method has been widely used to predict superconductive 2D monolayers[44,92-94].
Since no exact method is available to determine the parameter μ* yet, here we estimated the μ* value by comparing the calculated Tc with the experimentally known MgB2 results. If μ* is set as 0.05, the Tc of 36.9 K for MgB2 with a λ of 0.71 is obtained, which is in good agreement with the experimental Tc value (40 K) and λ value (~ 0.75)[95]. Thus, μ* = 0.05 was used to estimate Tc for the 2D CuB monolayer.
Using the above-determined μ* value (0.05), the EPC parameter λ was calculated to be 0.51, suggesting a strong EPC effect; notably, the estimated superconducting critical temperature Tc is as high as 4.6 K, which is higher than those of the previously reported Y2C (0.9 K)[96] and Co2C (3.4 K)[97] monolayers and is comparable to that of the AlB6 (4.7 K) nanosheet[98].
Previous literature demonstrates that tensile strain may greatly influence the superconducting property[99]. Thus, we examined the strain effect for the CuB monolayer. Our computations showed that the CuB nanosheet is stable under strains of 0% ≤ ɛ ≤ 10%. Remarkably, the predicted superconducting Tc reaches its highest temperature of 21 K when a tensile strain of 10% is adopted. These results suggest that the CuB nanosheets could be potentially utilized in future superconducting applications.
CONCLUSION
Inspired by the bonding pattern of the B2Cu6H6 molecule, we predicted the ppB-containing 2D CuB sheet by DFT computations, ab inito molecular dynamics simulations, and a comprehensive crystal structure search. The global minimum CuB monolayer is thermodynamically, dynamically, mechanically, and thermally stable. The electron donation and back donation between Cu and B atoms contribute to stabilizing ppB in the CuB monolayer. Young’s modulus analysis showed that the CuB monolayer has promising mechanical properties. This CuB monolayer material is metallic and predicted to be phonon-mediated superconducting with an estimated critical temperature (Tc) of 4.6 K. With the advancement of experimental techniques in fabricating 2D materials, we strongly believe that the CuB monolayer could be synthesized experimentally on some suitable substrate. Together with the progress recently achieved[49-51], this work could open a new branch of 2D copper boride layers with exceptional structures and fascinating properties.
DECLARATIONS
Authors’ contributionsConceptualization, investigation, writing - original draft: Tu K
Conceptualization, supervision, resources, writing - review & editing: Chen Z
Investigation, data analysis and interpretation: Gu J, Lu L, Yuan S, Zhou L
Availability of data and materialsNot applicable.
Financial support and sponsorshipThis work was supported by the NSF Centre for the Advancement of Wearable Technologies (Grant 1849243) and by NASA (Grant Number 80NSSC19M0236). A portion of the calculations used the resources of the Compute and Data Environment for Science (CADES) at ORNL and of the National Energy Research Scientific Computing Centre, which are supported by the Office of Science of the U.S. DOE under Contract No. DE-AC05-00OR22750 and DE-AC02-05CH11231, respectively. Some of the work was performed at the Center for Nanophase Materials Sciences, a U.S. DOE Office of Science User Facility.
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2022.
REFERENCES
1. Balakrishnarajan MM, Hoffmann R. Electron-deficient bonding in rhomboid rings. J Am Chem Soc 2004;126:13119-31.
2. Tang H, Ismail-Beigi S. Novel precursors for boron nanotubes: the competition of two-center and three-center bonding in boron sheets. Phys Rev Lett 2007;99:115501.
3. Yang X, Ding Y, Ni J. Ab initio prediction of stable boron sheets and boron nanotubes: structure, stability, and electronic properties. Phys Rev B 2008:77.
4. Penev ES, Bhowmick S, Sadrzadeh A, Yakobson BI. Polymorphism of two-dimensional boron. Nano Lett 2012;12:2441-5.
5. Wu X, Dai J, Zhao Y, Zhuo Z, Yang J, Zeng XC. Two-dimensional boron monolayer sheets. ACS Nano 2012;6:7443-53.
7. Sergeeva AP, Popov IA, Piazza ZA, et al. Understanding boron through size-selected clusters: structure, chemical bonding, and fluxionality. Acc Chem Res 2014;47:1349-58.
8. Zhang Z, Penev ES, Yakobson BI. Two-dimensional boron: structures, properties and applications. Chem Soc Rev 2017;46:6746-63.
9. Szwacki N, Sadrzadeh A, Yakobson BI. B80 fullerene: an Ab initio prediction of geometry, stability, and electronic structure. Phys Rev Lett 2007;98:166804.
10. Liu Y, Penev ES, Yakobson BI. Probing the synthesis of two-dimensional boron by first-principles computations. Angew Chem Int Ed Engl 2013;52:3156-9.
11. Zhang H, Xie Y, Zhang Z, et al. Dirac nodal lines and tilted semi-dirac cones coexisting in a striped boron sheet. J Phys Chem Lett 2017;8:1707-13.
12. Singh AK, Sadrzadeh A, Yakobson BI. Probing properties of boron alpha-tubes by Ab Initio calculations. Nano Lett 2008;8:1314-7.
13. Zhao J, Wang L, Li F, Chen Z. B(80) and other medium-sized boron clusters: core-shell structures, not hollow cages. J Phys Chem A 2010;114:9969-72.
14. Li F, Jin P, Jiang DE, et al. B80 and B101-103 clusters: remarkable stability of the core-shell structures established by validated density functionals. J Chem Phys 2012;136:074302.
15. Piazza ZA, Hu HS, Li WL, Zhao YF, Li J, Wang LS. Planar hexagonal B(36) as a potential basis for extended single-atom layer boron sheets. Nat Commun 2014;5:3113.
16. Mannix AJ, Zhou XF, Kiraly B, et al. Synthesis of borophenes: anisotropic, two-dimensional boron polymorphs. Science 2015;350:1513-6.
17. Feng B, Zhang J, Zhong Q, et al. Experimental realization of two-dimensional boron sheets. Nat Chem 2016;8:563-8.
19. Wu R, Drozdov IK, Eltinge S, et al. Large-area single-crystal sheets of borophene on Cu(111) surfaces. Nat Nanotechnol 2019;14:44-9.
21. Xie Z, Meng X, Li X, et al. Two-dimensional borophene: properties, fabrication, and promising applications. Research (Wash D C) 2020;2020:2624617.
22. Kaneti YV, Benu DP, Xu X, Yuliarto B, Yamauchi Y, Golberg D. Borophene: two-dimensional boron monolayer: synthesis, properties, and potential applications. Chem Rev 2022;122:1000-51.
23. Ou M, Wang X, Yu L, et al. The emergence and evolution of borophene. Adv Sci (Weinh) 2021;8:2001801.
24. Zhang Z, Yang Y, Gao G, Yakobson BI. Two-dimensional boron monolayers mediated by metal substrates. Angew Chem 2015;127:13214-8.
25. Xu SG, Li XT, Zhao YJ, et al. Two-dimensional semiconducting boron monolayers. J Am Chem Soc 2017;139:17233-6.
26. Li W, Chen X, Jian T, Chen T, Li J, Wang L. From planar boron clusters to borophenes and metalloborophenes. Nat Rev Chem 2017:1.
27. Romanescu C, Galeev TR, Li W, Boldyrev AI, Wang L. Aromatic metal-centered monocyclic boron rings: Co©B8− and Ru©B9−. Angew Chem 2011;123:9506-9.
28. Popov IA, Jian T, Lopez GV, Boldyrev AI, Wang LS. Cobalt-centred boron molecular drums with the highest coordination number in the CoB16- cluster. Nat Commun 2015;6:8654.
29. Zhang H, Li Y, Hou J, Tu K, Chen Z. FeB6 monolayers: the Graphene-like material with hypercoordinate transition metal. J Am Chem Soc 2016;138:5644-51.
30. Zhang H, Li Y, Hou J, Du A, Chen Z. Dirac state in the FeB2 monolayer with graphene-like boron sheet. Nano Lett 2016;16:6124-9.
31. Hoff V, Henricus J. Sur les formules de structure dans l’espace. Archives néerlandaises des sciences exactes et naturelles 1874; 9:445-454.
32. Bel L, Achille J. Sur les relations qui existent entre les formules atomiques des corps organiques et le pouvoir rotatoire de leurs dissolutions. Bulletin de la Société Chimique de Paris 1874; 22:337-347.
33. Yang LM, Ganz E, Chen Z, Wang ZX, Schleyer Pv. Four decades of the chemistry of planar hypercoordinate compounds. Angew Chem Int Ed Engl 2015;54:9468-501.
34. Wang Y, Li Y, Chen Z. Planar hypercoordinate motifs in two-dimensional materials. Acc Chem Res 2020;53:887-95.
35. Yam VW, Fung WK, Cheung K. Luminescence behavior of polynuclear alkynylcopper(I) Phosphines. J Cluster Sci 1999; 10:37-69.
36. Vega A, Calvo V, Spodine E, Zárate A, Fuenzalida V, Saillard JY. A novel copper cobalt inorganometallic cluster. Synthesis, structure and bonding analysis of Cu(3)[mu(2)-(CCHCo(2)(CO)(6))](3). Inorg Chem 2002;41:3389-95.
37. Tsipis AC, Tsipis CA. Hydrometal analogues of aromatic hydrocarbons: a new class of cyclic hydrocoppers(I). J Am Chem Soc 2003;125:1136-7.
38. Boca R, Dlhán L, Mezei G, Ortiz-Pérez T, Raptis RG, Telser J. Triangular, ferromagnetically-coupled CuII 3-pyrazolato complexes as possible models of particulate methane monooxygenase (pMMO). Inorg Chem 2003;42:5801-3.
39. Gawande MB, Goswami A, Felpin FX, et al. Cu and Cu-based nanoparticles: synthesis and applications in catalysis. Chem Rev 2016;116:3722-811.
40. Bhanushali S, Ghosh P, Ganesh A, Cheng W. 1D copper nanostructures: progress, challenges and opportunities. Small 2015;11:1232-52.
41. Yang L, Frauenheim T, Ganz E. Properties of the free-standing two-dimensional copper monolayer. J Nanomater 2016;2016:1-6.
42. Yang LM, Bačić V, Popov IA, et al. Two-dimensional Cu2Si monolayer with planar hexacoordinate copper and silicon bonding. J Am Chem Soc 2015;137:2757-62.
43. Feng B, Fu B, Kasamatsu S, et al. Experimental realization of two-dimensional Dirac nodal line fermions in monolayer Cu2Si. Nat Commun 2017;8:1007.
44. Yan L, Liu P, Bo T, et al. Emergence of superconductivity in a Dirac nodal-line Cu2Si monolayer: ab initio calculations. J Mater Chem C 2019;7:10926-32.
45. Ma Y, Kou L, Dai Y, Heine T. Two-dimensional topological insulators in group-11 chalcogenide compounds: M2Te(M=Cu,Ag). Phys Rev B 2016:93.
46. Yang LM, Popov IA, Boldyrev AI, Heine T, Frauenheim T, Ganz E. Post-anti-van’t Hoff-Le Bel motif in atomically thin germanium-copper alloy film. Phys Chem Chem Phys 2015;17:17545-51.
47. Li S, Ren G, Miao C, Jin Z. M4H4X: Hydrometals (M = Cu, Ni) containing tetracoordinate planar nonmetals (X=B, C, N, O). Angew Chem 2004;116:1395-7.
48. Li S, Miao C, Ren G. D5h Cu5H5X: Pentagonal hydrocopper Cu5H5 containing pentacoordinate planar nonmetal centers (X = B, C, N, O). Eur J Inorg Chem 2004;2004:2232-4.
49. Jia J, Zhang H, Wang Z, Zhao J, Zhou Z. A Cu2B2 monolayer with planar hypercoordinate motifs: an efficient catalyst for CO electroreduction to ethanol. J Mater Chem A 2020;8:9607-15.
50. Weng X, He X, Hou J, et al. First-principles prediction of two-dimensional copper borides. Phys Rev Materials 2020:4.
52. Becke AD. Density-functional thermochemistry. III. The role of exact exchange. J Chem Phys 1993;98:5648-52.
53. Lee C, Yang W, Parr RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys Rev B Condens Matter 1988;37:785-9.
54. Stephens PJ, Devlin FJ, Chabalowski CF, Frisch MJ. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J Phys Chem 1994;98:11623-7.
57. Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B 1999;59:1758-75.
58. Kresse G, Hafner J. Ab initio molecular dynamics for liquid metals. Phys Rev B Condens Matter 1993;47:558-61.
59. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett 1996;77:3865-8.
60. Heyd J, Scuseria GE, Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J Chem Phys 2003;118:8207-15.
61. Becke AD, Edgecombe KE. A simple measure of electron localization in atomic and molecular systems. J Chem Phys 1990;92:5397-403.
62. Silvi B, Savin A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994;371:683-6.
63. Galeev TR, Dunnington BD, Schmidt JR, Boldyrev AI. Solid state adaptive natural density partitioning: a tool for deciphering multi-center bonding in periodic systems. Phys Chem Chem Phys 2013;15:5022-9.
64. Clark SJ, Segall MD, Pickard CJ, et al. First principles methods using CASTEP. Z Kristallogr - Cryst Mater 2005;220:567-70.
65. Segall MD, Shah R, Pickard CJ, Payne MC. Population analysis of plane-wave electronic structure calculations of bulk materials. Phys Rev B 1996; 54:16317-16320.
66. Togo A, Tanaka I. First principles phonon calculations in materials science. Scr Mater 2015;108:1-5.
67. Martyna GJ, Klein ML, Tuckerman M. Nosé-Hoover chains: the canonical ensemble via continuous dynamics. J Chem Phys 1992;97:2635-43.
68. Giannozzi P, Baroni S, Bonini N, et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J Phys Condens Matter 2009;21:395502.
69. Savrasov SY, Savrasov DY, Andersen OK. Linear-response calculations of electron-phonon interactions. Phys Rev Lett 1994;72:372-5.
70. Kurth S, Marques M, Lüders M, Gross EKU. Local density approximation for superconductors. Phys Rev Lett 1999;83:2628-31.
71. Moret ME, Zhang L, Peters JC. A polar copper-boron one-electron σ-bond. J Am Chem Soc 2013;135:3792-5.
72. Holler S, Tüchler M, Belaj F, Veiros LF, Kirchner K, Mösch-Zanetti NC. Thiopyridazine-based copper boratrane complexes demonstrating the Z-type nature of the ligand. Inorg Chem 2016;55:4980-91.
73. Wang Y, Quillian B, Wei P, et al. A stable, neutral diborene containing a B=B double bond. J Am Chem Soc 2007;129:12412-3.
74. Zhou M, Tsumori N, Li Z, Fan K, Andrews L, Xu Q. OCBBCO: a neutral molecule with some boron-boron triple bond character. J Am Chem Soc 2002;124:12936-7.
75. Braunschweig H, Dewhurst RD, Hammond K, Mies J, Radacki K, Vargas A. Ambient-temperature isolation of a compound with a boron-boron triple bond. Science 2012;336:1420-2.
76. Wiberg K. Application of the pople-santry-segal CNDO method to the cyclopropylcarbinyl and cyclobutyl cation and to bicyclobutane. Tetrahedron 1968;24:1083-96.
77. Harper LK, Shoaf AL, Bayse CA. Predicting trigger bonds in explosive materials through wiberg bond index analysis. Chem Phys Chem 2015; 16:3886-3892.
80. Reed AE, Weinhold F. Natural bond orbital analysis of near-Hartree-Fock water dimer. J Chem Phys 1983;78:4066-73.
83. Hirshfeld FL. Bonded-atom fragments for describing molecular charge densities. Theoret Chim Acta 1977;44:129-38.
84. Lee C, Wei X, Kysar JW, Hone J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008; 321:385-388.
85. Cai Y, Zhang G, Zhang YW. Polarity-reversed robust carrier mobility in monolayer MoS₂ nanoribbons. J Am Chem Soc 2014;136:6269-75.
86. Wei X, Fragneaud B, Marianetti CA, Kysar JW. Nonlinear elastic behavior of graphene: Ab initio calculations to continuum description. Phys Rev B 2009:80.
87. Peng Q, Ji W, De S. Mechanical properties of the hexagonal boron nitride monolayer: Ab initio study. Comput Materi Sci 2012;56:11-7.
88. Cooper RC, Lee C, Marianetti CA, Wei X, Hone J, Kysar JW. Nonlinear elastic behavior of two-dimensional molybdenum disulfide. Phys Rev B 2013:87.
89. Nagamatsu J, Nakagawa N, Muranaka T, Zenitani Y, Akimitsu J. Superconductivity at 39K in magnesium diboride. Nature 2001;410:63-4.
90. Kortus J, Mazin II, Belashchenko KD, Antropov VP, Boyer LL. Superconductivity of metallic boron in MgB2. Phys Rev Lett 2001;86:4656-9.
91. Allen PB, Dynes RC. Transition temperature of strong-coupled superconductors reanalyzed. Phys Rev B 1975;12:905-22.
93. Singh S, Romero AH, Mella JD, et al. High-temperature phonon-mediated superconductivity in monolayer Mg2B4C2. npj Quantum Mater 2022:7.
94. Zhang X, Zhou Y, Cui B, Zhao M, Liu F. Theoretical discovery of a superconducting two-dimensional metal-organic framework. Nano Lett 2017;17:6166-70.
95. Bud'ko SL, Lapertot G, Petrovic C, Cunningham CE, Anderson N, Canfield PC. Boron isotope effect in superconducting MgB2. Phys Rev Lett 2001;86:1877-80.
97. Wang L, Xu C, Liu Z, et al. Magnetotransport properties in high-quality ultrathin two-dimensional superconducting Mo2C crystals. ACS Nano 2016;10:4504-10.
98. Song B, Zhou Y, Yang HM, et al. Two-dimensional anti-van’t hoff/Le Bel array AlB6 with high stability, unique motif, triple dirac cones, and superconductivity. J Am Chem Soc 2019;141:3630-40.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Tu K, Gu J, Lu L, Yuan S, Zhou L, Chen Z. CuB monolayer: a novel 2D anti-van't Hoff/Le Bel nanostructure with planar hyper-coordinate boron/copper and superconductivity. J Mater Inf 2022;2:13. http://dx.doi.org/10.20517/jmi.2022.10
AMA Style
Tu K, Gu J, Lu L, Yuan S, Zhou L, Chen Z. CuB monolayer: a novel 2D anti-van't Hoff/Le Bel nanostructure with planar hyper-coordinate boron/copper and superconductivity. Journal of Materials Informatics. 2022; 2(3): 13. http://dx.doi.org/10.20517/jmi.2022.10
Chicago/Turabian Style
Tu, Kaixiong, Jinxing Gu, Linguo Lu, Shijun Yuan, Long Zhou, Zhongfang Chen. 2022. "CuB monolayer: a novel 2D anti-van't Hoff/Le Bel nanostructure with planar hyper-coordinate boron/copper and superconductivity" Journal of Materials Informatics. 2, no.3: 13. http://dx.doi.org/10.20517/jmi.2022.10
ACS Style
Tu, K.; Gu J.; Lu L.; Yuan S.; Zhou L.; Chen Z. CuB monolayer: a novel 2D anti-van't Hoff/Le Bel nanostructure with planar hyper-coordinate boron/copper and superconductivity. J. Mater. Inf. 2022, 2, 13. http://dx.doi.org/10.20517/jmi.2022.10
About This Article
Copyright
Data & Comments
Data
 Cite This Article 13 clicks
Cite This Article 13 clicks




















Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.