Giant rashba splitting of confined Te chains in nanotubes: the size-, chirality-, and type- effects of nanotubes
Abstract
Understanding the coupling between one-dimensional (1D) materials and their protective materials is essential for developing nanodevices. Herein, we investigate the effect of the size, chirality, and type of nanotubes [such as carbon/boron nitride nanotubes (CNTs/BNNTs)] on the atomic and electronic structures of confined Te chains using density functional theory. We find that the optimal configurations of the Te chains confined in CNTs/BNNTs depend strongly on the size of the nanotubes but weakly on their chirality and type. Furthermore, the Te@BNNTs exhibit giant Rashba splitting with a Rashba constant of up to 2.65 eV Å, while the Te@CNTs show no splitting. This is mainly due to the large bandgap of the BNNTs, as well as the enhanced symmetry breaking of the Te chains when confined. Our findings provide a basis for the design of nano spin devices through protective materials.
Keywords
INTRODUCTION
In recent years, tellurium has attracted the interest of researchers because of its excellent transport properties and ability to form large-area air-stable two-dimensional (2D) thin films[1-4]. 2D Te films are composed of Te chains with van der Waals (vdW) interactions between the chains[5-7], which are expected to separate Te chains, even to the limit of the single-chain scale[8-10]. Single Te chains are expected to exhibit interesting physical properties that largely differ from the bulk[11]. For example, helical Te chains have a bandgap of ~1.53 eV at room temperature[12], in contrast to the value of 0.35 eV for the bulk. The symmetry breaking of Te chains due to their unique chiral characteristics leads to strong spin-orbit interactions and Rashba splitting. An isolated single Te chain was predicted to have a large Rashba constant of up to 2.17 eV with 23.13% strain[12]. However, single Te chains are inaccessible experimentally because they can easily crimp and adsorb small molecules from the environment, thereby degrading their performance. Nanotubes, such as carbon/boron nitride nanotubes (CNTs/BNNTs), serve as excellent protective materials for these nano-chains, due to their unique 1D hollow structure and chemical stability[8-10,13-15]. For instance, Pham et al. successfully synthesized the quasi 1D transition metal trichalcogenide NbSe3 (niobium triselenide) in the few-chain limit confined in CNTs and BNNTs[9]. Medeiros et al. experimentally observed Te chains encapsulated inside CNTs with diameters between 0.7 and 1.1 nm[8]. Te chains couple with the confining nanotubes, which affects their atomic and electronic structures. Nevertheless, disentangling the complicated coupling remains a challenge.
Previous works have mainly focused on the influence of the size of the nanotubes on the confined Te chains. For example, the number of Te chains decreases from triple, double to even single, with decreasing the diameter of the nanotubes[16]. In small-sized nanotubes, these 1D atomic chains undergo a structural change[17,18] and phase transition. S and Se encapsulated in CNTs adopt linear, zigzag, or helical structures depending on the inner diameter of the CNTs[19,20]. The Peierls structural distortion occurs for single Te chains[8]. Apart from the above structural change, Qin et al. predicted that the bandgap of Te increases monotonically from 0.35 eV in bulk to 0.68 eV for three Te chains and eventually reaches 1.51 eV in the single-chain limit due to the quantum confinement effect[16]. Although some works have synthesized 1D chains confined in both CNTs and BNNTs, they provide no insight into their effects on the electronic structure of the confined chains[9,16,21]. Furthermore, whether or not the chirality of the nanotubes plays a role remains unclear.
Therefore, herein, we systematically explore the effect of nanotube size and chirality on the atomic and electronic structures of Te chains confined in CNTs/BNNTs by density functional theory. We find that the tube size predominates in determining the configurations of the confined Te chains. The Te@BNNTs show giant Rashba splitting with a Rashba constant of up to 2.65 eV Å, which is the highest among known pure 1D systems, while the Te@CNTs show no Rashba splitting. This is because the large bandgap of the BNNTs accommodates and maintains the band edges of the Te chains, while the CNTs with a zero bandgap cannot. Our findings provide a basis for the construction of nano spin devices and lay a foundation for the design of new nanoelectronic devices.
MATERIALS AND METHODS
DFT calculations
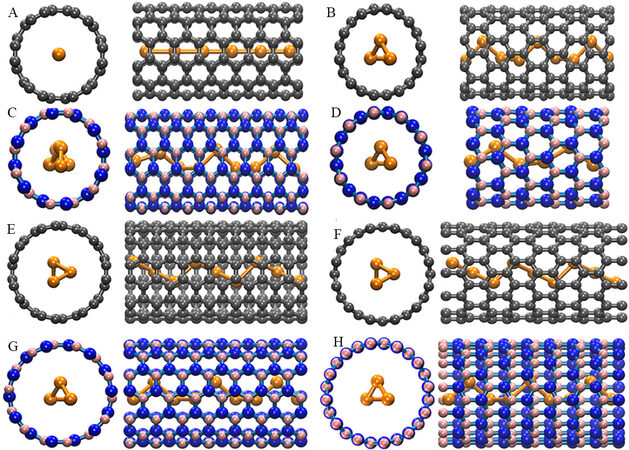
All calculations were performed using the CASTEP code with ultrasoft pseudopotentials[22]. We employed a sequence of Te@CNT and Te@BNNT structures that were periodic along the c-axis direction [Figure 1]. In the non-periodic directions, a vacuum of ~40 Å was adopted to avoid spurious interactions between the periodic images. Considering the different lattice constants between the Te chains and nanotubes, the combination between them was optimized by modulating the number of unit cells to reduce the strain. For example, one unit cell of Te chains matched with two unit cells of CNTs resulted in a 12.5% compressive stress to the confined Te chains relative to the free chains[12]. The geometric and energetic details were obtained with Perdew-Burke-Ernzerhof[23] augmented with the Tkatchenko-Scheffler[24] method (PBE+TS). A k-point separation of 0.02 Å-1 and an energy cutoff of 600 eV for the plane-wave basis set were adopted in all calculations. The spin-orbital coupling (SOC) effect was included for the calculations of the more accurate bandgap values. Overall, the geometric configurations were optimized until the maximum force in the chain of the directions was less than 0.01 eV/Å and the convergence of the total energy was less than 1 meV/atom.
Energy calculations
We adopt the adsorption energy (Ead) to characterize the stability of the Te@CNT and Te@BNNT systems:
Ead = (Etotal - Ent - ETe)/x (1)
where Etotal is the total energy of the Te@CNTs or Te@BNNTs, Ent is the energy of the CNTs or BNNTs, ETe is the energy of the single Te chains and x is the number of Te atoms.
RESULTS AND DISCUSSION
To systematically study how the size, chirality, and type of the nanotubes affect the atomic and electronic structures of the single Te chains confined in nanotubes, we consider two groups of CNTs/BNNTs with different sizes, namely, (6, 6)/(10, 0) and (7, 7)/(12, 0), each of which contains armchair and zigzag nanotubes, thereby helping us to study the size and chirality effects individually. The small-sized group [i.e., (6, 6) and (10, 0)] represented the smallest nanotubes that can accommodate a single Te chain, given that the vdW radii of C/B/N (RvdW, C/B/N) and Te (RvdW, Te) are 1.70, 1.68, 1.55 and 2.06 Å, respectively
Structural characterization
Due to the different lattice constants of the Te chains and nanotubes, their combination is inevitably accompanied by stretching or compression of the softer Te chains. To find the optimal mismatch, we consider a wide range of strains from -20% to 60%, given that the unique helical structure of the Te chains can bear a large strain without breaking. With increasing strain, we find that the helical Te chains in the range of small strains transform to zigzag chains and then to straight chains in the range of large strains, which is similar to the scenario of free chains under various stresses[12]. The global minima of the adsorption energy curve refer to the optimal configurations of Te chains confined in CNTs and BNNTs.
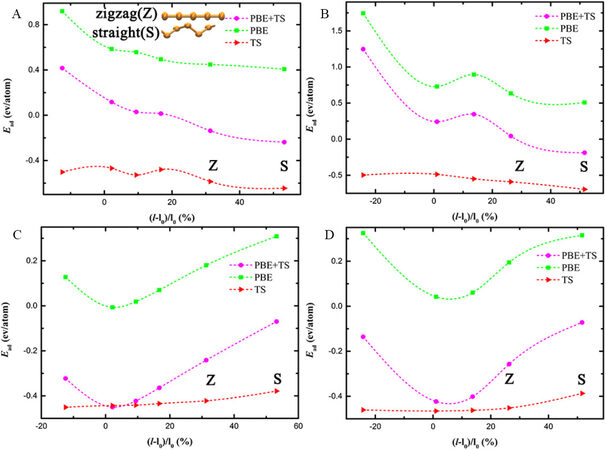
We first focus on the group of nanotubes with smaller sizes, i.e., the (6, 6) and (10, 0) CNTs. In Figure 2A, the adsorption energy between the Te chains and (6, 6) CNTs by PBE+TS decreases with strain, meaning that the straight Te chains are most likely the most stable configurations. For the Te@(10,0) CNTs in Figure 2B, the adsorption energy first decreases to a local minimum, then increases and finally decreases again. This non-monotonic trend suggests that both helical (with 1.1% strain) and linear Te chains can coexist in (10, 0) CNTs, unlike in (6, 6) CNTs. In the small-sized (6, 6) and (10, 0) CNTs, the Te chains undergo significant structural changes and a phase transition. We now consider the other group of nanotubes with larger sizes, i.e., the (7, 7) and (12, 0) CNTs. In Figure 2C and D, the adsorption energies for both the (7, 7) and (12, 0) CNTs follow a parabolic trend, reaching their global minima at strains very close to zero [2.14% for (7, 7) CNTs and 1.07% for (12, 0) CNTs]. The results indicate that the Te chains favor helical structures in the larger-sized CNTs. The helical chain structure under low strains exists in large nanotubes, while the straight structure is more favorable in small tubes. Therefore, the structure of the Te chains depends strongly on the nanotube size[29] but negligibly on the chirality. Chirality only plays a subtle role in the small-sized CNTs, i.e., two stable structures exist in the zigzag (10, 0) CNTs but only one occurs in the armchair (6, 6) CNTs.
Figure 2. Adsorption energy (Ead) of (A) Te@(6, 6) CNTs, (B) Te@(10, 0) CNTs, (C) Te@(7, 7) CNTs and (D) Te@(12, 0) CNTs. Z and S represent zigzag and straight chains, respectively, and the rest of the points default to helical chains.
Despite the similarity of their crystallographic structures, CNTs and BNNTs differ largely with regard to their electronic structures. For example, BNNTs have a large bandgap, while CNTs have no bandgap[28]. The large bandgap of BNNTs is expected to not interfere with the conduction band minimum (CBM) and valence band maximum (VBM) characteristics of the confined Te chains. Therefore, we next focus on the Te chains confined in the (6, 6), (10, 0), (7, 7) and (12, 0) BNNTs.
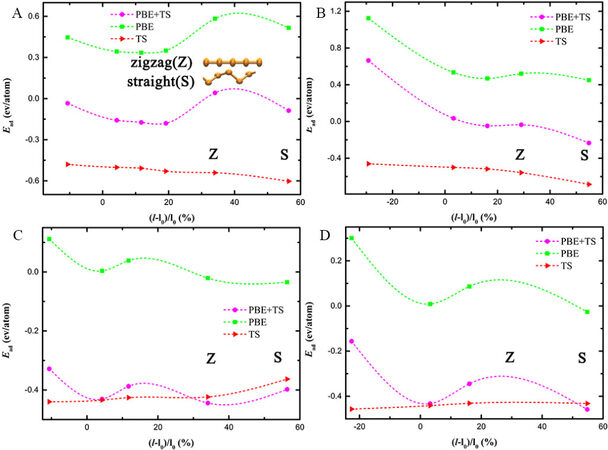
In Figure 3A, although the local minima reside far from the zero strain, the most stable configuration for the Te chains confined in the (6, 6) BNNTs is still the helical chain [the zigzag (Z) and straight (S) chains are marked in Figure 3, as opposed to the straight Te chains in the (6, 6) CNTs. In contrast, the helical and linear Te chains coexist in both the (10, 0) CNTs and BNNTs (see Figures 2B and 3B, respectively). For the Te@(7, 7) BNNTs and Te@(12, 0) BNNTs in Figure 3C and D, respectively, the local minima are close to the zero strain, indicating that the Te chains confined in these two BNNTs resemble the isolated free chain. The comparison between the Te@CNTs and Te@BNNTs reaches a consistent conclusion: the size of the nanotubes plays a dominating role in determining the confined configurations, while the chirality and type of the nanotubes play a secondary role.
Figure 3. Adsorption energy (Ead) of (A) Te@(6, 6) BNNTs, (B) Te@(10, 0) BNNTs, (C) Te@(7, 7) BNNTs and (D) Te@(12, 0) BNNTs. Z and S represent zigzag and straight chains, respectively, and the rest of the points default to helical chains.
In both Figures 2 and 3, the adsorption energy at the PBE level of theory exactly follows the trends of the overall adsorption energy, while the TS contribution to the total adsorption energy is insensitive to the strain, as indicated by the rather smooth curves. Therefore, the Pauli repulsion, well captured by the PBE method, determines the optimal structures of Te chains confined in the nanotubes, whereas the vdW interactions, well treated by the TS method, are only to bind Te chains and nanotubes together and stabilize them. This can be easily explained by the distance between the Te chains and nanotubes. In the small-sized tubes, the radius of the nanotubes is comparable to the sum of the vdW radius [D ≈ 2 (RvdW, C/B/N + RvdW, Te)]. The smaller distance between the Te chains and nanotubes in the helical and zigzag structures than in the straight state means that the short-ranged Pauli repulsion plays a significant role. This is why the contribution of PBE to the adsorption energy oscillates significantly with strain. In the large-sized nanotubes, the radius of the nanotubes is close to 3(RvdW, C/B/N + RvdW, Te), and thus the coupling is weaker than that in the small-sized group. The contribution of PBE decreases first because the helicity of the Te chains becomes smaller and the distance between the atoms on the Te chain and the nanotube becomes farther. The contribution of PBE increases due to the strain accumulated within the chains.
Band structure analysis
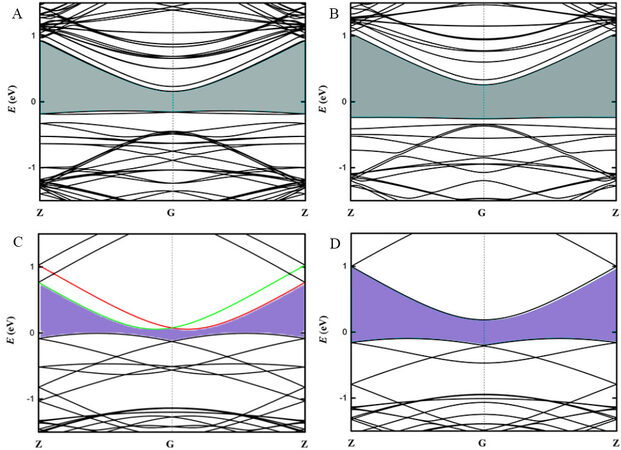
For the heavy Te element, the band structure calculations must account for the SOC effect. For the Te@CNTs systems, we tentatively computed the band structures of the straight Te chain, (6, 6) CNTs and Te@(6, 6) CNTs [Supplementary Figure 1]. Their comparison shows that although the CBM and VBM of the free Te chain significantly hybridize with those of the (6, 6) CNTs when combined, they are always trapped in the band structure of the (6, 6) CNTs, which should also hold for the (7, 7) and (12, 0) CNTs with similar zero bandgaps [Supplementary Figure 2]. To expose the CBM and VBM of the Te chain when combined, we turn to the only semiconducting (10, 0) CNTs. For the convenience of comparison, the (10, 0) BNNTs are employed (see other cases in Supplementary Figures 3 and 4).
Figure 4A and B show the band structure of the Te@(10, 0) CNTs (with a metastable helical Te chain at 1.1% strain) at the level of PBE+SOC/PBE theory. The bandgap greatly reduces by ~0.2 eV when including SOC (0.496 eV with PBE vs. 0.296 eV with PBE+SOC), which is consistent with the previous work[1]. The small bandgap for the (10, 0) CNTs (~0.9 eV) fails to accommodate and maintain the CBM and VBM of the Te chains. Figure 4C and D show the band structures of the Te@(10, 0) BNNTs (with a stable helical Te chain at 16.1% strain) at the level of PBE+SOC/PBE. Notably, we observe not only the reduced bandgaps (the values are 0.063/0.285 eV with/without SOC and ~5.5 eV for isolated BNNTs) but also the spin splitting in Figure 4C. A similar situation holds for other BNNTs: the bandgaps are 0.27 eV for the Te@(6, 6) BNNTs, 1.20 eV for the Te@(7, 7) BNNTs and 1.30 eV for the Te@(12, 0) BNNTs. Although the hybrid functionals (such as HSE) well describe the electronic structures of the nanotube systems[30], they are much more computationally demanding. Notably, in our previous study on the isolated Te chains[12], we employ both PBE+SOC and HSE+SOC functionals. HSE+SOC methods indeed lead to the more accurate bandgap and Rashba results but maintain the trend calculated with the PBE+SOC method. In this work, we are more focused on the trend, and thus the computationally efficient PBE functional is adopted.
Figure 4. Band structures of Te@(10, 0) CNTs with/without SOC (A)/(B) and Te@(10, 0) BNNTs with/without SOC (C)/(D). The Rashba splitting is highlighted, where the green and red lines are for the spin-up and spin-down bands, respectively.
The band splitting observed in the BNNTs after considering SOC is known as Rashba splitting. We employ the three most critical Rashba splitting parameters (ER, ΔkR and αR) to quantify the Rashba spin splitting strength. As shown in Supplementary Figure 5, the Rashba energy (ER) is the energy difference between the crossing point and the band edge. The Rashba momentum offset ΔkR is the moment splitting of the Rashba bands from the crossing point. The most widely discussed Rashba constant αR represents the strength of the Rashba effect, which can be derived from the equation αR = 2ER/ΔkR in low dimensional systems. Generally, large ER is beneficial to stabilizing the spin and large ΔkR indicates that a sufficient phase shift can be achieved for different spin channels. The resulting αR for the Te@BNNTs is 1.31 eV Å for the (6, 6) BNNTs (with a strain of 19.17%), 2.65 eV Å for the (10, 0) BNNTs (with a strain of 16.10%), 1.91 eV Å for the (7, 7) BNNTs (with a strain of 4.27%), and 1.76 eV Å for the (12, 0) BNNTs (with a strain of 3.2%). Among them, the Te@(10, 0) BNNTs show the largest Rashba constant and the other two parameters are listed in Table 1.
Rashba energy (ER), momentum offset (ΔkR) and Rashba parameter (αR)
| System | ER (meV) | kR (Å-1) | αR (eV Å) | Reference |
| Te@(6,6) BNNTs | 11.06 | 0.02 | 1.31 | This work |
| Te@(10,0) BNNTs | 20.64 | 0.02 | 2.65 | This work |
| Te@(7,7) BNNTs | 20.29 | 0.02 | 1.91 | This work |
| Te@(12,0) BNNTs | 20.60 | 0.02 | 1.76 | This work |
| Isolated Te chains | 24 | 0.057 | 0.84 | Ref[12] |
| Distorted-23.13% stretched Te | 111 | 0.102 | 2.18 | Ref[12] |
| InGaAs/InAlAs | < 1 | 0.028 | 0.51 | Ref[31] |
| Si-Au nanowire | N/A | 0.05 | N/A | Ref[32] |
| Pt/Si(111)nanowire | 81 | 0.12 | 1.36 | Ref[33] |
| Q2 Bi on In/Si(111) | 78.2 | 0.073 | 2.1 | Ref[34] |
The Te@CNTs do not have Rashba splitting, while Te@BNNTs do, indicating that the electronic structures of the internal Te chains depend on the type of nanotubes. Compared with the Te@CNTs, all the Te@BNNTs have large Rashba splitting, which is mainly due to the large bandgap of the BNNTs. For this reason, the CBM and VBM of the Te chains can reside in the large bandgap of the BNNTs and the Rashba splitting of the Te chains is maintained. The large bandgap of the BNNTs can, therefore, completely expose the band edge of the Te chains, while the zero band gap of the CNTs limits this performance. Apart from the intrinsic atomic SOC, the structural origin, i.e., the symmetry breaking, contributes to the large Rashba splitting. The bond length of the Te chains in the free state is 2.76 Å and the bond angle is 100.9°. When confined in nanotubes, the confinement induces a change in bond length and angle. For example, with the strain of 16.10%, the bond lengths of the Te chains in BNNTs are 2.74-2.75 Å and the bond angles are 116.1-116.3°. The comparison between free Te chains and confined Te demonstrates that confinement enhances the Rashba splitting through symmetry breaking.
Materials with large Rashba constants and energies provide us with more leeway in the choice of their spintronic properties. The free Te chains have already excelled over other 1D materials, such as 1D atomic Te chains and the distorted 23.13% stretched Te [Table 1][12]. Furthermore, the Rashba constant is 0.82 (0.99) eV Å for the Te chain in the (10, 5) CNTs (BNNTs) and 0.89 (0.94) eV Å for the Te chains without the CNTs (BNNTs) in previous work[12]. In addition, the ER of Te@BNNTs is ~20 meV, comparable to that of the single helical chain[12]. Compared to other systems, the αR of Te@(10, 0) BNNTs is up to 2.65 eV Å, which is three or four times larger than those of the other Rashba systems, such as Bi/Ag(111) surface alloys[35], InGaAs/InAlAs31 and Si(557)-Au nanowires[32]. The αR of the Te@(10, 0) BNNTs is comparable with that of some giant 1D Rashba systems, such as the αR in the Pt/Si(111) nanowire is 1.36 eV Å[33], the Q2 structure for Bi on In/Si(111) is 2.1 eV Å and the H1 structure for Bi on In/Si(111) is 3.1 eV Å[34]. Due to the existence of surface dangling bonds or the presence of the (semi) metallic surface states, the performance of these semiconductor nanowires degraded.
CONCLUSIONS
In this study, we have established how the size and chirality of CNTs/BNNTs affect the atomic and electronic structures of confined Te chains. The optimal structures of Te chains confined in CNTs and BNNTs are predominately determined by the size of the nanotubes rather than their chirality or type. Remarkably, the Te@BNNTs show even superior Rashba splitting, compared with the isolated Te chains, while the Te@CNTs show no splitting at all. The striking contrast is mainly due to the large bandgaps of BNNTs that accommodate and maintain the band edges of Te chains where the Rashba splitting emerges. Our results reveal an interesting conclusion: the relative independence of the electronic structure between the confined and protective materials is an essential prerequisite for protective realization without degrading the performance of confined materials. These results are expected to shed light on the development of nano spin devices.
DECLARATIONS
Authors’ contributionsMade substantial contributions to the conception and design of the study and performed data analysis and interpretation: Han J, Ma C, Gao W
Provided administrative, technical, and material support: Qi L, Gao W
Availability of data and materialsSupplementary materials are available from the Journal of Materials Informatics or the authors.
Financial support and sponsorshipThis work is supported by the National Natural Science Foundation of China (Nos. 21673095, 11974128, 51631004, 11774084, and 91833302), the Opening Project of the State Key Laboratory of High Performance Ceramics and Superfine Microstructure (SKL201910SIC), the Program for JLU (Jilin University) Science and Technology Innovative Research Team (Number 2017TD-09), and the computing resources of High Performance Computing Center of Jilin University.
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2022.
Supplementary MaterialsREFERENCES
1. Qi L, Han J, Gao W, Jiang Q. Monolayer tellurenyne assembled with helical telluryne: structure and transport properties. Nanoscale 2019;11:4053-60.
2. Wang Y, Qiu G, Wang R, et al. Field-effect transistors made from solution-grown two-dimensional tellurene. Nat Electron 2018;1:228-36.
3. Qiu G, Wang Y, Nie Y, et al. Quantum transport and band structure evolution under high magnetic field in few-layer tellurene. Nano Lett 2018;18:5760-7.
4. Zhu Z, Cai X, Yi S, et al. Multivalency-driven formation of Te-based monolayer materials: a combined first-principles and experimental study. Phys Rev Lett 2017;119:106101.
5. Doi T, Nakao K, Kamimura H. The valence band structure of tellurium. I. The k·p Perturbation Method. J Phys Soc Jpn 1970;28:36-43.
6. Martin RM, Lucovsky G, Helliwell K. Intermolecular bonding and lattice dynamics of Se and Te. Phys Rev B 1976;13:1383-95.
7. Du Y, Qiu G, Wang Y, et al. One-dimensional van der waals material tellurium: raman spectroscopy under strain and magneto-transport. Nano Lett 2017;17:3965-73.
8. Medeiros PVC, Marks S, Wynn JM, et al. Single-atom scale structural selectivity in Te nanowires encapsulated inside ultranarrow, single-walled carbon nanotubes. ACS Nano 2017;11:6178-85.
9. Pham T, Oh S, Stetz P, et al. Torsional instability in the single-chain limit of a transition metal trichalcogenide. Science 2018;361:263-6.
10. Kobayashi K, Yasuda H. Structural transition of tellurium encapsulated in confined one-dimensional nanospaces depending on the diameter. Chemical Physics Letters 2015;634:60-5.
11. Agapito LA, Kioussis N, Goddard WA 3rd, Ong NP. Novel family of chiral-based topological insulators: elemental tellurium under strain. Phys Rev Lett 2013;110:176401.
12. Han J, Zhang A, Chen M, Gao W, Jiang Q. Giant Rashba splitting in one-dimensional atomic tellurium chains. Nanoscale 2020;12:10277-83.
13. Walker KE, Rance GA, Pekker Á, et al. Growth of carbon nanotubes inside boron nitride nanotubes by coalescence of fullerenes: toward the world’s smallest coaxial cable. Small Methods 2017;1:1700184.
14. Nieto-Ortega B, Villalva J, Vera-Hidalgo M, Ruiz-González L, Burzurí E, Pérez EM. Band-gap opening in metallic single-walled carbon nanotubes by encapsulation of an organic salt. Angew Chem Int Ed Engl 2017;56:12240-4.
15. Komsa HP, Senga R, Suenaga K, Krasheninnikov AV. Structural distortions and charge density waves in iodine chains encapsulated inside carbon nanotubes. Nano Lett 2017;17:3694-700.
16. Qin J, Liao P, Si M, et al. Raman response and transport properties of tellurium atomic chains encapsulated in nanotubes. Nat Electron 2020;3:141-7.
17. Ilie A, Bendall JS, Nagaoka K, Egger S, Nakayama T, Crampin S. Encapsulated inorganic nanostructures: a route to sizable modulated, noncovalent, on-tube potentials in carbon nanotubes. ACS Nano 2011;5:2559-69.
18. Slade CA, Sanchez AM, Sloan J. Unprecedented new crystalline forms of SnSe in narrow to medium diameter carbon nanotubes. Nano Lett 2019;19:2979-84.
19. Fujimori T, dos Santos RB, Hayashi T, Endo M, Kaneko K, Tománek D. Formation and properties of selenium double-helices inside double-wall carbon nanotubes: experiment and theory. ACS Nano 2013;7:5607-13.
20. Fujimori T, Morelos-Gómez A, Zhu Z, et al. Conducting linear chains of sulphur inside carbon nanotubes. Nat Commun 2013;4:2162.
21. Liu M, Hisama K, Zheng Y, et al. Photoluminescence from SINGLE-WALLEd MoS2 nanotubes coaxially grown on boron nitride nanotubes. ACS Nano 2021;15:8418-26.
22. Segall MD, Lindan PJD, Probert MJ, et al. First-principles simulation: ideas, illustrations and the CASTEP code. J Phys : Condens Matter 2002;14:2717-44.
23. Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett 1996;77:3865-8.
24. Tkatchenko A, Scheffler M. Accurate molecular van der Waals interactions from ground-state electron density and free-atom reference data. Phys Rev Lett 2009;102:073005.
26. Hu S, Zhou Z, Robertson BE. Consistent approaches to van der Waals radii for the metallic elements. Zeitschrift für Kristallographie 2009;224:375-83.
27. Lanzillo NA, Kharche N, Nayak SK. Substrate-induced band gap renormalization in semiconducting carbon nanotubes. Sci Rep 2014;4:3609.
28. Xiang H, Yang J, Hou J, Zhu Q. First-principles study of small-radius single-walled BN nanotubes. Phys Rev B 2003:68.
29. Eliseev AA, Yashina LV, Kharlamova MV, Kiselev NA. Electronic properties of carbon nanotubes. In: M. Marulanda editor. Chapter 8: One-dimensional crystals inside single-walled carbon nanotubes: growth, structure and electronic properties. IntechOpen publisher; 2011. pp. 127-156
30. Pari S, Cuéllar A, Wong BM. Structural and electronic properties of graphdiyne carbon nanotubes from large-scale DFT calculations. J Phys Chem C 2016;120:18871-7.
31. Nitta J, Akazaki T, Takayanagi H, Enoki T. Gate control of spin-orbit interaction in an inverted I n0.53 G a0.47 As/I n0.52 A l0.48 as heterostructure. Phys Rev Lett 1997;78:1335-8.
32. Barke I, Zheng F, Rügheimer TK, Himpsel FJ. Experimental evidence for spin-split bands in a one-dimensional chain structure. Phys Rev Lett 2006;97:226405.
33. Park J, Jung SW, Jung MC, Yamane H, Kosugi N, Yeom HW. Self-assembled nanowires with giant Rashba split bands. Phys Rev Lett 2013;110:036801.
34. Tanaka T, Gohda Y. First-principles prediction of one-dimensional giant Rashba splittings in Bi-adsorbed In atomic chains. Phys Rev B 2018:98.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Han J, Qi L, Ma C, Gao W. Giant rashba splitting of confined Te chains in nanotubes: the size-, chirality-, and type- effects of nanotubes. J Mater Inf 2022;2:6. http://dx.doi.org/10.20517/jmi.2022.08
AMA Style
Han J, Qi L, Ma C, Gao W. Giant rashba splitting of confined Te chains in nanotubes: the size-, chirality-, and type- effects of nanotubes. Journal of Materials Informatics. 2022; 2(2): 6. http://dx.doi.org/10.20517/jmi.2022.08
Chicago/Turabian Style
Han, Jie, Liujian Qi, Cong Ma, Wang Gao. 2022. "Giant rashba splitting of confined Te chains in nanotubes: the size-, chirality-, and type- effects of nanotubes" Journal of Materials Informatics. 2, no.2: 6. http://dx.doi.org/10.20517/jmi.2022.08
ACS Style
Han, J.; Qi L.; Ma C.; Gao W. Giant rashba splitting of confined Te chains in nanotubes: the size-, chirality-, and type- effects of nanotubes. J. Mater. Inf. 2022, 2, 6. http://dx.doi.org/10.20517/jmi.2022.08
About This Article
Copyright
Data & Comments
Data

 Cite This Article 11 clicks
Cite This Article 11 clicks












Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.