Development of robust surfaces for harsh service environments from the perspective of phase formation and transformation
Abstract
The rise of the materials genome and materials informatics has enabled the accelerated development of robust surfaces for harsh service environments in the nuclear, aerospace and marine industries. Accurate information on the phase formation and transformation of materials (particularly coating materials) in synthesis and service processes is a prerequisite for the successful optimization of their properties. However, both these processes proceed under non-equilibrium conditions, making the traditional CALPHAD (CALculation of PHAse Diagrams) approach incapable of describing the phase relation and stability. Hence, this study provides a brief review on the recent research advances pertaining to the phase formation during coating deposition, the phase transformation in service and the materials optimization targeted for demanding working conditions. We also summarize the challenges of expanding phase diagram databases with a wide adaptability to metastable phase formation and non-equilibrium phase transformation in multicomponent systems. Through the elaboration of each research case, this review provides new insights into the surface protection of materials serving in harsh environments.
Keywords
Introduction
Stable operation and high reliability are among the critical requirements for the machinery used in the nuclear, aerospace and marine industries, where demanding working conditions encompassing high temperatures and pressures, corrosion, oxidation, irradiation and wear are typically encountered[1-3]. A lethal threat posed to the durability of machinery comes from the degradation of materials serving in harsh environments[4]. Thus, the ever-increasing demands for high-performance machinery heavily depend on the successful development of novel materials in synergy with appropriate surface engineering methods[5].
Conventionally, materials development depends mainly on the trial-and-error method, which is notorious for high resource consumption with low efficiency[6]. In addition, the growing trend of materials development, including coatings, towards multicomponent systems with complex structures, such as high entropy alloys[7], gradient nanostructures[8] and multilayered coatings[9], has rendered the conventional method incapable of sifting through candidate materials. In this context, the way in which materials are engineered has been essentially reformed with the rise of computer technology. Enlightened by the successful implementation of informatics in diverse fields such as biology, astronomy and social sciences, materials informatics, based on data exploration with the aid of computer simulations, allows one to extract knowledge and insight from massive data, provided, of course, that reliable databases exist[10,11]. However, the discrete nature of the available databases and the unestablished paradigm of processing-structure-properties result in the underutilization of informatics in materials design[12]. Thus far, a strong impetus in materials informatics has stemmed from the launches of integrated computational materials engineering (ICME)[13-15] and the Materials Genome Initiative (MGI)[15,16] in the last decade. As representative novel materials innovation methodologies, both ICME and the MGI produce large amounts of data through both high-throughput experiments and calculations[17].
High-throughput experiments, in general, encompass the highly efficient preparation, characterization and property evaluation of various categories of materials[18-20]. Prominent examples include the multi-target co-sputtering method to synthesize gradient multicomponent coatings[21], the diffusion multivariate method to prepare gradient multicomponent alloys[22] and the combinatorial material characterization approach using an integrated micro-beam X-ray fluorescence and diffraction system to determine the chemical composition and phase constitution of materials simultaneously[23]. Alternatively, high-throughput calculations incorporate simulation methods at different scales, from the atomistic level (e.g., first-principles calculations[24]), to the microscopic level (e.g., the calculation of phase diagrams[25] and diffusion simulations[26]), the mesoscopic level (e.g., the phase-field method[27]) and the macroscopic level (e.g., finite element analysis[28]). High-throughput experiments and calculations are not mutually exclusive; for example, high-throughput experiments can provide important input data to initiate simulations while high-throughput calculations can narrow the scope of materials to be tested. Furthermore, both of these methods can generate large quantities of data that can be included in materials databases[29].
All materials databases fall in two major categories, namely, a category related to the performance of materials and another category concerning the intrinsic characteristics of materials. In particular, phase diagram databases that describe the inherent thermodynamic, thermophysical and thermoelectric properties of materials represent an early example and illustrate the usefulness of reliable databases in materials design. Utilizing the reasonably predicted physical parameters based on density functional theory, the CALculation of PHAse Diagrams (CALPHAD) approach aided with first-principles calculations has become a prevalent choice in the establishment of phase diagram databases, as it avoids the inherent difficulties associated with experimental measurements of critical physical parameters[30]. Through the integration of the available data with appropriate calculation models, the calculated phase diagrams can map the relationships between crystal structure, temperature, composition and pressure for multicomponent systems with sufficient precision[31]. In practice, the quantitative design of new materials based on phase diagrams has proven to be effective in the development of bulk materials[32]. However, this methodology cannot be easily applied directly to coating deposition and service processes as both of them proceed under non-equilibrium conditions[33,34]. Thus, the desire to elongate the durability of materials (and coatings) serving in harsh environments necessitates the development of appropriate calculation models to describe these non-equilibrium processes[35].
Towards this end, this review introduces some of the recent research advances related to phase formation during coating deposition (Section 2), phase transformation in service (Section 3) and materials optimization (Section 4) targeted for demanding working conditions (as shown in Figure 1[36-38]). Through the elaboration of each research case, this review provides new insights into the surface protection of materials serving in harsh environments based on phase diagram databases.
Development of metastable phase formation diagrams for coating deposition processes
An in-depth understanding of the phase formation mechanism in coating deposition is a pre-condition for the accomplishment of novel coating designs. During the course of physical vapor deposition (PVD), for example, the material system is in a non-equilibrium state and metastable phases generally form. As such, the CALPHAD method that depends on phase equilibrium calculations is no longer suitable to directly construct the metastable phase formation diagram. It is therefore of significance to develop a new calculation model that combines thermodynamics with kinetics to quantitatively predict the metastable phase formation during coating deposition.
Phase formation mechanism
In a typical PVD process, gaseous atoms (or atomic clusters) rapidly cool from ultra-high temperatures and solid phases form almost simultaneously on the substrate surface[39]. The phase formation is thus controlled by the surface diffusion within a few layers of atoms deposited rather than the bulk diffusion across the entire coating[39]. A quantitative description of surface diffusional behavior starts with the atomic surface diffusion distance equation proposed by Einstein[40]:

where X is the diffusion distance, Ds is the surface diffusivity and t is the diffusion time. Based on Eq. (1), Cantor and Cahn[41] demonstrated that the diffusion time of a surface atom can be estimated using a/rD:

where v is the vibrational frequency of surface atoms, a is the individual jump distance, rD is the deposition rate, Qs is the activation energy for surface diffusion, k is the Boltzmann constant and T is the substrate temperature during deposition.
Equation (2) can be used to qualitatively describe the metastable phase formation in a coating system. For example, the diffusion distance of metal atoms (Cu, Ni and Fe) in face-centered cubic (fcc) Al has been evaluated based on Eq. (2) and the results show that the surface diffusion is insufficient at low temperatures and metastable phases are prone to form in the coating[41]. This is consistent with the experimental observation that Cu, Ni and Fe exist in the metastable fcc phase structure with a certain solubility, especially when the Al content is high, in contrast to the equilibrium phase diagrams that show negligible solubilities of Cu, Ni and Fe in the fcc-Al phase. It is also noted from Eq. (2) that Qs in the exponential function is the most pivotal parameter that affects the diffusion distance.
Taking this into account, Saksena et al.[42] studied phase formation in the Pt-Ir binary coating system with reference to the Pt-Au binary system. As shown in Figure 2A and B, the equilibrium phase diagrams of Pt-Ir and Pt-Au systems are reasonably similar, where the fcc-(
Figure 2. First-principles and CALPHAD calculated results for Pt-Ir and Pt-Au systems: (A) Pt-Ir equilibrium phase diagram; (B) Pt-Au equilibrium phase diagram; (C) formation enthalpies of fcc-(Pt, Ir) and fcc-(Pt, Au) phases; and (D) surface diffusion activation energy for an atom on Pt-Ir (111) and Pt-Au (111) surfaces. Figure reproduced from Ref.[42] with permission from Springer Nature.
Quantitative calculation model
With a qualitative relationship established between diffusion-related parameters and metastable phase formation, Chang et al.[43] selected the Cu-W binary coating as a model system and sought to achieve a quantitative description of the metastable phase formation in a PVD process. As shown in the equilibrium phase diagram of Figure 3A, the solubility between Cu and W is close to zero, whereas in the deposited coating, Cu and W reveal large mutual solubilities. On the basis of Eq. (2), Chang et al.[43] put forward the concept of the critical surface diffusion distance defined by the following equations:
Figure 3. Theoretical and experimental results for the Cu-W system: (A) calculated equilibrium phase diagram; (B) ln(rD) vs. 1000/Tc plot with phase boundary data from the experimental metastable phase formation diagram; (C) 3D atom-probe tomography data of Cu0.57W0.43 coating with the reconstructed needle and proxigram analysis of the composition; and (D) first-principles calculated diffusion activation barriers compared with experimental values. Figure reproduced from Refs.[43,44] with permissions from Elsevier and Taylor & Francis.

where Xc is the critical surface diffusion distance, Tc is the critical temperature at which the second phase forms at a specific constant deposition rate (rDn), z is the metastable solubility and Xc(1/2) is the critical diffusion distance at the half metastable solubility, i.e., at z = (zmax + zmin)/2.
According to Eq. (3), when the substrate temperature is lower than the critical temperature, the surface diffusion distance is lower than the critical value and a single metastable phase is most likely to form. In contrast, when the substrate temperature is higher than the critical value, the diffusion distance surpasses the critical distance and the propensity of second phase formation increases. The variation of critical temperature along with the change of deposition rate can be derived from the experimentally determined metastable Cu-W phase diagram, as shown in Figure 3B. The surface diffusion activation energy is therefore calculated and the results are well supported by both experiments and first-principles calculations [Figure 3C and D].
One should note that Eq. (4) needs to be used in conjunction with Eq. (3) when establishing a metastable phase formation diagram. Initially, the critical diffusion distance, Xc(1/2), at the half metastable solubility, z = (zmax + zmin)/2 is determined, with the other parameters in these two equations obtained from the CALPHAD approach, first-principles calculations and high-throughput deposition experiments. Afterwards, the relationship between temperature (or deposition rate) and metastable solubility is established and the metastable phase formation diagram can be plotted accordingly. As such, a new methodology to build non-equilibrium metastable phase formation diagrams based on the quantitative calculation model has been developed, with additional details regarding the implementation procedures available in Ref.[44]. The core of this methodology is the employment of the CALPHAD approach aided by first-principles calculations to simulate the surface diffusion of metastable phases. Utilizing only one set of high-throughput coating deposition experiment data as input values, the metastable phase formation diagrams of the coating system at different deposition rates can be calculated. The successful implementation of this methodology for the Cu-V binary system is shown in Figure 4, where the calculation results fit well with the experimental data[44].
Figure 4. Metastable Cu-V phase formation diagrams: (A) calculated and predicted diagrams using experimental data at 240 °C and a power density of 0.91 W·cm-2; validation using experimental data at power densities of (B) 0.91, (C) 3.64 and (D) 7.28 W·cm-2. Figure reproduced from Ref.[44] with permission from Taylor & Francis.
Model applicability
Cubic transition metal aluminum nitrides (TM-Al-N) represent a category of ternary coating systems commonly employed for surface protection in the materials processing, nuclear and aerospace industries[45-47]. In a TM-Al-N system, the solubility of Al in the fcc solid solution phase is a crucial factor that impacts the anti-wear and anti-corrosion properties of coatings[48]. However, rather than being constant, the solubility of Al changes in response to temperature variations, with the metastable phase formation diagram of the TM-Al-N system having therefore been determined merely by experiments[49].
Recently, by applying a newly-developed calculation model, Liu et al.[36,50] successfully predicted the metastable phase formation diagrams of the Ti-Al-N and V-Al-N coating systems. Using the V-Al-N system as an example, it can be seen from the equilibrium phase diagram of Figure 5A that the solubility of Al in fcc-VN is almost zero, whereas in the PVD coatings, the solubility of Al in fcc-V1-xAlxN can be as high as x = 0.62. The maximum solubility of Al in VAlN coatings can be accurately predicted by calculating the formation enthalpies using first-principles calculations or the Gibbs free energies using the CALPHAD approach [Figure 5B]. Based on a surface diffusion kinetics simulation via the CALPHAD approach and first-principles calculations, and in particular, using only one set of high-throughput experiment data as input, the metastable phase formation diagram of the VAlN coating was established [Figure 5C] and validated using the experimental data obtained at different coating deposition power densities [Figure 5D-H].
Figure 5. Equilibrium and metastable phase diagrams for V-Al-N system: (A) equilibrium VN-AlN pseudobinary phase diagram; (B) Gibbs free energies of fcc and hexagonal close packed (hcp) V1-xAlxN solid-solution phases; (C) metastable VN-AlN phase formation diagrams calculated using experimental data at 550 °C and a power density of 2.3 W·cm-2 as inputs, and validated using the experimental data at power densities of (D) 2.3, (E) 4.6, (F) 6.8, (G) 1.2 and (H) 0.2 W·cm-2. Figure reproduced from Ref.[36] with permission from Elsevier.
Liu et al.[36] further revealed the linear relationship between the maximum solubility of Al and the residual stress in fcc-Ti1-xAlxN and fcc-V1-xAlxN coatings, adjusted the calculation model and predicted the metastable phase formation diagrams of TiAlN and VAlN coatings under the effect of compressive residual stress. In the metastable phase formation diagram established, the solubility of Al in V1-xAlxN, for example, extends to a range of 0.42 ≤ x ≤ 0.77, which covers all the experimental data available in the open literature (0.52 ≤ x ≤ 0.75) [Figure 6]. Hence, for the first time, a pressure-dependent theoretical model was developed and used to precisely predict the metastable phase formation diagram of ternary nitride coatings, which provides useful directions for the experimental efforts to control and extend the Al solubility in TM-Al-N coatings.
Figure 6. Calculated metastable VN-AlN phase formation diagrams with various deposition rates and stresses, compared with previous maximum Al solubility limit ranges of fcc-VAlN in the literature. Figure reproduced from Ref.[36] with permission from Elsevier.
The research progress made hitherto in the calculation of metastable phase formation diagrams suggests that, unlike the construction of a multicomponent equilibrium phase diagram, which relies on the CALPHAD approach to extrapolate from the binary system to the ternary, quaternary and multicomponent systems[51,52], the calculation model for the establishment of metastable phase formation diagrams requires consistent modification and verification to expand its adaptability.
Phase transformations in harsh service environments
The phase transformations that occur at the surfaces and interfaces of the materials serving in harsh environments may give rise to the degradation or enhancement of their properties. The attempts to understand the phase transformation in response to variations in temperature, stress, surrounding medium and so on based on thermodynamics and kinetics are valuable for the enrichment of phase diagram databases and the optimization of materials targeted for harsh service environments. In the following sections, research cases concerning the phase transitions of typical engineering materials serving in different application scenarios will be introduced.
Temperature
Quantitative metastable phase formation diagrams have been well established for cubic TM-Al-N coating systems using surface diffusion kinetics simulations[36,50], which pave the way for accurate control of phase constitutions during a PVD process. In the deposited TiAlN coating, for instance, the maximum solubility of Al in the fcc-TiAlN has been determined as 0.90, both computationally and experimentally[36]. Upon heating, however, metastable fcc-TiAlN may experience a non-equilibrium spinodal decomposition, which results in the formation of fcc-TiN-rich and fcc-AlN-rich nanosized domains, with the coating hardness enhanced[53]. A further increase in temperature gives rise to the phase transformation from the metastable fcc-AlN to the stable hexagonal close packed (hcp)-AlN, with a concomitant volume expansion and a corresponding property deterioration[54]. To delineate the temperature-induced microstructural evolution of cubic TM-Al-N coatings, Attari et al.[55] carried out a simulation of the isothermal annealing process of Ti1-x-yAlxZryN (x = 0.25-0.70) at 1200 °C. Using a phase-field method that integrates the Gibbs free energies derived from the CALPHAD approach with the atomic mobilities determined via key experiments, the simulation successfully predicted the non-equilibrium decomposition products that consist of fcc-AlN and fcc-Ti(Zr)N or fcc-AlN, fcc-ZrN and fcc-Ti(Zr)N, as well as the phase transformation from fcc-AlN to hcp-AlN. In addition, the microstructure evolved during the non-equilibrium phase transformation process was simulated [Figure 7A-C] and verified according to the results reported in the literature[56]. The agreement between the simulation and experimental results demonstrates that a combination of thermodynamics and kinetics could usefully interpret the evolutions of phase constitution and morphology during these temperature-induced non-equilibrium phase transformations.
Figure 7. Phase-field simulated microstructure of Ti1-x-0.05AlxZr0.05N annealed at 1200 °C for x = (A) 0.25, (B) 0.45 and (C) 0.70. The black color represents fcc-AlN, the white color represents fcc-TiN, while the grey color indicates fcc-ZrN. Figure reproduced from Ref.[55] with permission from Elsevier.
The selection of an appropriate fourth element to be added to the cubic TM-Al-N ternary system for improved thermal stability is an ongoing task for better surface protection in harsh service environments. A variety of candidate elements, including V[57], Ta[58], Zr[59], Y[60], Hf[61] and Nb[62], have been considered, but no clear consensus on a screening criterion has been reached. A precise delineation of the phase transformation pathways for TM-Al-X-N quaternary systems is crucial for establishing such a criterion. Recently, Zou et al.[63] performed key experiments coupled with first-principles calculations to study the addition of the noble metal element Ru on the phase structure and mechanical properties of TiAlN coatings. The results show that the minor hcp-AlN phase precipitates from the fcc-TiAlRuN solid solution as the Ru content increases. The simulation results confirm that the addition of Ru could reduce the solubility of AlN in TiAlN.
Zou et al.[63] further conducted a series of annealing tests to determine the spinodal decomposition temperatures of TiAlRuN and TiAlN coatings. It was found that the TiAlRuN coating starts to decompose at a higher temperature of 1000 °C compared to that of 900 °C for the TiAlN coating. According to the X-ray diffraction patterns, the decomposition of TiAlRuN gives rise to the formation of a metastable TiRuN phase, which further breaks down into Ru and TiN with increasing temperature. This observation follows the decomposition pathway predicted by first-principles calculations, as shown in Figure 8A, where TiAlRuN is more inclined to decompose into TiRuN and AlN thermodynamically. In addition, the role of Ru addition on the nanohardness of a TiAlN coating is revealed in Figure 8B, where a higher hardness value is attained at a moderate Ru concentration (Ti0.43Al0.50Ru0.07N) and further increase in Ru content results in a decline in hardness. The variation trend in coating hardness is consistent with the maximum solubility predicted by the simulation results. Thus, this work provides an example of the effectiveness of computational methods in rationalizing both the pathways of phase transformation and the consequent changes in thermal stability and mechanical properties.
Figure 8. (A) Separation enthalpies of Ti1-xAlxN, Ru1-xAlxN and five different decomposition pathways of Ti0.944-xAlxRu0.056N. (B) Hardness values of Ti0.44Al0.56N, Ti0.43Al0.50Ru0.07N and Ti0.34Al0.51Ru0.15N coatings as a function of annealing temperature. Figure reproduced from Ref.[63] with permission from Elsevier.
Stress
Multiple allotropes have been discovered in Si and phase transformations can give rise to alterations in its mechanical and optical properties[64,65]. Benefitting from advanced characterization technology, the stress-induced phase transformation can be in situ monitored using spectroscopy and electron microscopy equipped with a mechanical testing module[65]. For example, Zhang et al.[66] studied the stress-induced phase transition in single-crystal Si with a (100) crystallographic orientation using a nanoindentation test instrument under in situ transmission electron microscopy (TEM) observations. A Si-VI phase was observed to generate underneath the indentation impression at an applied load of 60 μN, while in other regions far from the indentation impression, the pristine Si-I phase remained unchanged. The deformation mechanism from the Si-I phase to the Si-VI phase was elucidated with the aid of high-resolution TEM and first-principles calculations. During the indentation, the Si-I phase suffers from both compressive and shear stresses; the purple and green atoms shown in Figure 9A are compressed vertically and integrated into the same atomic layer as a result of compression [Figure 9B]. Under the effect of shear stress, the blue and purple atoms rotate around the immobile green atoms, such that the Si-I phase transforms into the Si-VI phase when the rotation angle reaches 17.3° [Figure 9C]. In addition, the increment in the average potential energy is estimated as 0.434 eV and that in the average force exerted on each atom is 1.144 nN during the rotation process [Figure 9D].
Figure 9. First-principles calculations of (A) isometric and front views of a Si-I crystal structure under a diamond indenter and (B) a deformed crystal structure under compression. Inset in (B) shows red and blue top views taken from an isometric view of deformed Si-I under compression. First-principles calculations of (C) a rotated crystal structure under shear stress from the red and blue top views shown in the inset of (B). (D) Variations of average energy and force of an atom as a function of angle during the rotation process shown in (C). Inset in (D) shows the formation of Si-VI from Si-I after compression and rotation under a diamond indenter. Figure reproduced from Ref.[66] with permission from the Royal Society of Chemistry.
To examine the phase transition in Si under more severe stress conditions, Wang et al.[67] conducted high-speed grinding tests on single-crystal Si and studied its microstructural evolution after exposure to high external stresses. The stress-induced nanostructures consist of an amorphous region in the immediate vicinity of the top surface, followed by a new tetragonal phase, slip bands, twinning superlattices and eventually the Si single crystal. Using first-principles calculations, the phase transition mechanism from the Si-I phase to the new tetragonal phase was clarified. The atoms on the (111) crystallographic plane move towards the  orientation for a distance of
orientation for a distance of  and the two (111) planes then form an angle of 90° in such a way that a new tetragonal phase takes shape. As per the Peierls-Nabarro model[68], a minimum stress of 1.59 GPa is required to complete this transformation and this value is close to the stress estimated by the first-principles calculations (2.16 GPa). Thus, the integration of in situ characterization and computational methods could be an effective way to discover and rationalize stress-induced phase transformations in critical engineering materials.
and the two (111) planes then form an angle of 90° in such a way that a new tetragonal phase takes shape. As per the Peierls-Nabarro model[68], a minimum stress of 1.59 GPa is required to complete this transformation and this value is close to the stress estimated by the first-principles calculations (2.16 GPa). Thus, the integration of in situ characterization and computational methods could be an effective way to discover and rationalize stress-induced phase transformations in critical engineering materials.
Surrounding medium
In marine engineering applications, the anti-bacterial and anti-fouling properties of materials should be considered as a priority to maintain the functionality of machinery, such as underwater vehicles[69,70]. In this context, developing multi-functional protective coatings becomes a challenging but imperative task for modern ocean explorations. Zhu et al.[71] synthesized TiSiN/Ag multilayered coatings using a multi-arc ion plating technique and examined their anti-bacterial properties. The coating system exhibited a maximum hardness value of 33 GPa and an inhibition ratio of 99.99% towards both E. coli and B. subtilis after 24 h. It was found that the TiSiN sublayer consisting of TiN nanocrystals and a Si3N4 amorphous phase could act not only as a barrier but also as a microchannel for sluggish diffusion and the release of Ag atoms constantly towards the surface.
Another benefit originating from the Ag diffusion could be the self-healing effect on the cracks generated in the coating system. Zhu et al.[72] further studied the self-healing behavior of TiSiN/Ag multilayered coatings upon oxidation using first-principles calculations, molecular dynamics simulations and key experiments. The results suggest that the presence of O2 induces the oxidation of TiN and Si3N4 phases in the top surface layer and Ag atoms readily diffuse outwards along the phase boundaries between the TiN nanocrystals and the Si3N4 amorphous phase simultaneously [Figure 10A-D], both of which contribute to the self-healing of surface and internal cracks, as well as the maintenance of anti-corrosion and anti-fouling properties. Therefore, theoretical studies that rely on a coordination of thermodynamics and kinetics could lay an important basis for the research and development of novel multi-functional protective coatings.
Figure 10. Diffusional behavior of Ag atoms simulated using molecular dynamics for (A) 0, (B) 100, (C) 250 and (D) 400 fs. Figure reproduced from Ref.[72] with permission from John Wiley & Sons.
Temperature-stress interactions
Ceramic-metal composites represent a major category of hard yet tough materials and are widely used in critical engineering applications, including metal cutting, offshore mining, rock drilling and so on, where working surfaces interact with an oxidizing medium under high temperature and stress conditions[73,74]. A comprehensive understanding of surface damage mechanisms is therefore a prerequisite for the further optimization of the materials.
Lou et al.[37] selected TiC-γFe as a model system to delineate the wear mechanism when subjected to temperature and atmosphere variations. The results show that there exists a critical temperature of ~125 °C at which the wear mechanism transition occurs [Figure 11]. Below this temperature, hardness governs the wear behavior. The oxygen-assisted surface decarburization of TiC particles during the sliding process was identified for the first time using micro-Raman spectroscopy, with the thermodynamics of this phase transformation elucidated using the CALPHAD approach and the resulting hardness reduction clarified using first-principles calculations. Above the critical temperature, however, the deformation compatibility between ceramic particles and metallic binders becomes a dominant factor that affects the wear properties. The sliding-induced formation of a continuous tribolayer consisting of nano Ti oxides on the surface of TiC particles was characterized by in situ TEM, while the toughness improvement benefiting from the tribolayer formation was determined both experimentally using indentation fracture toughness measurements and computationally using first-principles calculations. Overall, with the aid of in situ characterization and computational methods, this study suggests that the wear resistance of ceramic-metal composites is sensitive to temperature, stress and oxidizing medium. The wear transition temperature depends on, but is not limited to, factors including hardness, toughness and deformation compatibility.
Figure 11. Temperature-induced wear transition in the ceramic-metal (TiC-γFe) composite system. A critical temperature of ~125 °C at which the wear mechanism transition occurs was determined, where phase transformations, including surface decarburization and oxidation, were investigated using in situ TEM and interpreted using the CALPHAD approach and first-principles calculations. Figure reproduced from Ref.[37] with permission from Elsevier.
As the research cases pertaining to different application scenarios show, unravelling the phase transformation at the surfaces and interfaces of materials based on a coordination of thermodynamic and kinetic simulations, in addition to in situ material characterization, with the individual roles of stress, temperature and surrounding medium isolated, is conducive to promoting better solutions to the surface protection problems in harsh service environments.
Phase diagram database-guided materials optimization
The concepts of the materials genome and materials informatics have highlighted that the highly efficient optimization of critical engineering materials (and coatings) requires explicit relationships established between processing, structure and properties. Phase diagrams that can precisely describe the phase constitution at specific conditions, i.e., temperature, pressure and composition, may potentially predict service properties and are therefore regarded as powerful tools in this process. Thus, applying reasonable calculation models, instead of using a large quantity of experimental data to describe the phase relations and demarcate the phase boundaries, is deemed necessary for high-efficiency materials optimization. The following sections introduce recent research progress related to the successful fulfillment of phase diagram database-guided materials optimization.
Wear-resistant ceramic coatings
Amelioration of the wear resistance of coatings through the incorporation of additional elements in mature coating systems, such as the Ti-Al-N ternary system, is a common method in the research and development of coating materials. However, this strategy does not adequately circumvent some intrinsic weaknesses in the system, for example, the inherent brittleness in nitride coatings[75]. Thus, exploring alternative methods to engineer hard yet tough ceramic coatings based on materials databases is a necessity.
For this purpose, Emmerlich et al.[76] proposed a series of selection criteria for candidate coating systems: (1) a bulk modulus (B) to shear modulus (G) ratio (B/G) > 1.75; (2) a positive Cauchy pressure; (3) a congruent melting point; (4) a preferable phase stability; and (5) a high Young’s modulus (E). Among these parameters, the elastic moduli (B, G and E) and the Cauchy pressure can be well predicted by first-principles calculations, while the congruent melting point and phase stability can be judged from the phase diagrams established using the CALPHAD approach. Through the computational screening of a wide variety of ceramic material systems, Mo2BC was found to possess a high stiffness combined with moderate ductility and meets all the aforementioned criteria. Specifically, nanolaminated Mo2BC exhibits a B/G ratio of 1.75 and a Cauchy pressure of 43 GPa, compared to a B/G ratio of 1.44 and a Cauchy pressure of -40 GPa for TiAlN. Mo2BC melts congruently at temperatures above 2500 °C, whereas TiAlN reveals spinodal decomposition below 1000 °C. In addition, the E value of Mo2BC is estimated as 470 GPa, comparable to that of TiAlN (400-500 GPa). The nanohardness value of the PVD deposited Mo2BC coating was subsequently measured as 29 ± 2 GPa, which is similar to that of TiAlN (~30 GPa). During the indentation process, no apparent sign of brittle fracture was noted, suggesting good deformation tolerance of the Mo2BC coating. Hence, this study exhibits a property-oriented all-round design strategy for wear-resistant ceramic coatings (as shown in Figure 12), which can act as a reference to the future exploration of new coating systems.
Figure 12. Computational screening strategy of coating materials based on the CALPHAD approach and first-principles calculations for the development of hard yet tough ceramic coatings.
Another possible method to engineer coating systems with improved ductility could be the construction of multilayered architectures at the nanoscale. By assembling two different coating materials alternately, the nano-multilayered coatings may exhibit enhanced properties that outperform each of the component layers (i.e., the sublayers). Xu et al.[77] studied the optimal modulation ratio for constructing coherent interface structures in TiAlN/MeN (Me = Ti or Zr) using first-principles calculations and key experiments. The energy difference (ΔE) between TiAlN/MeN and the single layered one, as well as the work of separation (Wsep) corresponding to the introduction of the interface in comparison to two separate slab structures, was calculated at different modulation ratios (tTiAlN:tMeN = 4:1, 3:2, 2:3 and 1:4). The results show that the TiAlN/TiN multilayered coating system can readily form coherent interfaces between the sublayers, regardless of the varied modulation ratios, whereas the interfacial structure in the TiAlN/ZrN coating system depends strongly on the modulation ratio. To be specific, the TiAlN/ZrN coating exhibits a lower ΔE but a higher Wsep at tTiAlN:tZrN = 1:4 [Figure 13A], suggesting a higher stability of the coherent interface structure at this modulation ratio. These simulation results are in agreement with the TEM observations made on the TiAlN/MeN multilayered coatings [Figure 13B]. Thus, this study provides a vivid example of the usefulness of computational methods in designing multilayered architectures in nitride coatings.
Figure 13. (A) First-principles calculated energy difference (ΔE) and work of separation (Wsep) as a function of modulation ratio (tTiAlN:tMeN) for TiAlN(001)/TiN(001) and TiAlN(001)/ZrN(001). (B) Cross-sectional TEM micrographs showing the interfacial structures in TiAlN/MeN multilayered coatings with different modulation ratios. Figure reproduced from Ref.[77] with permission from Elsevier.
In addition to PVD, chemical vapor deposition (CVD) is an equally important coating deposition technique that is extensively used in industrial applications[78]. To optimize the parametric variables, e.g., temperature, gas pressure and flow rate, for the CVD process, Qiu et al.[79,80] selected a TiSi(C)N coating as a model system and considered the precursors that are comprised of TiCl4-SiCl4(-CH3CN)-NH3-H2. Using the CALPHAD approach, a series of parameter-dependent phase diagrams was established. As shown in Figure 14A, at a constant pressure of 6 kPa, for example, the phase formation sequence can be listed as TiN+Si3N4 → TiN+Si3N4+SiC → SiC+TiN → TiC+SiC+TiN following a temperature increase from 800 to 1400 K. In contrast, when the temperature is fixed at 1123 K, the phase formation sequence is in the opposite direction when the pressure increases from 2 to 20 kPa. It is also noted from Figure 14B that for a deposition temperature range of 1034-1083 K and the mole fraction of SiCl4 that is within 0.011, the TiC+Si3N4 two-phase, the TiC+Si3N4+SiC ternary-phase and the TiN+TiC+Si3N4+SiC quaternary-phase regions are relatively narrow, implying the importance of precisely controlling the deposition parameters. Eventually, with the deliberately selected parameters, the co-existence of the amorphous SiCxNy phase and the nanocrystalline TiCxNy phase was realized in the CVD nanocomposite coating structure.
Figure 14. Calculated phase diagrams of TiSiCN depending on different parameters: (A) temperature and pressure; (B) temperature and mole fraction of SiCl4 (CH3CN). (C) CFD simulated temperature contours in an industrial-scale CVD furnace. Figure reproduced from Refs.[79,81] with permission from Elsevier.
In parallel with the endeavors to establish parameter-dependent CVD phase diagrams, Qiu et al.[81] also conducted computational fluid dynamics (CFD) calculations for moderate-temperature Ti(C,N) coatings to understand the fluid behavior of gases in a CVD process. CFD calculations can provide valuable information on the distributions of temperature, gas concentration and deposition rate in an industrial scale CVD furnace ahead of the actual coating deposition. Using the temperature contours simulated in Figure 14C as an example, it can be seen that the temperature rises from the bottom tray to the top one, while on the same tray it also increases from the internal locations to the external ones (with a temperature difference of < 10 K). The simulation results are in reasonable agreement with the experimental evidence. Thus, based on the CALPHAD and CFD approaches, a holistic design strategy including the selection of deposition parameters and the optimization of coating structures has been proposed for CVD coatings.
Co-based superalloys
Superalloys, including Ni-, Co- and Fe-based alloys, represent the foremost high-temperature structural materials or hardfacing coatings employed in nuclear power generation and the automotive and aerospace industries[82]. Theoretically, Co-based superalloys have excellent potential to outperform their widely-used Ni-based counterparts in terms of high-temperature capability, as they possess a higher solidus temperature. Notwithstanding, a lack of the strengthening γ’ phase is a dauting challenge to the development of Co-based superalloys with superior high-temperature strength.
Recently, Ruan et al.[83] employed a machine learning algorithm combined with the CALPHAD approach to seek for a novel Co-based superalloy system with a wide γ+γ’ two-phase region. The property-related parameters, i.e., the solvus temperature (Tγ’-solvus) and the area fraction (Aγ’-area fraction) of γ’ precipitates, have been predicted using a random forest algorithm based on datasets collected from the literature, while grain-boundary segregation has been subtly controlled according to the thermodynamic calculation results based on a Ni-based superalloys database (TTNI8). After a thorough evaluation of Tγ’-solvus, Aγ’-area fraction and phase constitution (as shown in Figure 15A and B), a Co-12V-2Ta (in at.%) system consisting of the cuboidal γ’ phase homogeneously distributed in the γ matrix (as shown in Figure 15C and D) was fabricated and used as the master alloy. Through the further incorporation of a strong γ’-forming element (Ti), a Co-12V-2Ta-2Ti superalloy with enhanced high-temperature strength and reduced mass density, compared with the well-known Co-9Al-9.8W alloy system, was successfully attained. Thus, this work shows the effectiveness of jointly using the machining learning and CALPHAD methods based on multi-databases to accelerate the optimization process of critical material systems with properties beyond their limits.
Figure 15. (A) Solvus temperature (Tγ’-solvus) and (B) area fraction (Aγ’-area fraction) of γ’ phase in the Co-V-Ta alloy annealed at 800 °C for 600 h, as predicted using machine learning, with the γ and γ’ phase boundaries demarcated in the isothermal section of the Co-V-Ta system at 800 °C established using the CALPHAD approach. (C) Dark-field image and (D) selected area diffraction pattern obtained from the γ+γ’ region in the Co-V-Ta alloy annealed at 800 °C for 648 h. Figure reproduced from Ref.[83] with permission from Elsevier.
Ultrafine cemented carbides
WC-Co-based cemented carbides have been widely used as tool materials in cutting, milling, turning and drilling applications since they were first developed in the 1920s[84]. Among the different types of cemented carbides, ultrafine grain WC-Co with enhanced mechanical properties has received significant attention from both academia and industry[84,85]. The incorporation of a grain growth inhibitor, for example, Cr3C2, VC, NbC or TaC, is a viable method to fabricate cemented carbides with refined WC particles[86]. However, a side effect induced by inhibitor addition could be the formation of an inhomogeneous microstructure that shows segregation of the inhibitors added[87].
To eliminate microstructural inhomogeneity in ultrafine cemented carbides, Li et al.[88] selected WC-Co-Ta as a model system, designed and validated its optimal composition via the CALPHAD approach and key experiments. According to the phase diagram established [Figure 16A] and the calculated mole percent of the (Ta,W)C cubic phase [Figure 16B] at the sintering temperature (1410 °C), three typical compositions with different C concentrations within the favorable region were selected. The results indicate that at the highest C concentration (5.52 wt.%), a large quantity of (Ta,W)C cubic phase remains undissolved in liquid Co at the sintering temperature and is evenly dispersed across the microstructure. During cooling, the dissolved Ta atoms precipitate from the oversaturated binder phase onto the undissolved cubic phase. On this basis, the segregation of the (Ta,W)C cubic phase is avoided in WC-Co-Ta (5.52 wt.% C) and enhanced hardness and transverse rapture strength are simultaneously realized. Hence, this work shows the possibility of microstructural and property optimization via the precise control of the minor element concentration as per the phase diagram database.
Figure 16. Development of ultrafine WC-Co-based cemented carbides according to the thermodynamically calculated (A) phase diagram and (B) mole percent of (Ta,W)C cubic phase in the WC-10Co-0.5Ta cemented carbides (at 1410 °C). Three dashed lines indicate the carbon contents of the samples synthesized. L = liquid, η = M6C, γ = Co binder, δ = cubic phase and C = graphite phase. Figure reproduced from Ref.[88] with permission from Elsevier.
Nuclear cladding materials
Nuclear reactors represent extreme environments with severe working conditions where materials are required to bear long-time irradiation, high temperatures and strong corrosive media[89]. Since the occurrence of the Fukushima Daiichi nuclear disaster in 2011, accident tolerant fuel (ATF) cladding materials, which could help to retard catastrophic nuclear accidents, have been in urgent demand[90]. Silicon carbide (SiC) ceramics are promising ATF cladding materials for use in the nuclear industry due to their excellent thermal and mechanical properties, in addition to the low induced radioactivity[91]. However, a major technical difficulty lies in the fabrication of SiC ceramics, which normally requires high temperature (~2000 °C) and high pressure (~50 MPa) to achieve full densification[92]. A viable method to possibly reduce the sintering temperature is the employment of suitable sintering aids[93,94]. For instance, Shao et al.[95]in situ synthesized powders that possess a SiC-Y3Si2C2 core-shell structure using a molten salt technique and found that a Y3Si2C2 sintering aid facilitates a nearly full densification of SiC ceramics (with a 99.5% relative density) at a decreased temperature of 1600 °C.
Xu et al.[96] studied the thermodynamics underlying this temperature reduction by assessing the Y-SiC vertical section [Figure 17A] of the Y-Si-C ternary system using the CALPHAD approach aided with first-principles calculations. It was noted that Y3Si2C2 co-exists with SiC in a two-phase equilibrium region up to a temperature of 1100 °C, while a liquid phase emerges at temperatures above 1560 °C. Thus, it was rational to conclude that during the sintering of SiC, the Y3Si2C2 shell reacts with the SiC core and transforms into a liquid state at 1600 °C, such that the grain size may be refined at the core-shell interface and the SiC ceramics are fully densified under the effect of the pressure exerted concurrently.
Figure 17. Calculated vertical sections along the composition of SiC:RE = 1:1 for (A) Y-Si-C, (B) Dy-Si-C, (C) Pr-Si-C and (D) La-Si-C. Temperature of the reaction between RE3Si2C2 and SiC at which the liquid phase starts to form is labelled in each diagram. Figure reproduced from Refs.[96,98,99] with permissions from Elsevier and John Wiley & Sons.
The successful development of Y3Si2C2 as a sintering aid has stimulated the exploration for more efficient aids based on rare earth (RE)-containing metallic compounds, RE3Si2C2 (RE = La-Nd, Sm and Gd-Tm)[97]. Xu et al.[98,99] further compared the effectiveness of Dy, Pr and La incorporated sintering aids on lowering the densification temperature of SiC by examining the vertical sections of RE-SiC using the CALPHAD approach coupled with first-principles calculations. It can be seen from the phase diagrams that the additions of Dy [Figure 17B], Pr [Figure 17C] and La [Figure 17D] reduce the reaction temperature of RE3Si2C2 to 1433, 1148 and 810 °C, respectively. The calculations of phase transformation temperatures demonstrate that using different types of RE elements to form a core-shell structure with the SiC particles could be a feasible approach for realizing the densification of SiC ceramics at lower sintering temperatures.
Another candidate ATF cladding material system could be the oxidation-resistant Fe-Cr-Al[100], although its industrial application has been hindered so far, owing to the formation of the Cr-rich brittle α’ phase at temperatures slightly below 475 °C[101,102]. To provide theoretical guidance for detrimental phase prevention, Chang et al.[103] optimized the isothermal section of the Fe-Cr-Al system at 475 °C [Figure 18A], as well as the phase diagram for the Fe-rich corner that is comprised of an α phase region and an α+α’ two-phase equilibrium region [Figure 18B] using the CALPHAD approach aided by first-principles calculations and high-throughput experiments. The calculation results are in good agreement with the experimental data from annealing tests conducted at 475 °C. To further investigate the temperature-dependent precipitation behavior of the α’ phase from the α phase, Chang et al.[103] selected the typical service temperature (320 °C) of nuclear cladding materials and calculated the isothermal section of the Fe-Cr-Al system [Figure 18C]. The calculation results are well supported by the experimental data from irradiation tests performed at 320 °C [Figure 18D]. Finally, by means of phase diagrams calculated at different temperatures (475, 450, 425, 400, 375, 350 and 325 °C), the migration of the α/α+α’ phase boundary towards the Al-rich corner induced by the temperature decrease was captured [Figure 18D].
Figure 18. Calculated phase diagrams of the Fe-Cr-Al system using the CALPHAD approach: (A) isothermal section at 475 °C; (B) Fe-rich corner at 475 °C, where the solid symbols indicate α+α’ phases, the open ones designate the single α phase and the sphere symbols are the experimental data (α+α’ phases) from the FeCrAl samples irradiated at ~320 °C; (C) isothermal section at 320 °C; (D) Fe-rich corner at 320 °C together with the ones at 475, 450, 425, 400, 375, 350 and 325 °C, where the experimental data from (A) are re-labeled to adjust the phase relations at 320 °C. Figure reproduced from Ref.[103] with permission from Elsevier.
According to the phase diagram database, increasing the Al concentration may inhibit the generation of the α’ phase and benefit the oxidation resistance as well, but the materials with excessive Al are difficult to weld and machine. To efficiently demarcate the optimal composition range of the Fe-Cr-Al ternary system, Chang et al.[103] constructed the composition-structure-property relationship diagram of Fe-Cr-Al at 320 °C [Figure 19]. The suggested composition range as outlined by the dotted lines is determined considering three main facets, namely, the α single phase region, the melting point, as well as the mechanical properties. The composition range can be further narrowed down to the area demarcated by the dash lines, considering the welding property at the same time. Thus, utilizing high-throughput experiments coupled with the CALPHAD approach and first-principles calculations, an optimal composition range for the nuclear cladding Fe-Cr-Al system has been proposed, which can be used as references for the selection of explicit material compositions.
Figure 19. Development of composition-structure-property relationships for Fe-Cr-Al ATF cladding materials with a proposed composition range based on the calculated phase diagram at 320 °C. Figure reproduced from Ref.[103] with permission from Elsevier.
Corrosion-resistant NiXAlY materials
The M-Cr-Al-Y (M = Ni, Co or Fe) quaternary system represents the state-of-the-art hot-corrosion resistant coating system being used either directly on gas turbine blades or as the bond coat in thermal barrier coating systems[104,105]. The excellent hot-corrosion resistance of M-Cr-Al-Y coatings arises from the formation of continuous and dense oxide films that are mainly comprised of Al2O3 and Cr2O3 on their surface[106]. As such, the stability of these oxide films becomes a vital factor that determines the durability of these coatings in harsh environments. It was reported[107] that in high-temperature salt spray environments, Al2O3 can barely react with NaCl and H2O as this reaction is not thermodynamically favorable. In contrast, Cr2O3 is apt to spallation as a result of the chemical reaction with NaCl and H2O at temperatures ranging between 400 and 700 °C[108,109]. Therefore, the substitution of Cr with other elements is essential to improve the adaptability of a coating to marine salt spray environments while maintaining similar high temperature properties.
Xu et al.[38,110] comprehensively considered the chemical activity and phase formation ability of candidate elements, and selected Si, Ta, Mo, Cu and Ti for designing the novel Ni-X-Al-Y quaternary system. Using the Ni-Si-Al-Y system as an example, Xu et al.[38,110] critically assessed the Al-Ni-Si, Al-Ni-Y, Al-Si-Y, Ni-Si-Y ternary systems and subsequently developed the Al-Ni-Si-Y quaternary phase diagram database. To examine the accuracy of the database, three representative samples with explicit compositions, namely, #1-Ni-12Al-1Si-1Y, #2-Ni-12Al-3Si-1Y and #3-Ni-12Al-5Si-1Y (in wt.%), were prepared as per the isothermal section of the Al-Ni-Si-Y quaternary system at 750 °C [Figure 20A]. The phase constitutions depicted in the calculated phase diagram are in line with the experimental results where a two-phase structure consisting of γ’-Ni3Al and Ni5Y was identified in sample #1 and a ternary-phase structure comprised of γ’-Ni3Al, β-NiAl and Ni5Y was detected in samples #2 and #3. The changes in phase fractions in sample #2 along with the temperature rise (up to 1800 °C) calculated from the phase diagram database are shown in Figure 20B. According to the calculation results, minor β-NiAl and Ni5Y phases would precipitate from the γ’-Ni3Al matrix at 1300 °C. This prediction is well supported by the annealing test (at 1300 °C for 24 h) result, as shown in the inset of Figure 20B. Therefore, by determining reasonable thermodynamic descriptions of the binary and ternary sub-systems, a reliable Al-Ni-Si-Y quaternary phase diagram database was successfully constructed via extrapolation.
Figure 20. Calculated Al-Ni-Si-Y quaternary phase diagrams: (A) isothermal section in the Ni-rich corner at 750 °C; (B) variation of phase fraction along with increasing temperature for sample #2 Ni-12Al-3Si-1Y. The inset in (B) shows the microstructure of sample #2 after annealing at 1300 °C for 24 h, in which the eutectic structure consists of γ’-Ni3Al and β-NiAl. Figure reproduced from Ref.[38] with permission from Elsevier.
Utilizing this database, Xu et al.[38] finally established the composition-structure-property relationship diagram and demarcated the optimal composition range of the Ni-Si-Al-Y system based on the isothermal sections at both 750 and 1140 °C [Figure 21]. In this specific composition range, the material system is expected to exhibit high strength combining with excellent resistance to high temperature oxidation and corrosion.
Figure 21. Development of the hot-corrosion resistant Ni-Si-Al-Y quaternary system: composition-structure-property relationships based on the calculated phase diagrams at 750 and 1140 °C. The proposed composition range may possess a combination of high strength, toughness, as well as excellent high-temperature oxidation and corrosion resistance. Figure reproduced from Ref.[38] with permission from Elsevier.
As the abovementioned research cases show, phase diagram databases play a critical role in the screening of candidate elements and the determination of the concentration of major or minor constituents for a wide variety of material categories and are expected to be prioritized during the materials optimization targeted for surface protection in harsh service environments.
Concluding remarks
The development and optimization of coating materials for elongated durability under harsh service environments are challenging but imperative tasks. Novel coating materials with ever-increasing complexity in constitution and structure make computational methods indispensable to materials design. In particular, the continuous renovation of the conventional CALPHAD approach through the coupling with other simulation methods (such as first-principles calculations, molecular dynamics, phase-field method and so on) and key experiments has gradually realized a novel materials design strategy. This renovation relies on the CALPHAD in combination with other computational methods, high-throughput experiments and materials databases. Alternatively, data-driven materials research, referred to as materials informatics, which harnesses data mining and statistical methods in conjunction with physically-driven models to capture the physical essence from materials databases, also shows great potential in reliable performance prediction and materials recommendation[83,111,112]. In general, the idea and methodology of the materials design strategy presented in this work are within the scope of integrated computational materials engineering and the Materials Genome Initiative, both of which are in line with the scientific connotation of materials informatics[113] and are committed to saving time and efforts in the research and development of novel engineering materials.
Continuous modifications on the research scheme and calculation models are still in high demand, albeit some research advances have already been made. To develop robust surfaces with self-adaptability to the variations of temperature, stress and surrounding medium, several critical scientific problems need to be addressed in future research:
A quantitative calculation model for predicting the metastable phase formation in a multicomponent coating system (with five or more elements) remains to be developed;
The feasibility and reliability of the calculation method remain to be ascertained for multicomponent coatings (e.g., high entropy alloy coatings) that potentially consist of various metastable phases;
A quantitative description of the formation and stability of amorphous phases in the coating structure is still absent and remains to be established;
A quantitative relationship between the phase formation and the coating deposition parameters (e.g., pressure, bias voltage and so on) remains to be built;
A trustworthy prediction of critical materials properties (besides thermal stability) remains to be fulfilled based on computational methods.
Declarations
Authors’ contributionsWriting: Lou M, Xu K, Chen L, Hong C, Yuan Y
Review and editing: Lou M, Du Y, Chang K
Resources, supervision, and project administration: Lou M, Xu K, Du Y, Du Y, Chang K
Availability of data and materialsNot applicable.
Financial support and sponsorshipThe financial support from National Natural Science Foundation of China (51971235), State Key Laboratory of Powder Metallurgy, Central South University, Changsha, China, National Natural Science Foundation of China (Nos. 52101026 & 52101108), China Postdoctoral Science Foundation (2021M693250), Natural Science Foundation of Zhejiang Province (LQ20E010004), and Ningbo 3315 Innovation Team (Nos. 2019A-18-C & 2020A-03-C) is gratefully acknowledged.
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2021.
REFERENCES
1. Cattant F, Crusset D, Féron D. Corrosion issues in nuclear industry today. Mater Today 2008;11:32-7.
2. Williams JC, Starke EA. Progress in structural materials for aerospace systems. Acta Mater 2003;51:5775-99.
3. Wood RJ. Erosion-corrosion interactions and their effect on marine and offshore materials. Wear 2006;261:1012-23.
4. Allen T, Busby J, Meyer M, Petti D. Materials challenges for nuclear systems. Mater Today 2010;13:14-23.
5. Batchelor AW, Lam LN, Chandrasekaran M. Materials degradation and its control by surface engineering. 3rd ed. London: Imperial College Press; 2011.
6. Abu-odeh A, Galvan E, Kirk T, et al. Efficient exploration of the High Entropy Alloy composition-phase space. Acta Mater 2018;152:41-57.
7. Miracle D, Senkov O. A critical review of high entropy alloys and related concepts. Acta Mater 2017;122:448-511.
8. Chen X, Han Z, Li X, Lu K. Lowering coefficient of friction in Cu alloys with stable gradient nanostructures. Sci Adv 2016;2:e1601942.
9. Xie Z, Hoffman M, Munroe P, Bendavid A, Martin P. Deformation mechanisms of TiN multilayer coatings alternated by ductile or stiff interlayers. Acta Mater 2008;56:852-61.
10. Xiong J, Zhang T, Shi S. Machine learning of mechanical properties of steels. Sci China Technol Sci 2020;63:1247-55.
11. Xiong J, Shi S, Zhang T. A machine-learning approach to predicting and understanding the properties of amorphous metallic alloys. Mater Des 2020;187:108378.
12. Ramakrishna S, Zhang T, Lu W, et al. Materials informatics. J Intell Manuf 2019;30:2307-26.
13. Du Y, Li K, Zhao P, et al. Integrated computational materials engineering (ICME) for developing aluminum alloys. J Aeronaut Mater 2017;37:1-17. (in Chinese)
14. Zhang W, Du Y, Peng Y, et al. Integrated computational materials engineering (ICME) for developing the cemented carbides. Mater Sci Technol 2016;24:1-28. (in Chinese)
15. Li B, Du Y, Qiu L, et al. Shallow talk about integrated computational materials engineering and materials genome initiative: ideas and practice. Mater China 2018;37:264-83. (in Chinese)
16. de Pablo JJ, Jackson NE, Webb MA, et al. New frontiers for the materials genome initiative. npj Comput Mater 2019;5:41.
17. Curtarolo S, Hart GL, Nardelli MB, Mingo N, Sanvito S, Levy O. The high-throughput highway to computational materials design. Nat Mater 2013;12:191-201.
18. Arslan HK, Shekhah O, Wohlgemuth J, Franzreb M, Fischer RA, Wöll C. High-throughput fabrication of uniform and homogenous MOF coatings. Adv Funct Mater 2011;21:4228-31.
19. Ludwig A. Discovery of new materials using combinatorial synthesis and high-throughput characterization of thin-film materials libraries combined with computational methods. npj Comput Mater 2019;5:70.
20. White P, Smith G, Harvey T, et al. A new high-throughput method for corrosion testing. Corros Sci 2012;58:327-31.
21. Shi Y, Yang B, Rack PD, Guo S, Liaw PK, Zhao Y. High-throughput synthesis and corrosion behavior of sputter-deposited nanocrystalline Al (CoCrFeNi)100- combinatorial high-entropy alloys. Mater Des 2020;195:109018.
22. Zeng Y, Liu Y, Min Q, et al. Diffusion coefficients and atomic mobilities in fcc Ni-Cu-Mo alloys: experiment and modeling. Calphad 2020;71:102209.
23. Mao SS. High throughput combinatorial screening of semiconductor materials. Appl Phys A 2011;105:283-8.
25. Kaufman L, Bernstein H. Computer calculation of phase diagrams: with special reference to refractory metals. New York: Academic Press; 1970.
26. Liu Y, Zhang C, Du C, et al. CALTPP: a general program to calculate thermophysical properties. J Mater Sci Mater Med 2020;42:229-40.
28. Szabó B, Babuška I. Introduction to finite element analysis: Formulation, verification and validation. West Sussex: John Wiley & Sons; 2011.
30. Liu Z. First-principles calculations and CALPHAD modeling of thermodynamics. J Phase Equilib Diffus 2009;30:517-34.
31. Du Y, Sundman B. Thermophysical properties: key input for ICME and MG. J Phase Equilib Diffus 2017;38:601-2.
32. Du J, Jindal V, Sanders A, Ravi Chandran K. CALPHAD-guided alloy design and processing for improved strength and toughness in Titanium Boride (TiB) ceramic alloy containing a ductile phase. Acta Mater 2019;171:18-30.
33. Zhou J, Zhong J, Chen L, et al. Phase equilibria, thermodynamics and microstructure simulation of metastable spinodal decomposition in c-Ti1-xAlxN coatings. Calphad 2017;56:92-101.
34. Povoden-karadeniz E, Lang P, Warczok P, Falahati A, Jun W, Kozeschnik E. CALPHAD modeling of metastable phases in the Al-Mg-Si system. Calphad 2013;43:94-104.
35. Chang K, Lou M, Xu K, Chen L, Yuan Y. Phase diagram, phase transformation and materials development of coatings served in harsh environments. Mater China 2021;40:401-16. (in Chinese)
36. Liu S, Chang K, Music D, et al. Stress-dependent prediction of metastable phase formation for magnetron-sputtered V1-xAlxN and Ti1-x AlxN thin films. Acta Mater 2020;196:313-24.
37. Lou M, Chen X, Xu K, et al. Temperature-induced wear transition in ceramic-metal composites. Acta Mater 2021;205:116545.
38. Xu K, Chang K, Yu M, Zhou D, Du Y, Wang L. Design of novel NiSiAlY alloys in marine salt-spray environment: Part II. Al-Ni-Si-Y thermodynamic dataset. J Mater Sci Mater Med 2021;89:186-98.
39. Grovenor C, Hentzell H, Smith D. The development of grain structure during growth of metallic films. Acta Metall 1984;32:773-81.
40. Einstein A. Elementare Theorie der Brownschen Bewegung. Z Elektrotech Elektrochem 1908;14:235-9.
42. Saksena A, Chien YC, Chang K, et al. Metastable phase formation of Pt-X (X=Ir, Au) thin films. Sci Rep 2018;8:10198.
43. Chang K, to Baben M, Music D, Lange D, Bolvardi H, Schneider JM. Estimation of the activation energy for surface diffusion during metastable phase formation. Acta Mater 2015;98:135-40.
44. Chang K, Music D, To Baben M, Lange D, Bolvardi H, Schneider JM. Modeling of metastable phase formation diagrams for sputtered thin films. Sci Technol Adv Mater 2016;17:210-9.
45. Wang SQ, Chen L, Yang B, et al. Effect of Si addition on microstructure and mechanical properties of Ti-Al-N coating. Int J Refract Metals Hard Mater 2010;28:593-6.
46. Alat E, Motta AT, Comstock RJ, Partezana JM, Wolfe DE. Multilayer (TiN, TiAlN) ceramic coatings for nuclear fuel cladding. J Nucl Mater 2016;478:236-44.
47. Karimi Aghda S, Music D, Unutulmazsoy Y, et al. Unravelling the ion-energy-dependent structure evolution and its implications for the elastic properties of (V,Al)N thin films. Acta Mater 2021;214:117003.
48. Paldey S, Deevi S. Single layer and multilayer wear resistant coatings of (Ti,Al)N: a review. Mater Sci Eng A Struct Mater 2003;342:58-79.
49. Spencer P, Holleck H. Application of a thermochemical data bank system to the calculation of metastable phase formation during PVD of carbide, nitride and boride coatings. High Temp Sci 1989;27:295-309.
50. Liu S, Chang K, Mráz S, et al. Modeling of metastable phase formation for sputtered Ti1-xAlxN thin films. Acta Mater 2019;165:615-25.
51. Xu K, Liu S, Du Y, Dreval L, Cai G, Jin Z. Thermodynamic investigation of the Mg-Ni-Zn system by experiments and calculations and its application. J Alloys Compd 2019;784:769-87.
52. Chen L, Zhang Z, Huang Y, et al. Thermodynamic description of the Fe-Cu-C system. Calphad 2019;64:225-35.
53. Mayrhofer PH, Hörling A, Karlsson L, et al. Self-organized nanostructures in the Ti-Al-N system. Appl Phys Lett 2003;83:2049-51.
54. Endrino J, Århammar C, Gutiérrez A, et al. Spectral evidence of spinodal decomposition, phase transformation and molecular nitrogen formation in supersaturated TiAlN films upon annealing. Acta Mater 2011;59:6287-96.
55. Attari V, Cruzado A, Arroyave R. Exploration of the microstructure space in TiAlZrN ultra-hard nanostructured coatings. Acta Mater 2019;174:459-76.
56. Lind H, Pilemalm R, Rogström L, et al. High temperature phase decomposition in TixZryAlzN. AIP Adv 2014;4:127147.
57. Kutschej K, Mayrhofer P, Kathrein M, Polcik P, Mitterer C. A new low-friction concept for Ti1-xAlxN based coatings in high-temperature applications. Surf Coat Technol 2004;188-189:358-63.
58. Sui X, Li G, Jiang C, Yu H, Wang K, Wang Q. Effect of Ta content on microstructure, hardness and oxidation resistance of TiAlTaN coatings. Int J Refract Metals Hard Mater 2016;58:152-6.
59. Chen L, Holec D, Du Y, Mayrhofer PH. Influence of Zr on structure, mechanical and thermal properties of Ti-Al-N. Thin Solid Films 2011;519:5503-10.
60. Riedl H, Holec D, Rachbauer R, et al. Phase stability, mechanical properties and thermal stability of Y alloyed Ti-Al-N coatings. Surf Coat Technol 2013;235:174-80.
61. Xu YX, Chen L, Pei F, Du Y, Liu Y, Yue JL. Influence of Hf on the structure, thermal stability and oxidation resistance of Ti-Al-N coatings. Thin Solid Films 2014;565:25-31.
62. Mikula M, Plašienka D, Sangiovanni DG, et al. Toughness enhancement in highly NbN-alloyed Ti-Al-N hard coatings. Acta Mater 2016;121:59-67.
63. Zou HK, Chen L, Chang KK, Pei F, Du Y. Enhanced hardness and age-hardening of TiAlN coatings through Ru-addition. Scripta Mater 2019;162:382-6.
64. Hannah DC, Yang J, Podsiadlo P, et al. On the origin of photoluminescence in silicon nanocrystals: pressure-dependent structural and optical studies. Nano Lett 2012;12:4200-5.
65. Tang DM, Ren CL, Wang MS, et al. Mechanical properties of Si nanowires as revealed by in situ transmission electron microscopy and molecular dynamics simulations. Nano Lett 2012;12:1898-904.
66. Zhang Z, Cui J, Chang K, et al. Deformation induced new pathways in silicon. Nanoscale 2019;11:9862-8.
67. Wang B, Zhang Z, Chang K, et al. New deformation-induced nanostructure in silicon. Nano Lett 2018;18:4611-7.
68. Kamimura Y, Edagawa K, Iskandarov A, Osawa M, Umeno Y, Takeuchi S. Peierls stresses estimated via the Peierls-Nabarro model using ab-initio γ-surface and their comparison with experiments. Acta Mater 2018;148:355-62.
69. Leonardi AK, Ober CK. Polymer-based Marine antifouling and fouling release surfaces: strategies for synthesis and modification. Annu Rev Chem Biomol Eng 2019;10:241-64.
70. Verma J, Khanna AS, Sahney R, Bhattacharya A. Super protective anti-bacterial coating development with silica-titania nano core-shells. Nanoscale Adv 2020;2:4093-105.
71. Zhu Y, Dong M, Chang K, Li J, Wang L. Prolonged anti-bacterial action by sluggish release of Ag from TiSiN/Ag multilayer coating. J Alloys Compd 2019;783:164-72.
72. Zhu Y, Dong M, Zhao X, Li J, Chang K, Wang L. Self-healing of TiSiN/Ag coatings induced by Ag. J Am Ceram Soc 2019;102:7521-32.
73. Rajabi A, Ghazali M, Syarif J, Daud A. Development and application of tool wear: A review of the characterization of TiC-based cermets with different binders. Chem Eng J 2014;255:445-52.
74. Liu Y, Wang Z, Sun Q, et al. Tribological behavior and wear mechanism of pure WC at wide range temperature from 25 to 800 °C in vacuum and air environment. Int J Refract Metals Hard Mater 2018;71:160-6.
75. Sveen S, Andersson J, M’saoubi R, Olsson M. Scratch adhesion characteristics of PVD TiAlN deposited on high speed steel, cemented carbide and PCBN substrates. Wear 2013;308:133-41.
76. Emmerlich J, Music D, Braun M, Fayek P, Munnik F, Schneider JM. A proposal for an unusually stiff and moderately ductile hard coating material: Mo2BC. J Phys D: Appl Phys 2009;42:185406.
77. Xu YX, Chen L, Pei F, Chang KK, Du Y. Effect of the modulation ratio on the interface structure of TiAlN/TiN and TiAlN/ZrN multilayers: First-principles and experimental investigations. Acta Mater 2017;130:281-8.
78. Hintermann H. Advances and development in CVD technology. Mater Sci Eng A Struct Mater 1996;209:366-71.
79. Qiu L, Du Y, Wu L, et al. Microstructure, mechanical properties and cutting performances of TiSiCN super-hard nanocomposite coatings deposited using CVD method under the guidance of thermodynamic calculations. Surf Coat Technol 2019;378:124956.
80. Qiu L, Du Y, Wang S, et al. Mechanical properties and oxidation resistance of chemically vapor deposited TiSiN nanocomposite coating with thermodynamically designed compositions. Int J Refract Metals Hard Mater 2019;80:30-9.
81. Qiu L, Du Y, Wang S, et al. Through-process modeling and experimental verification of titanium carbonitride coating prepared by moderate temperature chemical vapor deposition. Surf Coat Technol 2019;359:278-88.
82. Sims CT, Stoloff NS, Hagel WC. Superalloys II: High-temperature materials for aerospace and industrial power. New York: Wiley; 1987.
83. Ruan J, Xu W, Yang T, et al. Accelerated design of novel W-free high-strength Co-base superalloys with extremely wide γ/γ′ region by machine learning and CALPHAD methods. Acta Mater 2020;186:425-33.
84. Nie H, Zhang T. Development of manufacturing technology on WC-Co hardmetals. Tungsten 2019;1:198-212.
85. Liu K, Wang Z, Yin Z, Cao L, Yuan J. Effect of Co content on microstructure and mechanical properties of ultrafine grained WC-Co cemented carbide sintered by spark plasma sintering. Ceram Int 2018;44:18711-8.
86. Huang S, Li L, Vanmeensel K, Van der Biest O, Vleugels J. VC, Cr3C2 and NbC doped WC-Co cemented carbides prepared by pulsed electric current sintering. Int J Refract Metals Hard Mater 2007;25:417-22.
87. Zhao C, Lu H, Liu X, Liu C, Nie Z, Song X. Strengthening cemented carbides by activated nano TaC. Int J Refract Metals Hard Mater 2021;95:105449.
88. Li N, Zhang W, Du Y, Xie W, Wen G, Wang S. A new approach to control the segregation of (Ta,W)C cubic phase in ultrafine WC-10Co-0.5Ta cemented carbides. Scripta Mater 2015;100:48-50.
89. Marquis EA, Hyde JM, Saxey DW, et al. Nuclear reactor materials at the atomic scale. Mater Today 2009;12:30-7.
90. Karoutas Z, Brown J, Atwood A, et al. The maturing of nuclear fuel: past to accident tolerant fuel. Prog Nucl Energy 2018;102:68-78.
91. Katoh Y, Snead LL, Szlufarska I, Weber WJ. Radiation effects in SiC for nuclear structural applications. Curr Opin Solid State Mater Sci 2012;16:143-52.
92. Nadeau JS. Very high pressure hot pressing of silicon carbide. Am Ceram Soc Bull 1973;52:170-4.
93. Liu M, Yang Y, Wei Y, et al. Preparation of dense and high-purity SiC ceramics by pressureless solid-state-sintering. Ceram Int 2019;45:19771-6.
94. Liu Y, Liu R, Liu M. Improved sintering ability of SiC ceramics from SiC@Al2O3 core-shell nanoparticles prepared by a slow precipitation method. Ceram Int 2019;45:8032-6.
95. Shao J, Li M, Chang K, et al. Fabrication and characterization of SPS sintered SiC-based ceramic from Y3Si2C2-coated SiC powders. J Eur Ceram Soc 2018;38:4833-41.
96. Xu K, Zou H, Chang K, et al. Thermodynamic description of the sintering aid system in silicon carbide ceramics with the addition of yttrium. J Eur Ceram Soc 2019;39:4510-9.
97. Gerdes MH, Witte AM, Jeitschko W, Lang A, Künnen B. Magnetic and electrical properties of a new series of rare earth silicide carbides with the compositionR3Si2C2(R=Y, La-Nd, Sm, Gd-Tm). J Solid State Chem 1998;138:201-6.
98. Xu K, Chen L, Chang K, et al. Thermodynamic description of the Dy-Si-C system in silicon carbide ceramics. Calphad 2020;68:101738.
99. Xu K, Chang K, Zhou X, et al. Thermodynamic descriptions of the light rare-earth elements in silicon carbide ceramics. J Am Ceram Soc 2020;103:3812-25.
100. Lipkina K, Hallatt D, Geiger E, et al. A study of the oxidation behaviour of FeCrAl-ODS in air and steam environments up to 1400 °C. J Nucl Mater 2020;541:152305.
101. Briggs SA, Edmondson PD, Littrell KC, et al. A combined APT and SANS investigation of α′ phase precipitation in neutron-irradiated model FeCrAl alloys. Acta Mater 2017;129:217-28.
102. Ejenstam J, Thuvander M, Olsson P, Rave F, Szakalos P. Microstructural stability of Fe-Cr-Al alloys at 450-550 °C. J Nucl Mater 2015;457:291-7.
103. Chang K, Meng F, Ge F, Zhao G, Du S, Huang F. Theory-guided bottom-up design of the FeCrAl alloys as accident tolerant fuel cladding materials. J Nucl Mater 2019;516:63-72.
104. Vilar R, Santos E, Ferreira P, Franco N, da Silva R. Structure of NiCrAlY coatings deposited on single-crystal alloy turbine blade material by laser cladding. Acta Mater 2009;57:5292-302.
105. Padture NP, Gell M, Jordan EH. Thermal barrier coatings for gas-turbine engine applications. Science 2002;296:280-4.
106. Pomeroy M. Coatings for gas turbine materials and long term stability issues. Mater Des 2005;26:223-31.
107. Fan L, Liu L, Yu Z, Cao M, Li Y, Wang F. Corrosion behavior of Ti60 alloy under a solid NaCl deposit in wet Oxygen flow at 600 °C. Sci Rep 2016;6:29019.
108. Shu Y, Wang F, Wu W. Corrosion behavior of pure Cr with a solid NaCl deposit in O2 plus water vapor. Oxid Met 2000;54:457-71.
109. Cao M, Liu L, Yu Z, Fan L, Ying L, Wang F. Studies on the corrosion behavior of Fe-20Cr alloy in NaCl solution spray at 600 °C. Corros Sci 2018;133:165-77.
110. Xu K, Chang K, Du Y, Wang L. Design of novel NiSiAlY alloys in marine salt-spray environment: Part I. Al-Si-Y and Ni-Si-Y subsystems. J Mater Sci Mater Med 2021;88:66-78.
111. Yu J, Guo S, Chen Y, et al. A two-stage predicting model for γ′ solvus temperature of L12-strengthened Co-base superalloys based on machine learning. Intermetallics 2019;110:106466.
112. Yu J, Wang C, Chen Y, Wang C, Liu X. Accelerated design of L12-strengthened Co-base superalloys based on machine learning of experimental data. Mater Des 2020;195:108996.
113. Rajan K. Materials informatics. Mater Today 2005;8:38-45.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Lou M, Xu K, Chen L, Hong C, Yuan Y, Du Y, Du Y, Chang K. Development of robust surfaces for harsh service environments from the perspective of phase formation and transformation. J Mater Inf 2021;1:5. http://dx.doi.org/10.20517/jmi.2021.02
AMA Style
Lou M, Xu K, Chen L, Hong C, Yuan Y, Du Y, Du Y, Chang K. Development of robust surfaces for harsh service environments from the perspective of phase formation and transformation. Journal of Materials Informatics. 2021; 1(1): 5. http://dx.doi.org/10.20517/jmi.2021.02
Chicago/Turabian Style
Lou, Ming, Kai Xu, Leilei Chen, Chengyuan Hong, Yuan Yuan, Yujie Du, Yong Du, Keke Chang. 2021. "Development of robust surfaces for harsh service environments from the perspective of phase formation and transformation" Journal of Materials Informatics. 1, no.1: 5. http://dx.doi.org/10.20517/jmi.2021.02
ACS Style
Lou, M.; Xu K.; Chen L.; Hong C.; Yuan Y.; Du Y.; Du Y.; Chang K. Development of robust surfaces for harsh service environments from the perspective of phase formation and transformation. J. Mater. Inf. 2021, 1, 5. http://dx.doi.org/10.20517/jmi.2021.02
About This Article
Copyright
Data & Comments
Data

 Cite This Article 62 clicks
Cite This Article 62 clicks




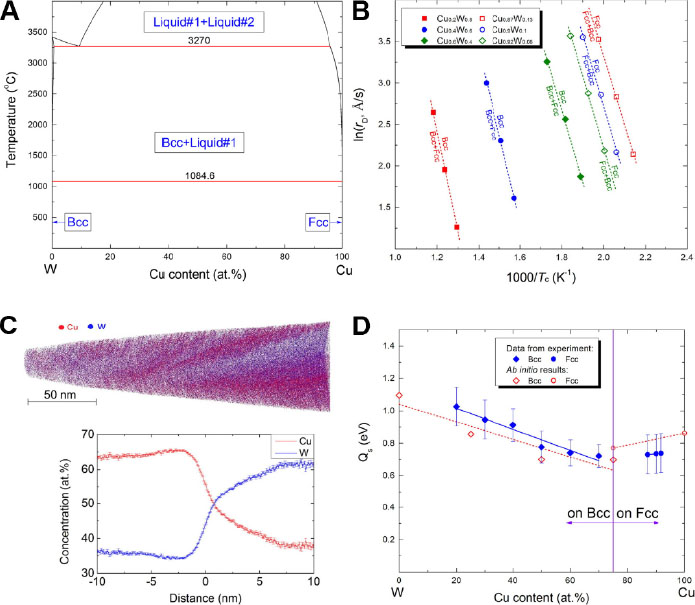
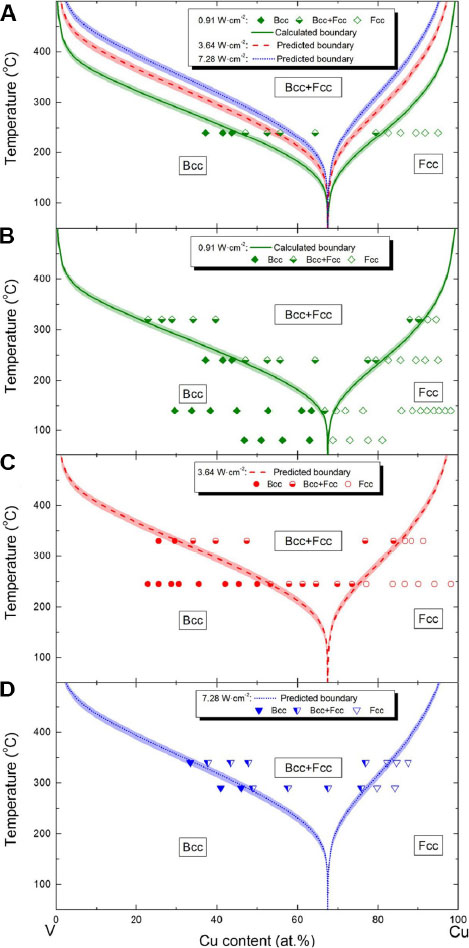




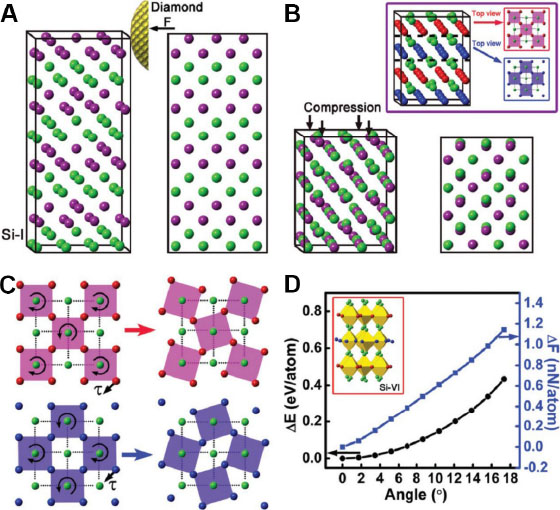
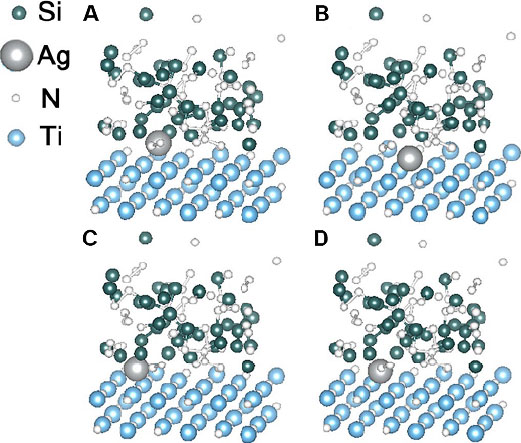

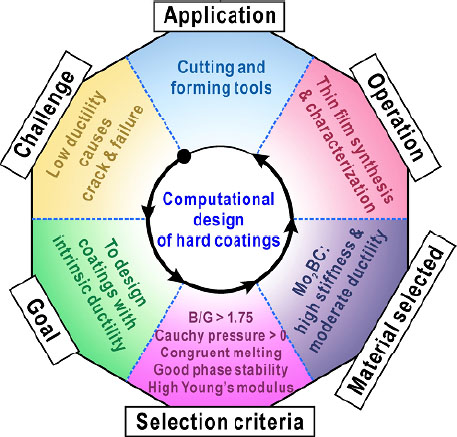
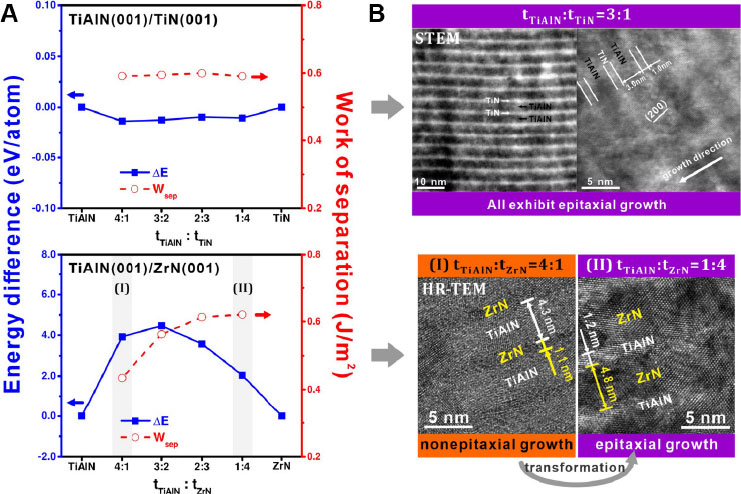
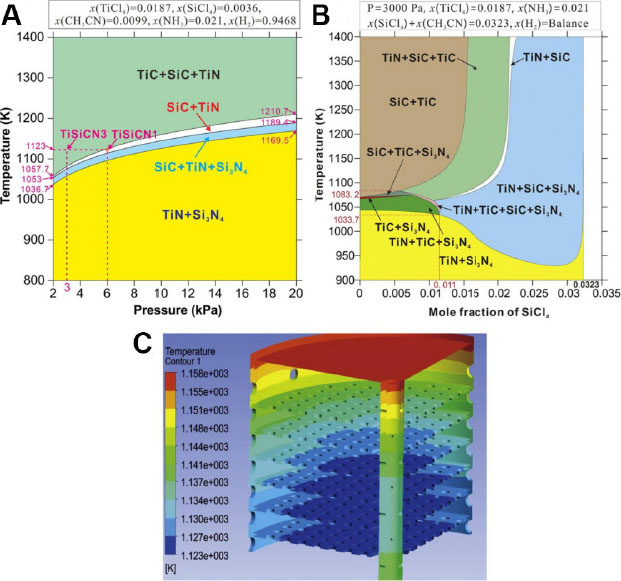
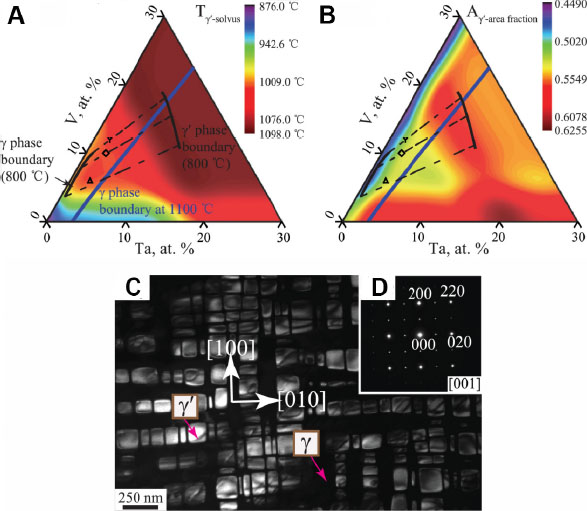

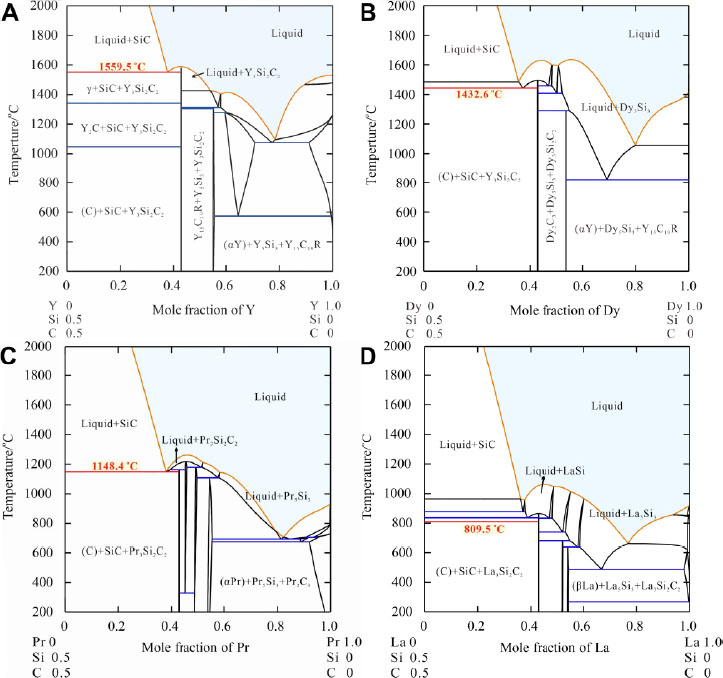
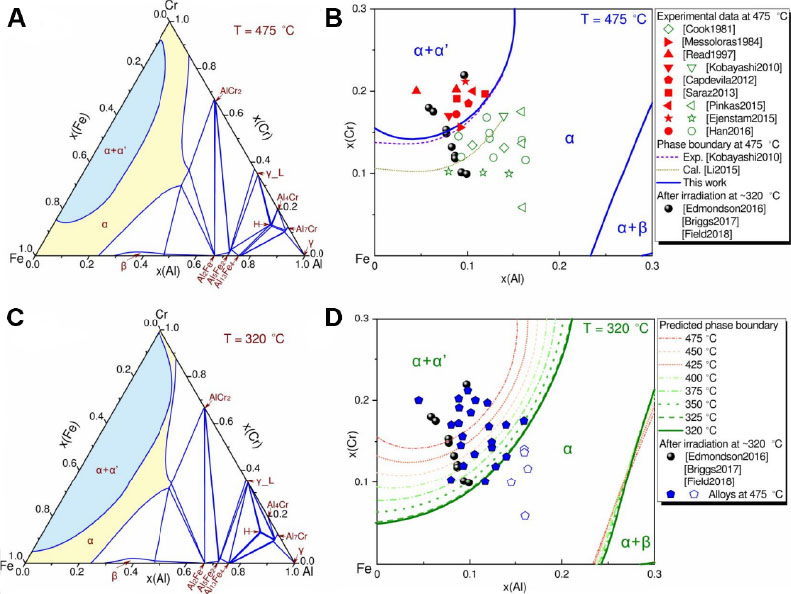
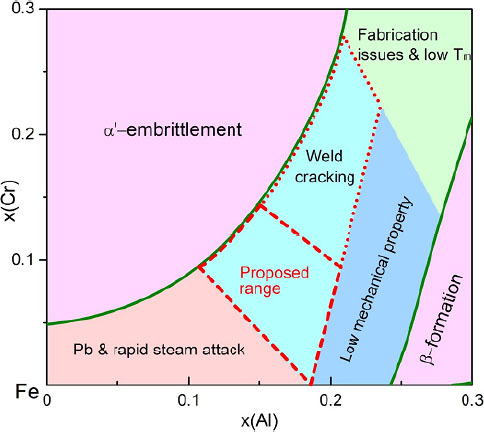
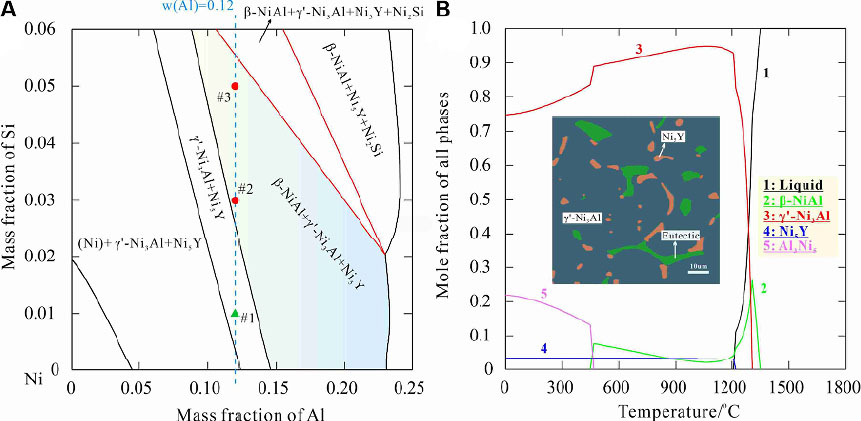










Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.