A metadata schema for lattice thermal conductivity from first-principles calculations
Abstract
Materials genome engineering databases represent fundamental infrastructures for data-driven materials design, in which the data resources should satisfy the FAIR (Findable, Accessible, Interoperable and Reusable) principles. However, a variety of challenges, such as data standardization, veracity and longevity, still impede the progress of data-driven materials science, including both high-throughput experiments and simulations. In this work, we propose a metadata schema for lattice thermal conductivity from first-principles calculations. The calculation workflow for lattice thermal conductivity includes structural optimization and the calculation of interatomic force constants and lattice thermal conductivity. The data generated during the calculation process corresponds to the virtual sample information, virtual source data and processed data, respectively, as specified in the General rule for materials genome engineering data of the Chinese Society for Testing and Materials. Following this general rule, the metadata structure and schema for each action are systematically defined and all metadata elements can be collected completely. Although this metadata schema is specific to lattice thermal conductivity calculations, it provides general rules and insights for other computational materials data in materials genome engineering.
Keywords
INTRODUCTION
To keep pace with the growing demands of materials science and industry, scientists and engineers hope to design novel functional materials on demand at low cost and within a short period. With great improvements in data generation efficiency by employing both high-throughput experimental and computational tools, there has been an explosion of materials databases. By combining these materials databases with data science and artificial intelligence, materials research has transformed from trial-and-error approaches to the data-driven paradigm[1-3]. Data-driven materials research has been considered as the fourth paradigm of materials research in addition to traditional theoretical, experimental and simulation approaches.
Benefiting from the various open or commercial materials simulation tools, computational materials science is experiencing vigorous development in the design of functional materials and the search for new materials by employing high-throughput screening and computation[4-7]. In particular, the calculation tools based on density functional theory (DFT) enable researchers working in materials science, physics and chemistry to understand the electronic structure of many-body systems, atoms, molecules and condensed phases[8,9]. In one DFT calculation, the data memory of the full inputs and outputs may exceed ten megabytes or even hundreds of megabytes. However, extremely small amounts of data subjectively collected from output files are generally presented in published figures or tables. Typically, the small subsets of data or results published in a research publication are directly relevant to the specific topic discussed in that publication, leading to most of the data produced by high-throughput approaches being stored in the local workstations of researchers. Moreover, publications only present basic calculation details, such as the type of code, exchange-correlation functional pseudopotential, plane-wave cutoff energy, k-mesh density and convergence criteria. The lack of full calculation details greatly prevents the achievement of exact duplication.
In recent years, various materials databases have been well developed. The Novel Materials Discovery (NOMAD) Repository[10] has been built to satisfy the increasing demand for storing and sharing materials science data. It offers the codes used in computational materials science and contains all the original inputs and outputs of data in the Materials Project database[11], Open Quantum Materials Database (OQMD)[12] and Automatic FLOW (AFLOW)[13]. However, the differences in terminology and representation inevitably lead to the data being heterogeneous and difficult for data analytics in data-driven modes[14]. As a result, the quality, consistency and comprehensiveness of data should be further improved to simplify data sharing, reduce the cost and increase the speed of the exchange of scientific information among researchers. Metadata provides information that helps establish relationships between data items and is defined by the National Information Standards Organization (NISO) as “the information we create, store and share to describe things, allows us to interact with these things to obtain the knowledge we need”. A metadata schema is a high-level document that establishes a common method for structuring and understanding data, and it includes the principles and implementation issues for utilizing the schema. Naturally, such metadata could be made into a standard when a consensus is reached in the professional community.
The FAIR (Findable, Accessible, Interoperable and Reusable) principles have been proposed to guide the optimal sharing and reuse of data[15] and therefore the guiding principles for scientific data. In general, a FAIR data infrastructure requires a detailed description of the approach to obtaining data, addressing metadata, ontologies and workflows[16]. However, only the researchers performing the experiments or calculations have the knowledge to provide detailed critical information.
At present, the microbiome metadata standards have been developed and reported successively by the microbiome research community to try to make the microbiome data truly FAIR[17]. However, in the field of medicine[18] and low-carbon energy research[19], although the data stakeholders are collaborative in advancing FAIR metadata schemas in their respective fields, there are challenges. Likewise, developing a metadata schema is essential in the widespread adoption of the data-driven model in materials science. However, materials science currently lacks such a model[20].
For a long time, materials data have faced a lack of unified management rules. The data from different sources vary significantly in content and format, resulting in unguaranteed data quality. Simultaneously, the data are not interoperable and data integration and analysis are extremely difficult. These challenges have created a non-negligible obstacle for the exertion of the cohesive effect of materials genome engineering data and the construction of data-driven ecological models. Standards organizations, such as the International Organization for Standardization [Available from: https://www.iso.org/home.html], have made attempts to provide control vocabularies and develop schemas for data formats and handing, but these have so far failed to reach wide adoption within the community[16]. The General rule for materials genome engineering data[21] (i.e., the General rule) of the Chinese Society for Testing and Materials (CSTM) is a pioneering attempt to standardize the content of data. In order to meet the requirements of data content and formatting in intelligent materials research and ensure the improvement of the quality and standardization of management for materials data, the proposed general rule standardizes the management method of materials data with FAIR principles to unlock the full potential of materials data.
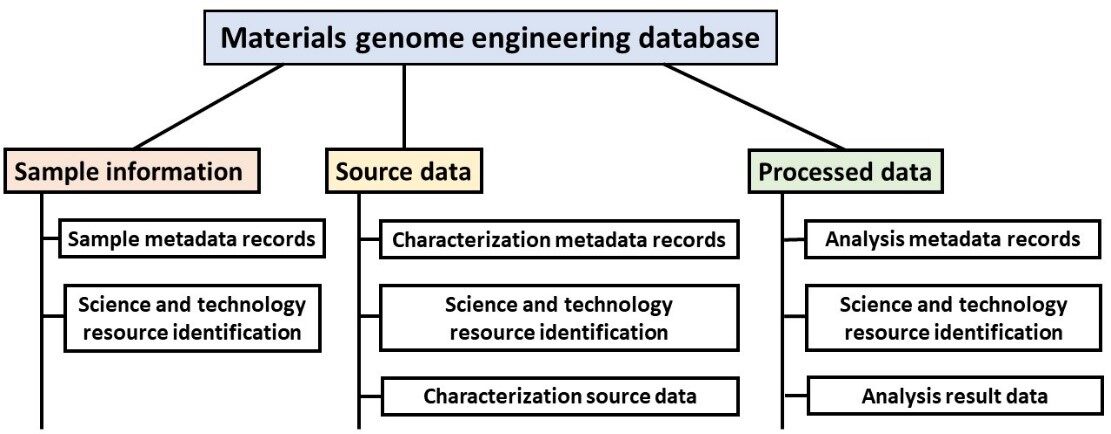
As shown in Figure 1, under the General rule, the data is generally divided into three classes: sample information (the material model generated by calculation is considered as the virtual sample); source data (the unprocessed materials data generated by characterization or measurement or virtual source data generated by calculation); processed data. Each data class includes independent resource identification, metadata records and results data. Each action event (sample preparation, sample characterization and data analysis) is defined as an individual entry unit that should collect the data related to the action as completely as possible. Therefore, the data standardized by the General rule can be easily findable, accessible and reusable. The General rule clarifies the basic content and standardization direction of materials genome engineering data from a macroscopic perspective. Since a clear and specific standardized process and implementation method have yet to be established, there are still great challenges in promoting the standardization of materials data. Metadata provides a comprehensive description of the content of the data, the process and context of its production, the method of access and acquisition and other characteristics. All these help data stakeholders find, access and utilize data faster and more rationally. The standardization of metadata will greatly promote the interoperability and integration of data. Very recently, the CSTM has proposed the Materials genome engineering data-Metadata standardization principle and method[22]. Under the guidance of the General rule, more specific experimental and computational metadata schemas need to be established as soon as possible.
Figure 1. Category and content of materials data following the General rule for materials genome engineering data[21].
Thermal conductivity is a fundamental transport property that indicates the thermal transport ability of a material. Heat in a solid is mainly carried by electrons and atomic variations. Electronic thermal conductivity (ke) is directly related to electrical conductivity (σ) via the Wiedemann-Franz law, ke = LσT, where L and T are the Lorentz number and temperature, respectively. In most semiconductors and insulators, atomic variations dominate thermal conductivity and in crystals are composed of normal modes, whose quanta are defined as phonons. Combining DFT and the phonon Boltzmann transport equation (PBTE) has enabled the calculation of lattice thermal conductivity with high precision and free of empirical parameters. Furthermore, DFT calculations provide detailed insights into phonon interaction events, thereby guiding the design of functional materials with ultrahigh or ultralow thermal conductivity[23,24].
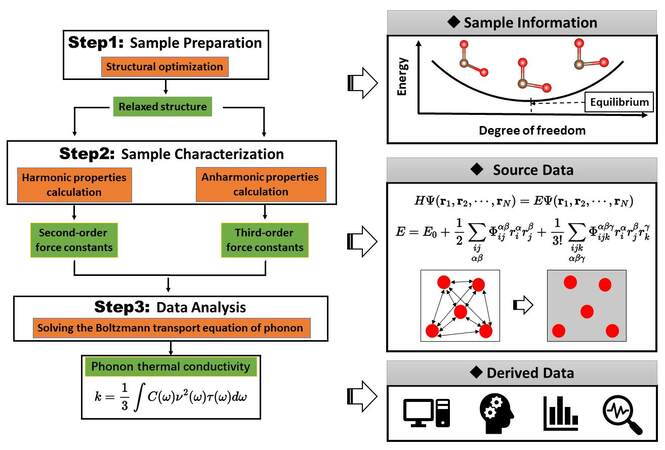
In this work, we propose a complete metadata schema for lattice thermal conductivity from first-principles calculations. From the top five DFT codes (Gaussian[25], VASP[26], QUANTUM ESPRESSO[27], CASTEP[28] and ORCA[29]) ranked by the number of citations [Available from: https://atomistic.software/#/table], VASP is taken as an example to conduct the detailed first-principles calculations. The second-order force constants (FC2) and third-order force constants (FC3) are calculated by employing VASP with the Phonopy[30] and Thirdorder[31] codes. Many packages, including ALAMODE[32], almaBTE[33], phono3py[34] and ShengBTE[35], can predict phonon thermal conductivity using force constants from DFT calculations. The open-source package, ShengBTE, is used to calculate the final lattice thermal conductivity based on the iterative solution to the PBTE in this work. Following the General rule, the overall workflow of the lattice thermal conductivity calculation is divided into three processes, namely, virtual sample preparation, virtual sample characterization and data analysis, as shown in Figure 2. The data generated during these processes correspond to the sample information, source data and processed data, respectively. The structural optimization is run via VASP to obtain the optimized crystal structure under a set of calculation parameter settings, including the pseudopotential, exchange-correction functional, electronic wave vector grid, plane-wave energy cutoff and energy and force convergence criteria. For the virtual sample characterization process, the fully optimized structure in step1 is taken as the input of step2 and the finite-difference supercell approach is conducted using the Phonopy and Thirdorder tools to obtain the FC2 and FC3 during the harmonic and anharmonic phonon property calculations, respectively. In the data analysis stem, the FC2 and FC3 calculated in step2 are then taken as inputs for solving the PBTE to obtain the final lattice thermal conductivity. The definitions of metadata structure and schema for each calculation step are presented in the following sections.
RESULTS AND DISCUSSION
Metadata schema for structural optimization
By solving the many-body Schrödinger equation or the Kohn-Sham equation, first-principles calculations enable us to understand the electronic structure of crystals and their derived physical or chemical properties at the atomic level. VASP is also employed to conduct ab initio quantum mechanical calculations using either Vanderbilt pseudo-potentials or the projector augmented wave (PAW) method and a plane-wave basis set. In general, structural optimization is the necessary and initial step for first-principles calculations to obtain a fully relaxed crystal structure under given convergence accuracy and a set of calculation parameters. It provides a relatively stable input structure for the subsequent calculations of crystal properties. Although the calculation parameter settings in different cases are subjective, the workflow and necessary files needed to run VASP are deterministic, thereby providing good conditions for the development of a metadata schema.
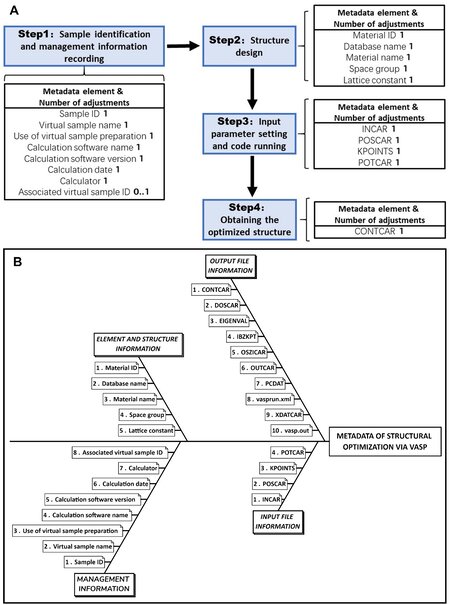
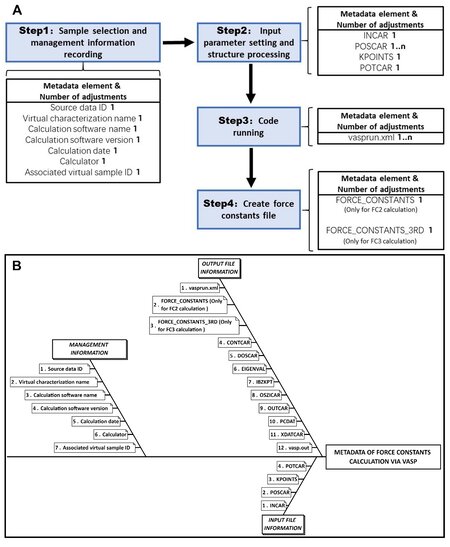
We formulate the basic framework of the metadata schema and summarize the necessary elements for structural optimization via VASP, as shown in Figure 3. The schema specifies a set of mandatory, conditional and optional metadata subsets, entities and elements. The metadata subset of structural optimization can be divided into four categories: management information; element and structure information; input file information; output file information. These are shown in Figure 3B and defined in detail as follows:
Figure 3. (A) Workflow for structural optimization. The metadata element and its number of adjustments in each step are listed. (B) Metadata structure for structural optimization.
MANAGEMENT INFORMATION specifies the basic information of the virtual sample preparation. The virtual sample is assigned with an independent resource identification (ID) and the employed calculation method, calculator, date and purpose should be recorded simultaneously.
ELEMENT AND STRUCTURE INFORMATION contains the specifics of the crystal structure of the material. The unique ID of the calculation object in materials databases must be provided, which makes it easy to determine the full element information and the geometric structure of the material. Furthermore, general information, including the material”s name, space group number and lattice constants, is also included in this part.
INPUT FILE INFORMATION contains four necessary input files to run VASP. The INCAR is the central input file of VASP, which determines what to do and how to do the calculation. The INCAR tags specified in the file select the detail algorithms and set the calculation parameters. The KPOINTS file specifies the Blöch vector used to mesh the Brillouin zone. The POSCAR contains the lattice geometry and ionic positions. The POTCAR essentially contains the pseudopotential for each atomic species used in the calculation.
OUTPUT FILE INFORMATION contains the output file of the fully relaxed crystal structure. The CONTCAR has the same format as the POSCAR and can be used for the next round of calculations. All output files from VASP calculations are listed.
The computational workflow, as well as the metadata elements, is shown in Figure 3A, which consists of four steps: (i) assigning the ID of the virtual sample and recording the calculation information; (ii) selecting the crystal structure; (iii) preparing the four input files for the parallel computation; (iv) running VASP and obtaining the fully optimized structure under specific convergence accuracy. The number of adjustments for all metadata elements is set to be one except for the associated virtual sample ID, which is given if the calculation is the continuation of the previous sample preparation process and is therefore a conditional element.
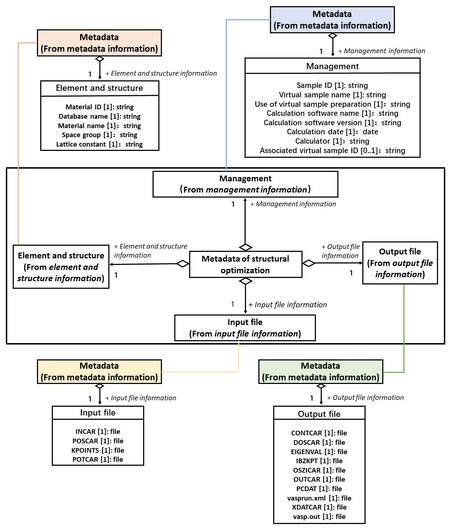
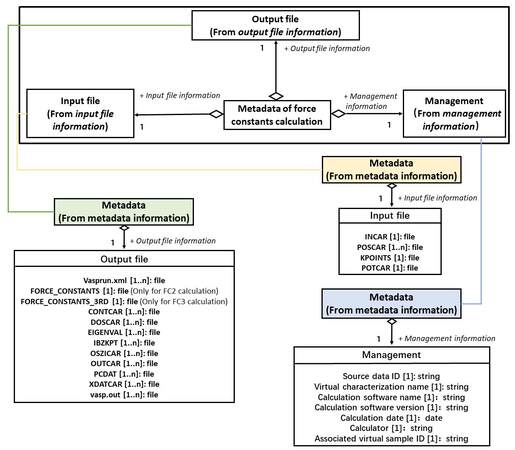
Each metadata subset is individual and contains the complete metadata element. The relationship between metadata subset, entity and element is constructed by the Unified Modeling Language (UML), a general-purpose and developmental modeling language in the field of software engineering that is intended to provide a standard method to visualize the design of a system. As shown in Figure 4, the four individual metadata entities corresponding to the four metadata subsets in Figure 3B are logically connected with the parent class using an aggregation method. The parent class “Metadata of structural optimization” comprises four unique child classes “Management, Element and structure, Input file and Output file”. Here, each child class plays a different role in the integrity of the parent class. The UML schema indicating the relationship between metadata entity and element is also built up similarly. Taking the metadata entity “Input file” as an example, the parent class “Metadata of structural optimization” contains only one child class whose name is “Input file” and the “Input file information” connects the relationship between child class and parent class. The four input files “INCAR, POSCAR, KPOINTS and POTCAR” for the VASP calculation are treated as metadata elements to be aggregated into the “Input file” class. Moreover, the maximum number of occurrences and the type of metadata elements are also indicated in the UML diagram.
Figure 4. Metadata schema of structural optimization constructed by UML. UML: Unified Modeling Language.
The metadata schema defines the description convention from both semantics and syntax. The six attributes, namely, Name, Definition, Data type, Range, Restriction and Maximum number of occurrences, are given in the data dictionary in Supplementary Table 1, which provides a full description of these attributes of metadata entities and elements in structural optimization via VASP. On this basis, the metadata collected from the virtual sample preparation process using VASP are standardized in a scientific style.
Metadata schema for calculation of force constants
After obtaining the relatively stable crystal structure, we then move to the calculation of the force constants. FC2 and FC3 are the second- and third-order derivatives of the potential energy, respectively, which can be written as Taylor expansions of displacements with respect to the equilibrium potential. FC2 is used to perform lattice dynamics to derive the harmonic phonon properties, including phonon dispersions, group velocity v(ω) and specific heat C(ω). FC3 is used to compute the anharmonic relaxation time τ(ω) based on Fermi’s golden rule. The force constants are the bridge to connect the crystal structure of a material with its lattice thermal conductivity. Due to the similarity of the calculation process for FC2 and FC3, only one metadata schema is defined for the two types of force constants. Recently, fourth-order force constants have been used to compute τ(ω) and then derive the lattice thermal conductivity with the consideration of high-order phonon interactions. For the proposed metadata schema in this work, although we only consider the third-order FC3 and three-phonon scattering process, the higher-order force constants or phonon scattering processes can be easily extended.
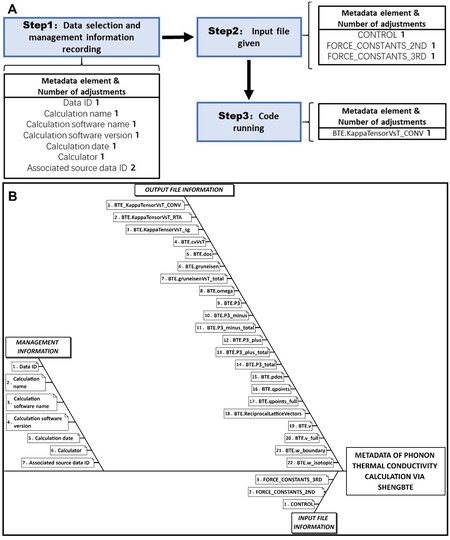
For the metadata schema of force constant calculations via VASP, we formulate the workflow in Figure 5A and show the logical relationship between metadata entities and elements in Figure 5B. The metadata subsets of force constants are divided into three categories: management information; input file information; output file information. These are defined as follows:
Figure 5. (A) Workflow of force constant calculation. The metadata element and its number of adjustments in each step are listed. (B) Metadata structure of force constant calculation.
MANAGEMENT INFORMATION specifies the basic information for virtual sample characterization. The individual characterization process is assigned with an independent resource ID. The calculation name, method, calculator and date should be recorded simultaneously. The characterization process is a continued action after the sample preparation process. Thus, the associated virtual sample ID should be given here.
INPUT FILE INFORMATION contains the four necessary input files for a successful VASP run. In the INCAR, the finite-difference method is employed for computing force constants, so the parameter settings should follow the static self-consistency principle in VASP. In the KPOINTS, the k-mesh density could be appropriately decreased compared with that in structural optimization because of the supercell method we use to compute force constants. For the POSCAR, in the pre-process, supercell structures with displacements are created from a unit cell by Phonopy or third order. The POSCAR contains the supercell structural information with displacements. In the POTCAR, the type of pseudopotential is the same as that used in structural optimization.
OUTPUT FILE INFORMATION contains the output file for interatomic force analysis. vasprun.xml is the output file in XML format after a successful VASP job, which can be used for quick analysis of the electronic band structure, interatomic forces, dynamic matrix, dielectric constants, and so on. In the FORCE_CONSTANTS, the second-order interatomic force constant matrix is built by Phonopy. FORCE_CONSTANTS_3RD contains the third-order interatomic force constant matrix built by Thirdorder. All output files from the VASP calculations are listed.
The computational workflow of the force constant calculation is shown in Figure 5A. Firstly, we choose the optimized structure and appropriate tool for the supercell calculation and assign the ID for the data relevant to force constants. The other management information should also be recorded. Secondly, we determine the standard input files for the VASP calculation. Phonopy and Thirdorder are separately used to generate two sets of displaced supercell configurations with consideration of the supercell size and cutoff radius. Thirdly, the interatomic forces of the displaced supercell structures are computed. Finally, Phonopy and Thirdorder gather the interatomic forces to build the FC2 and FC3 matrixes, respectively.
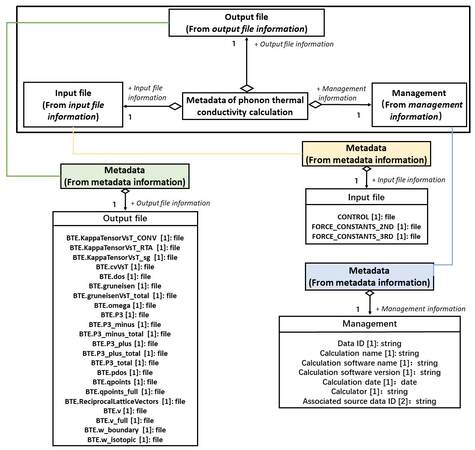
The metadata schema of the force constant calculation is shown in Figure 6. The parent class “Metadata of force constants calculation” consists of three child classes, namely, Management, Input file and Output file. The metadata elements in each metadata entity are also listed, indicating the maximum number of occurrences and types. Similarly, the complete metadata with attribute identification is listed in
Metadata schema for calculation of lattice thermal conductivity
The energy and force information obtained from first-principles calculations enable us to further analyze the crystal properties. In general, users pay more attention to the data obtained by analyzing and processing the existing source data. In the framework of thermal conductivity calculations discussed herein, the PBTE is iteratively solved using ShengBTE, which takes FC2 and FC3 as inputs.
In the metadata schema, the organized metadata structure for the lattice thermal conductivity calculation shown in Figure 7B is divided into three modules, namely, management information, input file information and output file information. These are defined as follows:
Figure 7. (A) Workflow of lattice thermal conductivity calculation. The metadata element and its number of adjustments in each step are listed. (B) Metadata structure of lattice thermal conductivity calculation.
MANAGEMENT INFORMATION specifies the basic information of the data analysis. It contains the ID assigned to the derived data, calculation name, method, calculator and date. Since the thermal conductivity calculation is a continuous action after the step2 (shown in Figure 2), the source data ID indicating the source of force constants should be given.
INPUT FILE INFORMATION contains the three essential input files for the successful run of ShengBTE software. The contents of the CONTROL file describe the system to be studied and specify a set of parameters and flags controlling execution. FORCE_CONSTANRS_2ND and FORCE_CONSTANR_3RD correspond to FC2 and FC3, respectively.
OUTPUT FILE INFORMATION contains BTE.KappaTensorVsT_CONV, which gives the total converged thermal conductivity tensor in units of W/(m K) as a function of temperature. All output files from the ShengBTE calculations are listed and a detailed description of the output files is shown in the manual for ShengBTE [Available from: https://www.shengbte.org/documentation].
Figure 7A shows the general workflow of the lattice thermal conductivity calculation with the corresponding metadata element in each step. Furthermore, the metadata schema of the lattice thermal conductivity calculation is displayed in Figure 8 and three different types of metadata are collected. In particular, since FC2 and FC3 are obtained from two individual virtual sample characterization processes, the number of occurrences for the associated data ID is set to two. All the collected metadata in the lattice thermal conductivity calculation is shown in the data dictionary in Supplementary Table 3. The metadata structure and schema are similar to that of the first two metadata schemas.
Example
Under the guidance of the proposed metadata schema, we take the well-studied silicon as an example. Three metadata example tables with respect to structural optimization, second and third force constant calculation and lattice thermal conductivity calculation are presented in Supplementary Tables 4-6, respectively. Furthermore, all input and output files in the three calculation processes are also attached in the Supplementary Data. We plot the calculated lattice thermal conductivity of Si as a function of temperature in Figure 9. In general, the calculated lattice thermal conductivity agrees reasonably well with the experimental and theoretical data. For example, at 900 K, the calculated lattice thermal conductivity is 41 W/(m K), in good agreement with the reported result [43 W/(m K)][36]. At 300 K, the calculated value is 131 W/(m K), a little smaller than 146 W/(m K)[37] and 140 W/(m K)[38] due to the sparse q-mesh in our calculation. Except for the commercial software VASP, the metadata schema for lattice thermal conductivity calculation with open-source QUANTUM ESPRESSO software is proposed. Due to the similarity of the workflow for lattice thermal conductivity calculations between the two electronic-structure codes, only the metadata example tables [Supplementary Tables 6-8] of Si computed by QUANTUM ESPRESSO are added to the Supplementary Materials. The input and output files in QUANTUM ESPRESSO are also attached in the Supplementary Data.
CONCLUSIONS AND PERSPECTIVES
The cornerstone of data-driven materials research is to have datasets consisting of a massive number of AI-ready data suitable for the utilization of artificial intelligence techniques. The standardization of data is a key part of ensuring data quality. The General rule[21] is a pioneering effort to provide a basic regulation to the content of data, which specifies that the materials data are generally divided into three classes: sample information (the material model generated by calculation is considered the virtual sample); source data (the unprocessed material data generated by the characterization or measurement or virtual source data generated by calculation); processed data. Each individual data entry should cover only one action event (sample preparation, sample characterization or data analysis) and collect the information related to the action as completely as possible.
Motivated by the urgent demands in materials science and the community for sharing and exchanging data, we have proposed a full metadata schema for lattice thermal conductivity from first-principles calculations. The calculation of lattice thermal conductivity is divided into three consecutive processes, namely, structural optimization, force constant calculation and lattice thermal conductivity calculation. The data generated during the three processes now directly corresponds to the virtual sample information, virtual source data and derived data, respectively, as specified in the General rule for materials genome engineering data. For each process and type of data, a detailed metadata schema has been proposed with grouped metadata element sets. Moreover, the schemas are constructed to logically connect the metadata entities with metadata elements. The proposed metadata schema for lattice thermal conductivity in this work should give useful insights for the other computational materials data.
This study provides an exemplary use case when applying the General rule to the first-principles calculations of lattice thermal conductivity. This methodology is certainly extendable when generating a set of metadata schemas for all the other data generated by first-principles calculation. The templates for the data of the virtual sample, the directly calculated parameters and the intended final results can be easily adapted into schemas of other circumstances of first-principles calculations through proper alternation. The metadata schema for structural optimization can also be used for the framework in electron transport beyond lattice thermal conductivity. Furthermore, all the calculation details, including the sample, management and calculation information, have been recorded in our proposed metadata schema for structural optimization, which makes the generated data reusable in other first-principle calculations. Simultaneously, since this set of schema is designed specifically for the first-principles calculations of lattice thermal conductivity, it is not directly adoptable to the applications of other categories of calculations. For those calculations operating under totally different frameworks, such as molecular dynamics simulations and CALPHAD, new model metadata schemas need to be developed separately.
The metadata and the metadata schema we proposed are free for usage. Attentionally, the proposition of metadata schema aims to accelerate the data generated from computational and experimental tools to be in line with the FAIR rules and greatly promote the interoperability and integration of data. Certainly, the commercial computation codes used to generate data in the proposed metadata schema should be with a license.
DECLARATIONS
Authors’ contributionsPerformed the research and drafted the manuscript: Rao Y
Designed the study, performed data analysis and interpretation, revised, and finalized the manuscript: Rao Y, Lu Y, Zhang L, Ju S, Yu N, Zhang A, Chen L, Wang H
Availability of data and materialsThe data dictionary and metadata example table can be seen in Supplementary Materials, and all input and output files of Si calculation are attached in Supplementary Data. The Extensible Markup Language schema of the proposed metadata schema is available from https://github.com/SJTU-MI/kappa-metadata-schema.
Financial support and sponsorshipThis work was supported by the National Key R&D Program of China (2021YFB3702300), National Natural Science Foundation of China (No. 52006134), and Shanghai Pujiang Program (No. 20PJ1407500), and the Major Science and Technology Project of Yunnan Province “Genome Engineering of Rare and Precious Metal Materials in Yunnan Province (Phase One 2020)” (No. 202002AB080001-1). The computations in this paper were run on the π 2.0 cluster supported by the Center for High Performance Computing at Shanghai Jiao Tong University.
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2022.
Supplementary MaterialsREFERENCES
1. Schleder GR, Padilha ACM, Acosta CM, Costa M, Fazzio A. From DFT to machine learning: recent approaches to materials science-a review. J Phys Mater 2019;2:032001.
2. Agrawal A, Choudhary A. Perspective: materials informatics and big data: realization of the “fourth paradigm” of science in materials science. APL Mater 2016;4:053208.
3. Wang H, Xiang X, Zhang L. On the data-driven materials innovation infrastructure. Engineering 2020;6:609-11.
4. Jain A, Hautier G, Moore CJ, et al. A high-throughput infrastructure for density functional theory calculations. Comput Mater Sci 2011;50:2295-310.
5. Curtarolo S, Hart GL, Nardelli MB, Mingo N, Sanvito S, Levy O. The high-throughput highway to computational materials design. Nat Mater 2013;12:191-201.
6. Castelli IE, Olsen T, Datta S, et al. Computational screening of perovskite metal oxides for optimal solar light capture. Energy Environ Sci 2012;5:5814-9.
7. Potyrailo R, Rajan K, Stoewe K, Takeuchi I, Chisholm B, Lam H. Combinatorial and high-throughput screening of materials libraries: review of state of the art. ACS Comb Sci 2011;13:579-633.
8. Kohanoff J, Gidopoulos N I. Density functional theory: basics, new trends and applications. handbook of molecular physics and quantum chemistry 2003;2:532-568. Available from: https://bbs.sciencenet.cn/blog/admin/images/upfiles/20071017221454599631.pdf [Last accessed on 27 Oct 2022].
9. Johnson BG, Gill PMW, Pople JA. The performance of a family of density functional methods. J Chem Phys 1993;98:5612-26.
10. Ghiringhelli LM, Carbogno C, Levchenko S, et al. Towards efficient data exchange and sharing for big-data driven materials science: metadata and data formats. npj Comput Mater 2017:3.
11. Jain A, Ong SP, Hautier G, et al. Commentary: the materials project: a materials genome approach to accelerating materials innovation. APL Materials 2013;1:011002.
12. Kirklin S, Saal JE, Meredig B, et al. The open quantum materials database (OQMD): assessing the accuracy of DFT formation energies. npj Comput Mater 2015:1.
13. Curtarolo S, Setyawan W, Hart GL, et al. AFLOW: an automatic framework for high-throughput materials discovery. Comput Mater Sci 2012;58:218-26.
14. Rajan K. Materials informatics: the materials “gene” and big data. Annu Rev Mater Res 2015;45:153-69.
15. Wilkinson MD, Dumontier M, Aalbersberg IJ, et al. The FAIR guiding principles for scientific data management and stewardship. Sci Data 2016;3:160018.
16. Scheffler M, Aeschlimann M, Albrecht M, et al. FAIR data enabling new horizons for materials research. Nature 2022;604:635-42.
17. Vangay P, Burgin J, Johnston A, et al. Microbiome metadata standards: report of the national microbiome data collaborative’s workshop and follow-on activities. mSystems 2021;6:e01194-20.
18. Gennari JH, König M, Misirli G, Neal ML, Nickerson DP, Waltemath D. OMEX metadata specification (version 1.2). J Integr Bioinform 2021:18.
19. Wierling A, Schwanitz VJ, Altinci S, et al. FAIR metadata standards for low carbon energy research - a review of practices and how to advance. Energies 2021;14:6692.
20. Coudert F. Materials databases: the need for open, interoperable databases with standardized data and rich metadata. Adv Theory Simul 2019;2:1900131.
21. Chinese Society for Testing and Materials (CSTM). T/CSTM 00120-2019: General rule for materials genome engineering data. Available from: http://www.cstm.com.cn/article/details/ef49a444-80ca-4e71-99eb-e1e76c039d9f [Last accessed on 27 Oct 2022].
22. Chinese Society for Testing and Materials (CSTM). T/CSTM 00837-2022: materials genome engineering data-Metadata standardization principle and method. Available from: http://www.cstm.com.cn/article/details/390ce11f-41a2-4d01-8544-04012bb13782 [Last accessed on 27 Oct 2022].
23. Ju S, Yoshida R, Liu C, et al. Exploring diamondlike lattice thermal conductivity crystals via feature-based transfer learning. Phys Rev Materials 2021:5.
24. Ju S, Shiomi J. Materials informatics for heat transfer: recent progresses and perspectives. Nanoscale Microscale Thermophys Eng 2019;23:157-72.
25. Frisch M J, Trucks G W, Schlegel H B, et al. Gaussian 16, revision C.01. Available from: https://gaussian.com/ [Last accessed on 27 Oct 2022].
26. Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B Condens Matter 1996;54:11169-86.
27. Giannozzi P, Baroni S, Bonini N, et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J Phys Condens Matter 2009;21:395502.
28. Pickard CJ, Mauri F. All-electron magnetic response with pseudopotentials: NMR chemical shifts. Phys Rev B 2001:63.
30. Chaput L, Togo A, Tanaka I, Hug G. Phonon-phonon interactions in transition metals. Phys Rev B 2011:84.
31. Li W, Lindsay L, Broido DA, Stewart DA, Mingo N. Thermal conductivity of bulk and nanowire Mg2SixSn1-x alloys from first principles. Phys Rev B 2012:86.
32. Tadano T, Gohda Y, Tsuneyuki S. Anharmonic force constants extracted from first-principles molecular dynamics: applications to heat transfer simulations. J Phys Condens Matter 2014;26:225402.
33. Carrete J, Vermeersch B, Katre A, et al. almaBTE : A solver of the space-time dependent Boltzmann transport equation for phonons in structured materials. Comp Phys Commun 2017;220:351-62.
34. Togo A, Chaput L, Tanaka I. Distributions of phonon lifetimes in Brillouin zones. Phys Rev B 2015:91.
35. Li W, Carrete J, A. Katcho N, Mingo N. ShengBTE: a solver of the Boltzmann transport equation for phonons. Comp Phys Commun 2014;185:1747-58.
36. Gu X, Li S, Bao H. Thermal conductivity of silicon at elevated temperature: role of four-phonon scattering and electronic heat conduction. Int J Heat Mass Transfer 2020;160:120165.
37. Liao B, Qiu B, Zhou J, Huberman S, Esfarjani K, Chen G. Significant reduction of lattice thermal conductivity by the electron-phonon interaction in silicon with high carrier concentrations: a first-principles study. Phys Rev Lett 2015;114:115901.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Rao Y, Lu Y, Zhang L, Ju S, Yu N, Zhang A, Chen L, Wang H. A metadata schema for lattice thermal conductivity from first-principles calculations. J Mater Inf 2022;2:17. http://dx.doi.org/10.20517/jmi.2022.20
AMA Style
Rao Y, Lu Y, Zhang L, Ju S, Yu N, Zhang A, Chen L, Wang H. A metadata schema for lattice thermal conductivity from first-principles calculations. Journal of Materials Informatics. 2022; 2(4): 17. http://dx.doi.org/10.20517/jmi.2022.20
Chicago/Turabian Style
Rao, Yongchao, Yongchao Lu, Lanting Zhang, Shenghong Ju, Ning Yu, Aimin Zhang, Li Chen, Hong Wang. 2022. "A metadata schema for lattice thermal conductivity from first-principles calculations" Journal of Materials Informatics. 2, no.4: 17. http://dx.doi.org/10.20517/jmi.2022.20
ACS Style
Rao, Y.; Lu Y.; Zhang L.; Ju S.; Yu N.; Zhang A.; Chen L.; Wang H. A metadata schema for lattice thermal conductivity from first-principles calculations. J. Mater. Inf. 2022, 2, 17. http://dx.doi.org/10.20517/jmi.2022.20
About This Article
Copyright
Data & Comments
Data

 Cite This Article 23 clicks
Cite This Article 23 clicks













Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.