A thermodynamic database of the Ni-Mo-Re system
Abstract
Thermodynamic databases are essential prerequisites for developing advanced materials, such as Ni-based superalloys. The present work collects a large amount of experimental and first-principles calculation data concerning the thermodynamics and phase diagrams of the Ni-Mo-Re system, based on which the thermodynamic properties of the ternary and its binary sub-systems Ni-Mo and Mo-Re are assessed by means of the CALculation of PHAse Diagrams (CALPHAD) approach. The thermodynamic database containing all model parameters is established and most experimental data are reproduced satisfactorily. The present work demonstrates the use of the CALPHAD method as a practical appliance in the toolbox of materials informatics to analyze and discriminate various types of data by thermodynamic modeling and then produce more useful data in wider ranges of compositions and temperatures by computational predictions.
Keywords
INTRODUCTION
Ni-based superalloys play a significant role in high-temperature applications for modern industry[1]. Refractory alloying elements, such as Mo and Re, are often added to enhance the high-temperature performance of Ni-based superalloys further. However, some harmful brittle topologically close-packed (TCP) phases may form with increasing contents of alloying elements. In order to understand the phase stabilities of TCP phases, as well as their equilibria with other phases, it is necessary to develop a reliable thermodynamic database to predict phase equilibria and transformations in Ni-based superalloys, starting from ternaries, such as Ni-Mo-Re.
The phase diagram and thermodynamics of the Ni-Mo-Re ternary system were studied by Yaqoob and Joubert[2,3] and the enthalpies of formation of compounds were calculated by Crivello[4] by means of first-principles calculations. A new phase with a modulated
The present work aims to obtain a set of self-consistent thermodynamic parameters of the Ni-Mo-Re system with more inputs from first-principles calculations. The binary systems Ni-Mo and Mo-Re are revised to obtain a better agreement with the experimental data. By combining the thermodynamic description of the Ni-Re system reported by Yaqoob and Joubert[6] with the updated Ni-Mo and Mo-Re systems, the reassessment of the Ni-Mo-Re ternary system is carried out.
LITERATURE REVIEW
All available experimental studies[3,7-46] are summarized in Table 1.
Performance accuracy (%) with patch images
| Type of data | Reference | Method | Quoted mode | |
| TA: Thermal analysis; OM: optical metallography; XRD: X-ray diffraction; CA: chemical analysis; DTA: differential thermal analysis; DC: diffusion couple; EPMA: electron probe microanalysis; EPS: electrolytic phase separation; EA: equilibrated alloys; DM: diffusion multiple; AC: adiabatic calorimetry; EMF: electromotive force; FP: first-principles calculations; VSM: vibrating sample magnetometer; SQUID: superconducting quantum interference device. aIndicates whether the data are used or not in the assessment: | ||||
| Ni-Mo binary system | ||||
| Phase equilibria | 70-85 at.% Ni | Grube et al.[7] | ▎ | |
| 60-76 at.% Ni | Bloom et al.[8] | |||
| fcc | Guthrie et al.[9] | |||
| Overall | Casselton et al.[10] | TA, OM, XRD | ||
| bcc liquidus | Wicker et al.[11] | CA, DTA | ||
| Below 1600 K | Heijwegen et al.[12] | DC, EPMA | ||
| fcc | Gust et al.[13] | (Not available) | ||
| bcc solidus | Kang et al.[14] | EPS, EPMA | ||
| fcc + Ni4Mo | Kobayashi et al.[15] | XRD | ||
| bcc solidus, fcc + | Yaqoob et al.[3] | EA, EPMA | ||
| 1173K and 1073K | Zhu et al.[16] | DM, EPMA | ||
| 1373K and 1123K | Shi et al.[17] | DC, EA, SEM, XRD | ||
| Thermodynamic properties | Enthalpy of mixing of liquid | Chistyakov et al.[18] | Calorimetry | |
| Sudavtsova[19] | Calorimetry | ▎ | ||
| Enthalpy of formation for | Spencer et al.[20] | AC | ||
| Enthalpies of formation for | Kubaschewski et al. [21] | AC | ||
| Heat capacity of Ni | Norem[22] | AC | ||
| Brook et al.[23] | AC | ▎ | ||
| Basak[24] | AC | |||
| Activity | Katayama et al.[25] | EMF | ▎ | |
| Meshkov et al.[26] | EMF | |||
| Tsai et al.[27] | EMF | |||
| Pejryd[28,29] | EMF | ▎ | ||
| Koyama et al.[30] | EMF | |||
| Sudavtsova[19] | EMF | ▎ | ||
| Curie temperature | Khan et al.[34] | VSM, SQUID | ||
| Magnetic moment | Ghosh et al.[35] | VSM, SQUID | ||
| Mo-Re system | ||||
| Phase equilibria | Overall | Dickinson et al.[36] | OM, XRD | |
| Knapton et al.[37] | OM, XRD | |||
| Savitskii et al.[38,39] | OM, XRD | |||
| Thermodynamic properties | 1473K and 1873K, enthalpy of formation | Farzadfar et al.[40] | OM, XRD, DRC | |
| Ni-Mo-Re system | ||||
| Phase equilibria | 1425K | Kodentsov et al.[41] | DC | ▎ |
| 1425K | Borisov et al. [42] Slyusarenko et al. [43] | DC & EA | ||
| 1473K | Feng et al.[44] | DM | ▎ | |
| 1473K and 1873K, liquidus projection | Yaqoob et al.[3] | EA, EPMA, XRD | ||
| Thermodynamic properties | Site occupancy of | Yaqoob et al.[45] | XRD | |
| Heat capacity of NMR-75 | Chekhovskoi et al.[45] | AC | ▎ | |
Ni-Mo
The Ni-Mo system has been extensively investigated by experiments[3,7-33] and thermodynamic modeling[32,33,47-49]. Due to the lack of experimental and first-principles calculated thermodynamic data, earlier thermodynamic assessments[47,48] are less reliable considering the formation enthalpies of some intermetallic compounds. Morishita et al. treated the
Mo-Re
Thermodynamic assessments of the Mo-Re system have been published by many authors[50-53]. Mathieu et al. reviewed all the previous work and performed reassessments aided by first-principles calculations[53]. A full five-sublattice (5SL) model and various simplified sublattice models of the
Ni-Re
The experimental information of the Ni-Re binary system before 1985 has been reviewed critically by Nash et al. and an assessed Ni-Re phase diagram was reported[54]. Later, Yaqoob and Joubert reinvestigated experimentally and reassessed this binary system, and agreed well with most experimental data[6]. Furthermore, the invariant reaction temperature and corresponding compositions determined by Yaqoob and Joubert[6] were reconfirmed by Boettinger et al.[55]. Thus, the thermodynamic parameters from Yaqoob and Joubert[6] were directly employed in the present work.
Ni-Mo-Re
Several experimental investigations have been carried out on the phase equilibria of the Ni-Mo-Re system[3,42,43,44]. Their measured phase diagrams are quite different in terms of the number and homogeneity ranges of the ternary intermetallic compounds.
The experimental data mainly considered in the present work are the phase equilibria of the Ni-Mo-Re system at 1473 and 1873 K determined by Yaqoob and Joubert[3] utilizing EPMA and XRD. The equilibrium annealing treatments for the alloys were at 1873 K for 9 h and at 1473 K for 70 d. The crystal structure identification of the ternary intermetallic compounds was carried out and two unknown ternary compounds were observed. One phase has a body-centered tetragonal crystal structure with a structure prototype Mo
The phase equilibria at 1425 K were determined by Borisov et al. and Slyusarenko et al. using equilibrated alloys. The annealing time for the samples was 33.3 d[42,43]. The obtained isothermal section shows good compatibility with the work of Yaqoob and Joubert[3], except that only one ternary intermetallic compound was found. Borisov et al. and Slyusarenko et al. probably misinterpreted two phases as one single phase without performing phase identification[42,43]. Generally, these experimental data are considered reliable data.
The isothermal sections proposed by Kodentsov et al. and Feng et al. show poor agreement with that from Yaqoob and Joubert[3] and are therefore not utilized in the present assessment[41,44].
The site occupancies of the Ni-Mo-Re
Chekhovskoi et al. measured the CP of the NMR-75 alloy (75 wt.% Ni, 15 wt.% Mo and 10 wt.% Re) in a temperature range of 300-1300 K. However, the results were not used in the present work since it was difficult to reproduce if other data were to be considered simultaneously[45].
FIRST-PRINCIPLES CALCULATIONS
First-principles calculations were performed using the Vienna ab initio simulation package (VASP) with plane-wave basis sets[56] based on density functional theory (DFT)[57]. Projector augmented wave pseudopotentials[58] were adopted to represent the valence electrons. GGA-PW91[59] was adopted to describe the exchange and correlation effects. A large plane-wave cutoff energy of 400 eV was set for the plane-wave basis. The Monkhorst-Pack scheme[60] was used to construct the k-point meshes for Brillouin zone sampling. The spin-polarized calculations were performed with ferromagnetism set. The convergence criteria for electronic self-consistency and ionic minimization were 10
For the bcc, fcc and hcp solid solutions, the SQS method[62,63] was adopted to generate disordered structures for the VASP calculations. Supercells containing 16 atoms were constructed considering the configurations A12B4 and A15B1, where "A" denotes Ni for fcc, Mo for bcc and Re for hcp. Note that possible unstable structures, such as fcc Mo15Ni1, were not calculated since the full relaxation may not maintain the original structures. The total number of k-points multiplied by the total number of atoms per unit cell was at least 7200 for fcc, 6336 for bcc and 8000 for hcp. Using VASP, the SQS supercells were first relaxed with respect to cell volume only, then to volume and cell shape, and finally simultaneously to volume, cell shape and atomic position (i.e., full relaxation) in the present work. On this basis, a fast convergence speed can be achieved. To check the symmetry preservation, the radial distribution functions were analyzed[64].
In addition, VASP calculations were also performed to obtain the formation energies of all the end-members of the
THERMODYNAMIC MODELS
In the Ni-Mo-Re system, the stable phases included in this assessment are liquid, fcc, bcc, hcp,
Crystallographic and model information of stable phases in Ni-Mo-Re system
| Phase | Pearson symbol | Prototype | Model |
| Liquid | - | - | (Ni, Mo, Re) |
| fcc_A1 | cF4 | Cu | (Ni, Mo, Re) |
| bcc_A2 | cI2 | W | (Ni, Mo, Re) |
| hcp_A3 | hP2 | Mg | (Ni, Mo, Re) |
| oP56 | NiMo | (Ni) | |
| Ni | oP8 | Cu | (Ni, Mo) |
| Ni | tI10 | Ni | (Ni) |
| tP30 | CrFe | Enthalpy of formation for | |
| cI58 | 1473K and 1873K, enthalpy of formation | ||
| bct | tI56 | Mo | (Mo, Re) |
Solution phases
The solution phases (including liquid, fcc, bcc and hcp) were treated as substitutional solutions and described by a substitutional solution model with the Redlich-Kister polynomials[68].
Normally, for the interaction parameter, a linear temperature dependence is sufficient, i.e.,
Intermetallic phases
In the present work, three intermetallic phases, i.e.,
The molar Gibbs energy of each intermetallic phase
where
Although the Ni
For non-stoichiometric phase Ni
Following the previous assessment for the Ni-Mo binary, the
The end-members of the
Because of the limited solubility range reported by Heijwegen and Rieck[12], Kobayashi et al. and Zhu et al., the Ni
where the parameters c and d were obtained from the
There exist two intermetallic phases (i.e.,
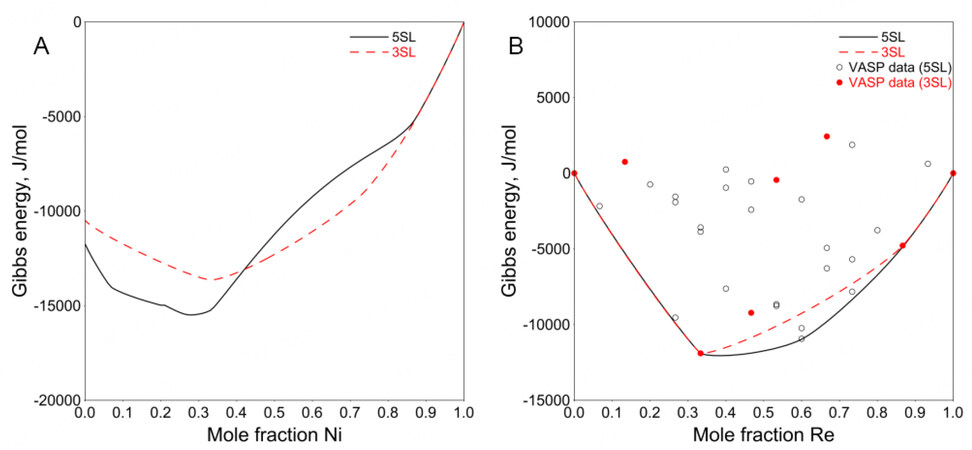
Figure 1. Calculated Gibbs energy of
The simplified 3SL fails to capture this structural relationship using the VASP data (mainly representing nearest-neighbor interactions) only. One can use positive interaction parameters within a sublattice to produce the composition sets. However, since there are only 23 binary end-members in the 3SL model, no suitable interaction parameters can be used to adjust the composition sets according to the experimentally determined composition range. For a detailed explanation, see Appendix I.
Therefore, the 5SL model combined with the VASP data was adopted in the present work to ensure reasonable modeling of the
The Gibbs energy of an end-member of
where
This simplification reduces the number of model parameters remarkably. It is necessary because it is difficult to determine the entropy of ABCDE in the
For
The
The unit cell of the bct phase contains 56 atoms distributed over six sites with CNs of 10, 12, 14 and 15. The sites with low CNs of 10 and 12 are shared by small and intermediate size atoms (Si and Co, respectively), the site with a CN of 14 is occupied by intermediate and large atoms (Co and Mo, respectively) and the site with a CN of 15 contains large atoms (Mo). Based on the observed XRD pattern and EPMA-determined composition of the phase, Yaqoob[2] removed the intermediate size Re from the site with a CN of 10 and placed it on the site with a CN of 15 along with Mo. Therefore, the bct phase was described using a 3SL model of (Mo, Re)
The Gibbs free energy of bct is expressed by Eq. (1) and one of its end-members I is described by:
where the parameter a was fixed to the DFT data calculated by Yaqoob[2]. The parameter b, corresponding to the entropy of formation of the end-members, was assessed together with the excess Gibbs energy based on phase equilibrium data.
RESULTS AND DISCUSSION
For solution phases, in the first step, the a terms for the interaction parameters were assessed using the SQS and measured enthalpy. In the second step, the b terms representing the influence of temperature on the interaction parameters were assessed based on the phase diagram and activity data.
For intermetallics, the enthalpy terms for the end-members were fixed to the VASP calculated data, while the entropy terms of the end-members were assessed based on the phase diagram data. As a final step, all parameters may be adjusted slightly to fit the experimental data better.
The thermodynamic parameters for phases in the present work are listed in Appendix II. A full database for the Ni-Mo-Re ternary system is provided in the supplementary material.
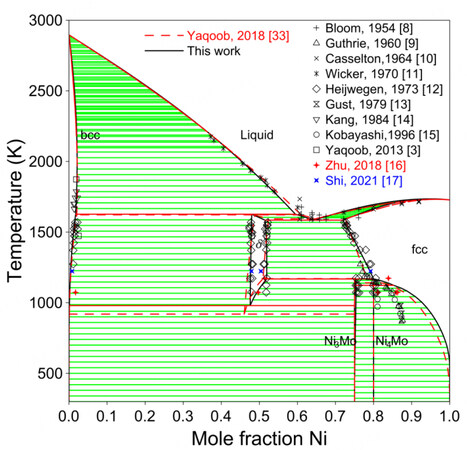
Ni-Mo system
In general, the assessment of Zhou et al. is not as satisfactory as that of Yaqoob et al.[32,33]. Therefore, only the results of Yaqoob et al. are compared with the present work in the following discussion. Figure 2 shows the calculated phase diagram compared with experimental data[8-17], as well as the previous assessment[33]. The experimental data that were not mentioned by Yaqoob et al. are colored. It is difficult to fit the homogeneity domain of the
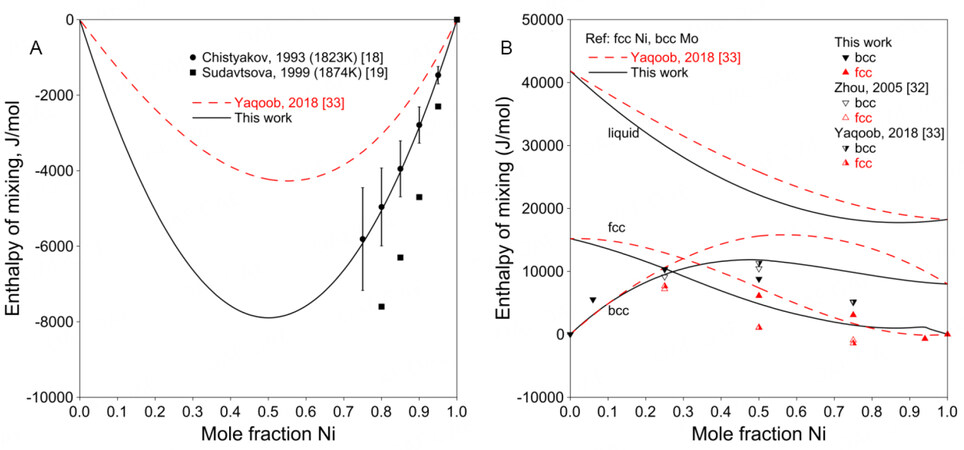
Figure 3A shows the enthalpy of mixing for the liquid phase. Chistyakov et al. and Sudavtsova measured the enthalpy of mixing of liquid using calorimetry at 1823 and 1874 K, respectively[18,19]. The experimental results from Sudavtsova are lower than those from Chistyakov et al.[18,19]. It is difficult to estimate which one is better. In the present assessment, Sudavtsova's results were found to be too negative that the bcc liquidus would be higher than the experimental data when the temperatures for invariant reactions were fixed. Moreover, considering that the experimental procedure of Chistyakov et al. was more detailedly described than that by Sudavtsova, the results from Chistyakov et al. were adopted in the present work[18].
Figure 3. (A) Assessed enthalpy of mixing for liquid at 1873 K compared with experimental data. (B) Assessed enthalpy of mixing for solution phases at 298 K compared with SQS results for Ni-Mo system.
Figure 3B shows the assessed enthalpies of mixing for solution phases at 298 K compared with the SQS data[32,33]. As noted above, the SQS calculations were performed only for stable structures in the present work, since possible unstable structures, such as fcc Mo or bcc Ni, may not be maintained during the full relaxation. Therefore, the SQS enthalpies of mixing from Zhou et al. and Yaqoob et al. were not used in the assessment[32,33]. Figure 3B shows a positive enthalpy for the bcc phase, indicating instability at low temperatures, which is in accordance with the phase diagram shown in Figure 2, where there is less than 3.0 at.% Ni soluble in bcc Mo at low temperatures.
Figure 4A shows the assessed formation enthalpies of Ni
Mo-Re system
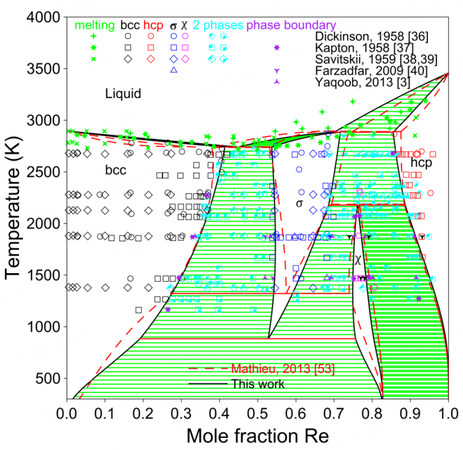
Knapton[37] conducted a careful study of this system by means of melting-point measurements, XRD and metallographic methods, using both powder-metallurgical and arc-melting samples. Knapton did not clarify which preparation method was used for each piece of data clearly. However, he showed that between 1673 and 1873 K, only the
As mentioned in the literature review, when extrapolating the Mo-Re system with the parameters of Mathieu et al. to the ternary system, the bcc phase of the three-phase equilibria (i.e., bcc +
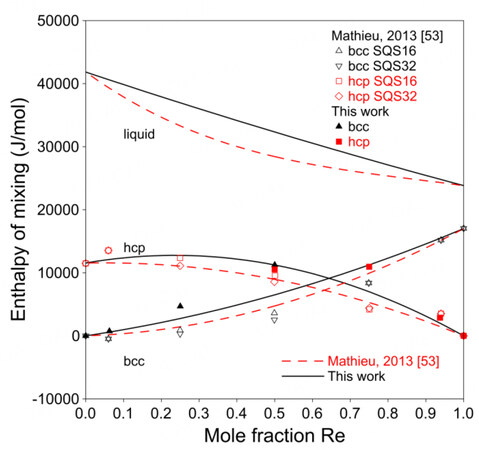
Figure 5 shows the present calculated phase diagram of the Mo-Re system and the assessment by Mathieu et al. together with the experimental data[3,36-40,53]. A larger
Figure 5. Assessed Mo-Re phase diagram compared with experimental data and assessment by Mathieu et al.[53].
Figure 6 shows the calculated enthalpies of mixing at 298 K together with the SQS data from Mathieu et al.[53].
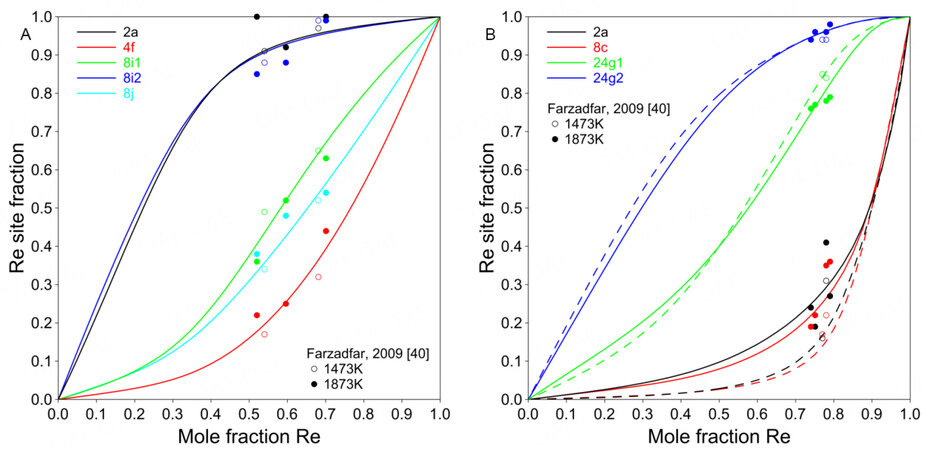
The present model can well predict the site fractions, as shown in Figure 7. Mathieu et al. did not use excess energy terms for the
Ni-Mo-Re system
Isothermal sections
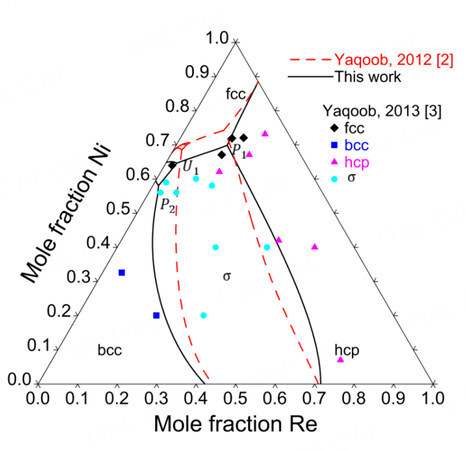
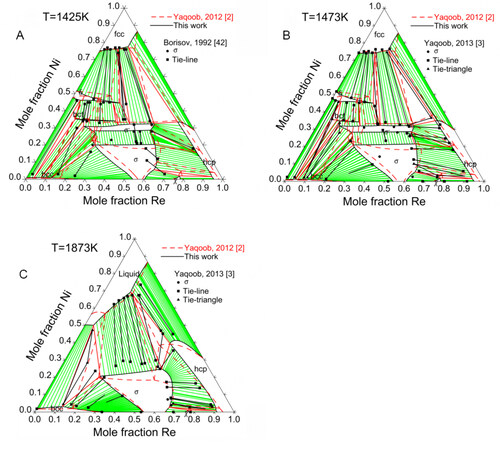
Figure 8 compares the assessed isothermal sections at 1425, 1473 and 1873 K with the experimental data. Since the Ni-Mo-Re system was assessed mainly based on the experimental data by Yaqoob et al., it is impossible to reproduce the phase equilibria concerning the
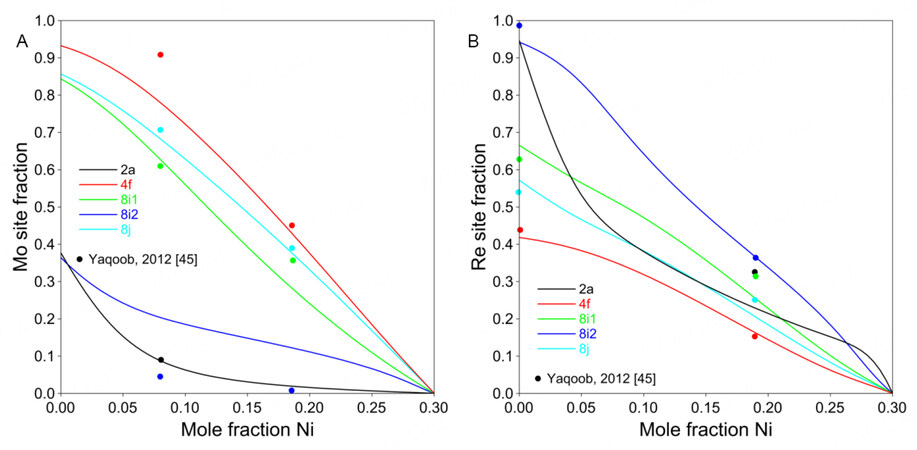
Figure 8. Calculated site fractions for Ni-Mo-Re
By applying the 5SL model, the site fractions and the ordering behavior of the ternary
Primary crystallization surface
The primary crystallization surface was assessed using the experimental data from Yaqoob et al. and presented in Figure 10, where there are five primary crystallization surfaces, namely, fcc, bcc, hcp,
CONCLUSIONS
The present work adopts the CALPHAD method to analyze a large amount of experimental and DFT data concerning the thermodynamics and phase diagrams of the Ni-Mo-Re alloy system. It demonstrates that the CALPHAD method can act as a practical appliance in the toolbox of materials informatics to assess various data by consistent modeling and then produce more useful data by computational predictions.
The Ni-Mo and Mo-Re binary systems were reassessed to obtain a better agreement with the experimental data. The large homogeneity range of the
Appendix I
By using the 5SL model for the sigma phase, positive values of the binary parameters
However, these end-members in the binary systems (such as NiMoMoMoMo and MoMoMoNiMo, see figures below) do not exist when using 3SL, so no interaction parameters can be used to adjust the MG. In conclusion, 3SL cannot reproduce the experimentally determined MG.
Appendix II
Thermodynamic parameters of the Ni-Mo-Re system assessed in the present work
Liquid
fcc
bcc
hcp
bct
DECLARATIONS
Authors' contributions
Writing and editing: Lei XH, Lu XG
First-principles calculations: Liu W
Data analysis and discussion: Lei XH, Liu W, Luo F, Lu XG
Availability of data and materials
Supplementary materials are available from the Journal of Materials Informatics or from the authors.
Financial support and sponsorship
The present work is supported by the National Key R & D Program of China (Grant No. 2017YFB0701502).
Conflicts of interest
The authors declared that there are no conflicts of interest.
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2022.
Supplementary Materials
REFERENCES
1. Reed RC. The superalloys fundamental and applications New York: Cambridge University Press; 2008.
2. Yaqoob K. Thesis. Paris-Est Créteil University, 2012. Available from: https://www.theses.fr/2012PEST1172.pdf[Last accessed on 29 Jul 2022].
3. Yaqoob K, Joubert J. Experimental investigation of the Mo-Ni-Re system. J Alloys Compd 2013;559:101-11.
4. J. -C. Crivello. Unpublished work.
5. Yaqoob K, Guénée L, Černý R, Joubert J. A modulated structure derived from the
6. Yaqoob K, Joubert J. Experimental determination and thermodynamic modeling of the Ni-Re binary system. J Solid State Chem 2012;196:320-5.
7. Grube G, Vosskühler H. Elektrische Leitfähigkeit und Zustandsdiagramm bei binären Legierungen. 8. Mitteilung. Das System Lithium-Zink. Z Anorg Allg Chem 1933;215:211-24.
8. Bloom DS, Grant NJ. An investigation of the systems formed by chromium, molybdenum, and nickel. JOM 1954;6:261-8.
9. P.V. Guthrie, E.E. Stansbury, X-ray and metallographic study of the nickel-rich alloys of the nickel-molybdenum system. Ⅱ, Oak Ridge National Laboratory, Oak Ridge, Tennessee, 1961, p. 57.
10. Casselton R, Hume-rothery W. The equilibrium diagram of the system molybdenum-nickel. J Less Comm Metals 1964;7:212-21.
11. A. Wicker, C. Allibert, J. Driole, E. Bonnier, Etude d' équilibres de phases dans les systèmes Ni-Nb-Mo, Ni-Nb et Ni-Mo, Comptes Rendus l'Acad. Sci. Sér. C 271 (1970) 273-275.
12. Heijwegen CP, Rieck GD. Determination of the phase diagram of the molybdenum-nickel system using diffusion couples and equilibrated alloys. Inter J Mater Res 1973;64:450-3.
13. W. Gust, T. Nguyen-Tat, B. Predel, untersuchungen zur dikontinuierlichen ausscheidung in einer Ni-Mo-Legierung mit 17.5 at. % Mo, Z. Metallkd. 70 (1979) 241-246.
14. Kang SL, Song Y, Kaysser WA, Hofmann H. Determination of Mo solidus in the Mo-Ni system by electrolytic phase separation method. Inter J Mater Res 1984;75:86-91.
15. Kobayashi S, Sumi T, Koyama T, Miyazaki T. Determination of coherent phase boundaries in Ni-V and Ni-Mo alloys by utilizing macroscopic composition gradient. J Japan Inst Metals 1996;60:22-8.
16. Zhu L, Wei C, Jiang L, Jin Z, Zhao J. Experimental determination of the phase diagrams of the Co-Ni-X (X = W, Mo, Nb, Ta) ternary systems using diffusion multiples. Intermetallics 2018;93:20-9.
17. Shi J, Guo C, Li C, Du Z. Experimental investigation of intermetallics and phase equilibria in the Hf-Mo-Ni system at 1100 ℃ and 950 ℃. Metall Mater Trans A 2021;52:1059-76.
18. ChistyakovLS, Grigorovich KV, Stomakhin AY. Enthalpy of formation of liquid Ni-Mo alloys, Izv. Vyss. Uchebn. Zaved. Chern. Metall 1993:82-83.
19. Sudavtsova VS. Thermodynamic properties of melts of Ni-Cr(Mo, W) binary systems, Russ. Metall 1999:118-120.
20. Spencer P, Putland F. A calorimetric study of intermediate phases in iron +, cobalt +, and nickel + molybdenum. J Chem Thermodyn 1975;7:531-6.
21. Kubaschewski O, Hoster T. Bildungs- und Umwandlungs-Enthalpien in binären und ternären Systemen der Metalle Eisen, Kobalt, Nickel und Molybdän. International J Mater Res 1983;74:607-9.
22. Norem, WE, Ph. D. Thesis. University of Tennessee, Knoxville, 1965.
23. Brooks CR, Meschter PJ. A Combined Thermodynamic Study of Nickel-Base Alloys, Department of Energy, Knoxville, Tennessee, 1981, p. 42.
25. Katayama I, Shimatani H, Kozuka Z. Thermodynamic study of solid Cu-Ni and Ni-Mo alloys by E.M.F. Measurements using the solid electrolyte. J Japan Inst Metals 1973;37:509-15.
26. Meshkov LL, Guzei LS, Sokolovskaya EM. Sokolovskaia, thermodynamics of nickel-molybdenum alloys. Russ J Phys Chem 1975;49: 1128-9. Available from: https://www.osti.gov/biblio/4035422[Last accessed on 29 Jul 2022].
27. Tsai HL. Thesis, University of Tennessee, 1983.
28. Pejryd L. Experimental study of phase equilibria and thermodynamic stabilitie in the system Ni-Mo-TiO2-O, Department of Inorganic Chemistry, University of Umeå, Umeå, Sweden, 1985.
29. Pejryd L. Phase relations and stabilities in the metal-rich part of the Ni-Mo-O system in the temperature range 1200-1400 K. Scand J Metall 1985;14:268-272.
30. Koyama K, Hashimoto Y, Suzuki K, Kameyama S. Determination of the standard gibbs free energy of formation of NiMo
31. Wang Y, Woodward C, Zhou S, Liu Z, Chen L. Structural stability of Ni-Mo compounds from first-principles calculations. Scripta Materialia 2005;52:17-20.
32. Zhou S, Wang Y, Jiang C, Zhu J, Chen L, Liu Z. First-principles calculations and thermodynamic modeling of the Ni-Mo system. Mater Sci Eng 2005;397:288-96.
33. Yaqoob K, Crivello J, Joubert J. Thermodynamic modeling of the Mo-Ni system. Calphad 2018;62:215-22.
34. Khan F, Asgar M, Nordblad P. Magnetization and magnetocrystalline anisotropy of Ni-Mo single crystal alloys. J Magn Magn Mater 1997;174:121-6.
35. Ghosh S, Das N, Mookerjee A. Magnetic properties of Ni-Mo single-crystal alloys; theory and experiment. J Phys : Condens Matter 1998;10:11773-80.
37. A.G. Knapton, J. Inst. Met. 87 (1958-1959) 62-64.
38. E.M. Savitskii, M.A. Tylkina, K.B. Povarova, Zh. Neorg. Khim. 1959;4: 424-34.
39. E.M. Savitskii, M.A. Tylkina, K.B. Povarova, Russ. J. Inorg. Chem. 4 (1959) 190-195.
40. Farzadfar S, Levesque M, Phejar M, Joubert J. Thermodynamic assessment of the molybdenum - rhenium system. Calphad 2009;33:502-10.
41. Kodentsov AA, Dunae SF, Slyusarenko EM, Sokolovskaya EM, Priimak AN. Phase equilibria in the rhenium-molybdenum-nickel system. Vestnik Moskovskogo Universiteta Ser. 2 Khimiya, 1987;28: 153-8.
42. Borisov VA, Yaschenko AI, Slyusarenko EM, Dunaev SF. Moscow Univ. Chem. Bull. 1992;47: 76-9.
43. Slyusarenko E, Borisov V, Sofin M, Kerimov E, Chastukhin A. Determination of phase equilibria in the system Ni-V-Cr-Mo-Re at 1425 K using the graph method. J Alloys Compd 1999;284:171-89.
44. Feng Y. Determination of isothermal sections of the Co-Nb-Ni and Ni-Mo-Re ternary systems. Rare Metals 2008;27:83-8.
45. Yaqoob K, Crivello JC, Joubert JM. Comparison of the site occupancies determined by combined Rietveld refinement and density functional theory calculations: example of the ternary Mo-Ni-Re
46. Chekhovskoi VY, Peletskii VE. Thermophysical properties of 75Ni-15Mo-10Re alloy. High Temperature 2003;41:221-8.
48. Cui Y, Jin Z, Lu X. Experimental study and thermodynamic assessment of the Ni-Mo-Ta ternary system. Metall Mater Trans A 1999;30:2735-44.
49. Morishita M, Koyama K, Yagi S, Zhang G. Calculated phase diagram of the Ni-Mo-B ternary system. J Alloys Compd 2001;314:212-8.
50. Mao P, Han K, Xin Y. Thermodynamic assessment of the Mo-Re binary system. J Alloys Compd 2008;464:190-6.
51. Mao P, Han K, Xin Y. Corrigendum to "thermodynamic assessment of the Mo-Re binary system". J Alloys Compd 2009;482:557-8.
52. Yang Y, Zhang C, Chen S, Morgan D, Chang YA. First-principles calculation aided thermodynamic modeling of the Mo-Re system. Intermetallics 2010;18:574-81.
53. Mathieu R, Dupin N, Crivello J, et al. CALPHAD description of the Mo-Re system focused on the sigma phase modeling. Calphad 2013;43:18-31.
55. Boettinger WJ, Newbury DE, Ritchie NWM, et al. Solidification of Ni-Re peritectic alloys. Metall Mat Trans A 2019;50:772-88.
56. Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B Condens Matter 1996;54:11169-86.
57. Dreizler RM, Gross EKU. Density functional theory. Springer Berlin Heidelberg: Berlin, Heidelberg, 1990; Chapter 4, pp 43-74.
58. Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B 1999;59:1758-75.
59. Perdew JP, Wang Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys Rev B Condens Matter 1992;45:13244-9.
60. Monkhorst HJ, Pack JD. Special points for Brillouin-zone integrations. Phys Rev B 1976;13:5188-92.
62. Zunger A, Wei S, Ferreira LG, Bernard JE. Special quasirandom structures. Phys Rev Lett 1990;65:353-6.
63. van de Walle A, Tiwary P, de Jong M, et al. Efficient stochastic generation of special quasirandom structures. Calphad 2013;42:13-8.
64. Shin D, Arróyave R, Liu Z, Van de Walle A. Thermodynamic properties of binary hcp solution phases from special quasirandom structures. Phys Rev B 2006;74:024204.
65. Crivello J, Souques R, Breidi A, Bourgeois N, Joubert J. ZenGen, a tool to generate ordered configurations for systematic first-principles calculations: the Cr-Mo-Ni-Re system as a case study. Calphad 2015;51:233-40.
66. Sundman B, Shi P. SGTE pure element database, version 5.0, Thermo-Calc Software, Stockholm.
67. Zheng W, Lu X, He Y, Cui Y, Li L. Thermodynamic assessment of the Fe-Mn-Si system and atomic mobility of its fcc phase. J Alloys Compd 2015;632:661-75.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Lei XH, Liu W, Luo F, Lu XG. A thermodynamic database of the Ni-Mo-Re system. J Mater Inf 2022;2:11. http://dx.doi.org/10.20517/jmi.2022.15
AMA Style
Lei XH, Liu W, Luo F, Lu XG. A thermodynamic database of the Ni-Mo-Re system. Journal of Materials Informatics. 2022; 2(3): 11. http://dx.doi.org/10.20517/jmi.2022.15
Chicago/Turabian Style
Lei, Xiong-Hui, Wei Liu, Fenghua Luo, Xiao-Gang Lu. 2022. "A thermodynamic database of the Ni-Mo-Re system" Journal of Materials Informatics. 2, no.3: 11. http://dx.doi.org/10.20517/jmi.2022.15
ACS Style
Lei, X.H.; Liu W.; Luo F.; Lu X.G. A thermodynamic database of the Ni-Mo-Re system. J. Mater. Inf. 2022, 2, 11. http://dx.doi.org/10.20517/jmi.2022.15
About This Article
Copyright
Data & Comments
Data

 Cite This Article 10 clicks
Cite This Article 10 clicks













Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.