Research Article | Open Access | 22 Jun 2022

Estimating the performance of a material in its service space via Bayesian active learning: a case study of the damping capacity of Mg alloys

Views: 776 | Downloads: 671 | Cited:

Bofeng Shi¹

, ...

Dezhen Xue^*,1

J Mater Inf 2022;2:8.

10.20517/jmi.2022.06 | © The Author(s) 2022.

Author Information

Article Notes

Cite This Article

Abstract

In addition to being determined by its chemical composition and processing conditions, the performance of a material is also affected by the variables of its service space, including temperature, pressure, and frequency. A rapid means to estimate the performance of a material in its service space is urgently required to accelerate the screening of materials with targeted performance. In the present study, a materials informatics approach is proposed to rapidly predict performance within a service space based on existing data. We utilize an active learning loop, which employs an ensemble machine learning method to predict the performance, followed by a Bayesian experimental design to minimize the number of experiments for refinement and validation. This approach is demonstrated by predicting the damping properties of a ZE62 magnesium alloy in a service space defined by frequency, strain amplitude, and temperature based on the available data for other magnesium alloys. Several utility functions that recommend a particular experiment to refine the estimates of the service space are used and compared. In particular, the standard deviation is found to reduce the prediction error most efficiently. After augmenting the database with nine new experimental measurements, the uncertainties associated with the predicted damping capacities are largely reduced. Our method allows us to forecast the properties in the service space of a given material by rapid refinement of the predictions via experiment measurements.

Keywords

Ensemble learning, active learning, Mg alloys, damping, service space, Bayesian optimization

Download PDF 0 25

INTRODUCTION

High-throughput calculations and combinatorial experiments, together with data-driven approaches, are now widely employed to search for new materials with targeted properties in an accelerated manner^[1-5]. Such data-driven methodologies, including statistical inference, machine learning, and deep learning, usually serve as means to explore the vast, high-dimensional "material space" with unknown properties^[6-9]. These algorithms infer material properties from material descriptors or features, which essentially are functions of chemical compositions and processing conditions^[10-13].

In addition to the intrinsic properties of materials, a variety of environmental factors during the service process affect the performance of a material^[14]. The variables within the working environment form the so-called "service space". For example, the service space for ship steel may include temperature and flow velocity, which in turn influence the corrosion rate, whereas, for a superalloy, the variables can include temperature, engine speed, and pressure^[15,16]. Only after acquiring the performance in the whole service space can a rational selection of the material be made as the material space is too vast to explore exhaustively and the service space can be complex. The emphasis of current materials informatics approaches has largely been on down selecting or exploring the material space, with few studies having explored the service space systematically and efficiently.

Machine learning offers an approach to address the complexity of both the materials and service spaces^[17-19]. Predictive machine learning models map the materials descriptors to performance, and the experimental design selects optimal candidates for experiments to minimize the overall effort^[20]. In experimental studies in materials science, the size of the available data is typically small, which often degrades the prediction as the uncertainties are then large^[21]. Adaptive sampling provides an efficient means to explore the vast search space and has been utilized to overcome the limitations of small training data sets and large model uncertainties^[20,22-25]. Incorporating efficient sampling methods to guide new measurements iteratively refines the service space in the fewest number of measurements.

Here, we propose an active learning approach that employs an ensemble machine learning method to predict the performance in the whole service space and then use Bayesian experimental design to recommend candidates for experiments. Our experimental design suggests an experiment as a function of one variable in the service space. This is in contrast to fixing all the variables to given values, which is the usual approach employed with functions such as Efficient Global Optimization^[26,27].

We demonstrate our approach by predicting the damping capacity of magnesium alloys in their service space. It is known that magnesium alloys exhibit good damping properties due to the easy motion of dislocations and weak pinning effects on dislocations^[28]. They have wide applications in structures ranging from aircraft to electrical devices, which usually require noise/vibration reduction and shock absorption^[29]. The alloying elements, including Zr, Zn, Cu, Ca, and rare earth elements, form secondary phases, introduce point defects and modify the grain size, which affect the damping properties of the alloy^[30-32]. These possible variations in chemistry lead to a vast material space for magnesium alloys. More importantly, the mobility of crystalline defects, such as dislocations and twin boundaries, depends on environmental variables, such as frequency ($$ f $$), strain amplitude ($$ \varepsilon $$), and temperature ($$ T $$), resulting in different damping capacities^[33-37]. These variables form the service space for the damping capacity.

We use an ensemble learning model to estimate the damping capacity in the three-dimensional space of $$ f $$, $$ \varepsilon $$, and $$ T $$ with different compositions. The model is then applied to the recently developed magnesium alloy ZE62, which shows promise with good mechanical and functional properties^[38]. Six different utility functions are used to recommend experiments to reduce the uncertainties of the predictions. It is found that maximizing the standard deviation of the experiment is the most efficient method. Guided by the utility functions, we iteratively augment the data from nine new experimental measurements and find that the uncertainties associated with the predicted damping capacities are largely reduced. Our approach provides a framework to predict the service space of materials in the search space and allows the predictive algorithm to choose the experiment from which it learns more efficiently with less training data.

MATERIALS AND METHODS

Experimental methods

Our ensemble learning model is applied to the recently developed as-cast Mg-6Zn-2RE (wt.%) alloy (ZE62). Specifically, ZE62 was prepared from pure Mg (99.99%), pure Zn (99.99%), and rare earth elements (Gd, Nd, Ce, and Y) in a resistance furnace. The 20.00 $$ \times $$ 3.50 $$ \times $$ 1.00 mm$$ ^3 $$ samples for damping measurements were obtained by spark-cutting. The damping capacity as a function of frequency, strain amplitude, and temperature was measured in a single cantilever model by a TA DMA 850 device.

Machine learning methods

We trained five supervised machine learning models on samples in the training set to map the material features and variables in the service space to the property. The models included a support vector machine with a radial-based kernel function, random forest, polynomial regression, neural network, gradient boosting decision tree, and extreme gradient boosting. The latter two are tree-based ensemble models, whereas the others are standard supervised models. These models were implemented in the e1071, stats, randomForest, nnet, gbm and xgboost packages within the RSTUDIO environment based on R-4.0.4. The details of the machine learning methods are listed in Table 1.

Table 1

Details of machine learning methods used in the present study

Model	Packages	Parameters
svr.rbf	e1071	The kernel function is a radial-based kernel function. The parameter gamma is equal to 1 and the cost is equal to 30
rf	randomForest	The number of trees is 500
poly	stats	The powers for dif.Esurf, dif.Emelt, and dif.Ymod are 2, 3, and 3, respectively. The powers for strain, temperature, and frequency are 2, 3, and 1, respectively
nnet	nnet	The size of the neural network is 50
gbm	gbm	The number of trees is 300 and the interaction depth is set as 5
mxgb	xgboost	The maximum depth of trees is 6 and the evaluation metric is the rooted mean squared error

RESULTS AND DISCUSSION

Design strategy

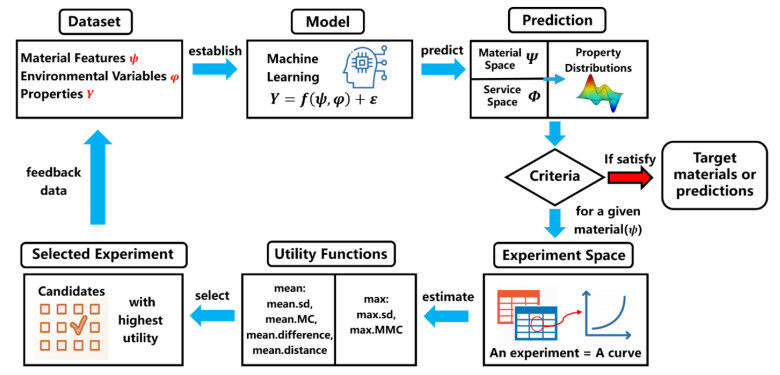
Figure 1 shows our design strategy, including prediction and optimization. It employs machine learning algorithms to build surrogate models from existing data to predict outcomes within the service space of all unexplored materials in the material space. The optimization part recommends a candidate experiment by Bayesian optimization. The candidate experiment consists of several measurement values with only one variable changing in the service space. The new data augment the training data.

Estimating the performance of a material in its service space via Bayesian active learning: a case study of the damping capacity of Mg alloys

Figure 1. Flowchart of our design strategy including prediction and optimization.

A database with known material features ($$ \psi $$), environmental variables belonging to the service space ($$ \varphi $$), and damping capacity as the target property ($$ Y $$), serves to build the machine learning model, $$ Y=f(\psi , \varphi )+\varepsilon $$. All the unexplored materials with material features ($$ \psi $$) known form the material space and each material in the space possesses a service space with known variables $$ \varphi $$, such as temperature, frequency, and so on. The machine learning model $$ Y=f(\psi , \varphi )+\varepsilon $$ is directly applied to an unexplored new material ($$ \psi $$ is known) to obtain its service space, as the variables $$ \varphi $$ are discretized within an allowed range. The output of the prediction can be the service space of all possible materials. Since the prediction inevitably contains uncertainties, for a material of interest, utility functions (or selectors) can be employed to select an experiment and then augment the database with more accurate data to efficiently reduce the model uncertainties. An experiment here is a measure of damping capacity as a function of one of the variables (frequency, strain amplitude, or temperature), i.e., the damping curve. There are thousands of experiments that could be completed in the three-dimensional service space, which we refer to as the "experimental space". The focus here is to select the meaningful experiment that can significantly reduce the uncertainties. Once the selected experiment is performed, the results are added to the initial training data and the loop repeats.

Data and feature selection

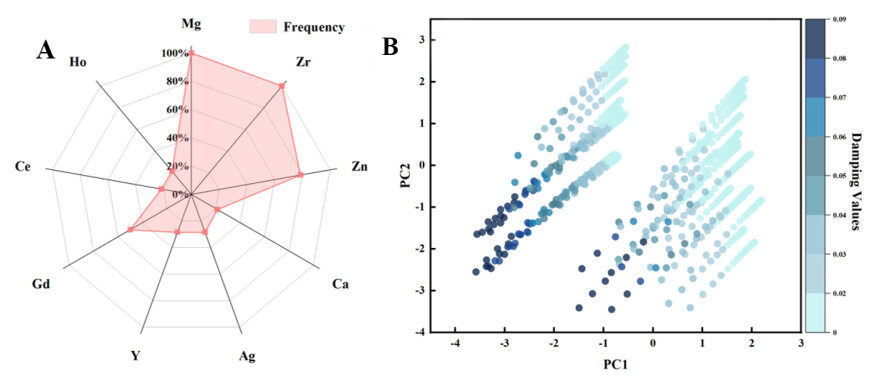
We built a training dataset containing 769 data points with known damping capacity. The data are from 14 as-cast magnesium alloys. The distribution of different alloying elements in the training data is shown in the radar chart in Figure 2A. The principal elements, Mg, Zr, and Zn, are the most common. It is noteworthy that although our test alloy, ZE62, contains Nd, which is absent from the training data, our model can make predictions of alloys containing Nd. The damping capacity was obtained for 40 experiments, in which it varies with one of the variables, namely, frequency ($$ f $$), strain amplitude ($$ \varepsilon $$), or temperature ($$ T $$). As shown in Figure 2B, all the samples in the training data were visualized in the plane of two principal components, which were obtained by principal component analysis. The trend in the damping property of the 40 experiments can be clearly identified in the plane. The damping values of the Mg alloys range from 0 to 0.1 in the training dataset, as indicated by the color bar in Figure 2B.

Figure 2. Visualization of training dataset for damping capacity of magnesium alloys used. (A). Distribution of different elements in training data. (B). Distribution of samples in training data in the plane of two principal components (PC1 and PC2). The color indicates the damping values.

Both the chemical compositions and environmental variables strongly affect the damping capacity of magnesium alloys. Two sets of independent variables are thus needed to serve as the inputs to the surrogate model, namely, the material features ($$ \psi $$) and the service space variables ($$ \varphi $$).

The compositions of different elements can potentially be used as material features, but this leads to a high-dimensional feature space, as well as poor interpretation of the surrogate model. More importantly, the model based on chemical composition usually has a poor capability to generalize, especially when there are new elements in the unexplored search space. We thus establish a material features pool based on 12 physical properties of elements, as listed in Table 2. The mole average of the physical properties is calculated via $$ \psi _{ave}=\sum_{i=1}^n w_i p_i $$, where $$ w_i $$ is the mole fraction of the $$ i^{th} $$ element and $$ p_i $$ is the physical property of the $$ i^{th} $$ element. The physical properties due to different elements in the alloy are calculated using $$ \psi _{diff}=\sqrt{\sum_{i=1}^n w_i (1-\frac{p_i}{\psi _{ave}} )^2 } $$. In total, there are 24 material features listed in Table 2.

Table 2

Physical properties of elements and material features $$ \psi $$

Properties of elements	Material features ($$ \boldsymbol{\psi} $$)
Melting point (K)	ave.Tm
Melting point (K)	dif.Tm
Electronegativity (Martynov and Batsanov)	ave.elgMB
Electronegativity (Martynov and Batsanov)	dif.elgMB
Cohesive energy (J/mol)	ave.Ecoh
Cohesive energy (J/mol)	dif.Ecoh
1st ionization energy (kJ/mol)	ave.1Eion
1st ionization energy (kJ/mol)	dif.1Eion
2nd ionization energy (kJ/mol)	ave.2Eion
2nd ionization energy (kJ/mol)	dif.2Eion
Enthalpy of melting (kJ/mol)	ave.Emelt
Enthalpy of melting (kJ/mol)	dif.Emelt
Enthalpy of surface (Miedema) (kJ/mol)	ave.Esurf
Enthalpy of surface (Miedema) (kJ/mol)	dif.Esurf
Metallic radii (Å)	ave.Rmet
Metallic radii (Å)	dif.Rmet
Valence electron number	ave.venum
Valence electron number	dif.venum
Work function (eV)	ave.wf
Work function (eV)	dif.wf
Young's modulus (GPa)	ave.Ymod
Young's modulus (GPa)	dif.Ymod
Atomic mass	ave.atmass
Atomic mass	dif.atmass

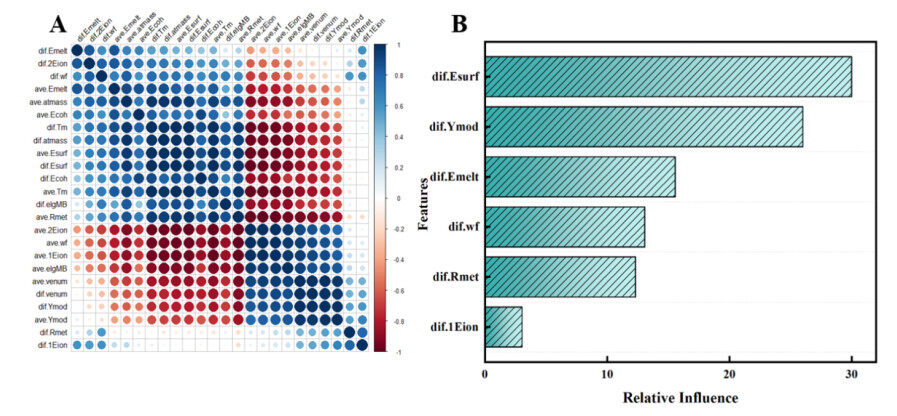
As shown in Figure 3A, certain features are highly correlated, and we filter out several using Pearson correlation analysis. The correlation coefficients between feature pairs are calculated and lie in the interval [0, 1]. We consider feature subsets with coefficients larger than 0.8 as highly correlated and remove others. We are left with six features if we consider that the difference between elements can potentially play an important role in modifying the properties of the principal elements. We use gradient tree boosting to calculate their influence on the property. The ranking of the 6 features is shown in Figure 3B, and we select the top three material features ($$ \psi $$), namely, dif.Esurf, dif.Ymod and dif.Emelt, as inputs to the surrogate model.

Figure 3. Pearson correlation and relative influence of features. (A). Graphical representation of Pearson correlation matrix for the 24 material features. Blue and red indicate positive and negative correlations, respectively. The darker the tone and the larger the circle, the more significant the corresponding correlation. (B). Relative influence of features according to gradient boosting, which indicates the impact of features on the property. These features are preselected by Pearson filtering.

The service space variables ($$ \varphi $$) include the frequency ($$ f $$), strain amplitude ($$ \varepsilon $$), and temperature ($$ T $$). Generally, damping values increase with increasing strain due to the larger driving force for defects to move^[28]. However, there is no general tendency for the damping capacity of magnesium alloys with temperature or frequency^[31,33]. Here, we discretize these factors and set up a three-dimensional service space with discretized variable values. The temperature ranges from 273.15 to 373.15 K in steps of 5 K. The frequency varies from 1 to 20 Hz in steps of 1 Hz. The strain amplitude changes from 10$$ ^{-5} $$ to 10$$ ^{-3} $$ logarithmically.

Machine learning models

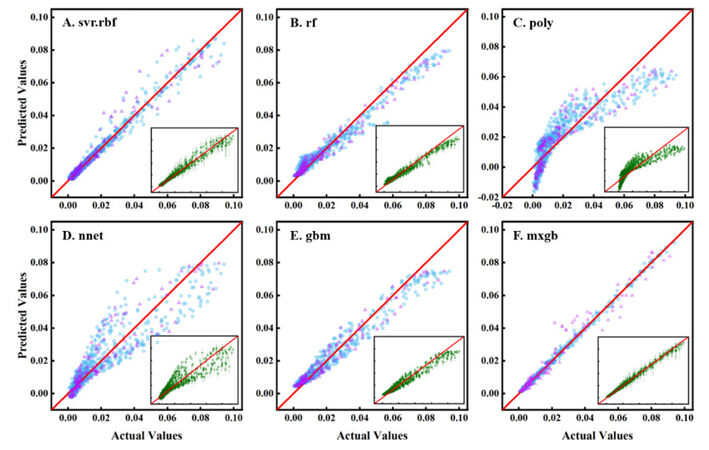
We employ five different machine learning models to estimate the damping capacity, including a support vector machine with a radial basis function kernel (svr.rbf), a random forest regression tree model (rf), a polynomial regression model (poly), a neural network (nnet) and a gradient boosting model (gbm). The original dataset is split into two parts, i.e., 80% for the training set and the remaining 20% for the testing set. The model performance can be visualized by plotting the predicted damping capacity as a function of the measured values. Figure 4A-E show the performance of the 5 models, where the blue points represent the training set and the purple points are the testing set. The testing data show varying degrees of deviation from the diagonal, especially for the single supervised regression models.

Figure 4. Performance of machine learning models. The predicted damping capacity is plotted as a function of the measured values. The blue dots represent the training set and the purple dots are for the testing set. (A). Support vector regression with radial basis function kernel (svr.rbf). (B). Random forest regression tree model (rf). (C). Polynomial regression model (poly). (D). Neural network (nnet). (E). Gradient boosting model (gbm). (F). Ensemble learning model of extreme gradient boosting (mxgb). The insets show the mean and standard deviation of the predicted value obtained by the bootstrap resampling method.

Here, we also use the boosting method of ensemble learning, which uses decision trees as base learners and then integrates the outcomes from these learners for a more accurate predictive model. The extreme gradient boosting algorithm (mxgb) is employed and its performance is shown in Figure 4F. The data points are distributed about the diagonal line, suggesting that the model is reasonably good.

We further evaluate the performance of the models by estimating the training and test errors. All data in the dataset are used to train the regression model and obtain the prediction for each sample. The training error is calculated by comparing the prediction ($$ \widehat{y}_{i}$$) and the measured values ($$ y_i $$) of all samples ($$ n $$) in the dataset, which is given by $$ RMSE.train= \sqrt{\frac{1}{n} \sum_{i=1}^n (y_i-\widehat{y}_{i})^2 } $$. As shown in Figure 5A, the ensemble learning model of the mxgb outperforms the other models in terms of training error.

Figure 5. Performance of different models in terms of training and test errors. (A). Training error of RMSE.train. (B). Test error of RMSE.boots. (C). Test error of RMSE.cv. The ensemble learning model of the extreme gradient boosting (mxgb) outperforms the other models.

The cross-validation and the bootstrap method with replacement are employed to estimate the test error for these models. Bootstrap resampling is commonly used to evaluate the robustness of models. It is implemented by sampling the data with replacement. In the present study, we sample $$ n = 769 $$ observations from the initial dataset containing 769 points of damping properties. We repeated the process 500 times and generated 500 resampled training sets to build 500 machine learning models. Each sample in the initial dataset thus gives 500 predicted values, which are used to determine the mean value ($$ \mu _i $$) and associated standard deviation ($$ \varepsilon _i $$). The insets in Figure 4 show the mean value ($$ \mu _i $$) as a function of measured value ($$ y_i $$) and the error bar gives the standard deviation ($$ \varepsilon _i $$). Again, the mxgb shows a tight distribution about the diagonal line. The mean squared error from $$ \mu _i $$ can be considered as an estimate of the training error and is given by $$ RMSE.boots=\sqrt{\frac{1}{n} \sum_{i=1}^n (y_i-\mu _i )^2 } $$. We utilized leave-one-out cross-validation (LOOCV) to estimate the test error, which is given by $$ RMSE.cv= \sqrt{\frac{1}{n} \sum_{m=1}^n-(y_m-\widehat{y}_{m})^2 } $$, where $$ \widehat{y}_{m} $$ is the prediction of the $$ m^{th} $$ leave out sample. When calculating the LOOCV error, we used all the training data. The $$ RMSE.cv $$ and $$ RMSE.boots $$ are shown in Figure 5B and C, respectively. The mxgb possesses the lowest test error and outperforms the other machine learning models.

We used the mxgb model to estimate the damping capacity of unexplored magnesium alloys in the service space of frequency ($$ f $$), strain amplitude ($$ \varepsilon $$), and temperature ($$ T $$). The recently developed ZE62 magnesium alloy, which is absent in our training dataset, is utilized as a test alloy. The material features ($$ \psi $$) including dif.Esurf, dif.Ymod, and dif.Emelt are calculated according to the chemical compositions of the ZE62 alloy and the service space variables ($$ \varphi $$)$$ f $$, $$ \varepsilon $$, and $$ T $$ are discretized within the preset range. The damping capacity of ZE62 in its service space is estimated and the results are shown in Figure 6. This can be used to decide whether the ZE62 alloy is suitable for particular applications or to determine the range of environment variables for a targeted damping value. However, as the data in the training set is insufficient, the estimates in Figure 6 are not necessarily accurate. Therefore, we augment the training set with several measured values of unexplored damping capacity in the service space to further reduce the uncertainties of the predictions.

Figure 6. Estimated damping capacity of ZE62 alloy in its service.

Efficient sampling in service space

The central question is which points in the service space in Figure 6 should be measured so that the uncertainties are reduced the most? In practice, during one experiment, we measure the damping capacity easily as a function of either frequency ($$ f $$), strain amplitude ($$ \varepsilon $$), or temperature ($$ T $$) rather than a single point in the service space. Therefore, the selection problem becomes one in which a particular experiment is recommended to measure a damping capacity curve in the service space. The continuous improvement of the estimate can be achieved via active learning, which recommends the most promising experiment with the largest utility function value in each iteration. The damping capacity curve then augments the data set for the next iteration. In the following, we compare the efficiency of six different utility functions in reducing the uncertainties associated with the estimates of damping capacity for ZE62. During each iteration, we measure the damping capacity values.

The first two utility functions consider the uncertainty associated with the damping capacity. We use the bootstrap resampling method to estimate the standard deviation ($$ sd $$) associated with the estimated damping capacity for each point ($$ x $$) in the service space. This is given by:

(1)

$$ \begin{equation} s d=\sqrt{\frac{1}{K} \sum\limits_{i=1}^{K}\left(y_{i}(x)-\bar{y}(x)\right)^{2}} \end{equation} $$

where $$ K $$ is the number of bootstraps, $$ y_i (x) $$ is the predicted value based on each resampled dataset and $$ \bar{y}(x) $$ is the mean value of the bootstrapped predictions. As each experiment contains several points in the service space, we either utilize the maximum of their $$ sd $$ values or the mean of their $$ sd $$ values as the utility function of the experiment. The former is abbreviated as max.sd, while the latter is abbreviated as mean.sd. The experiment with the highest sd values will be selected, measured, and then fed back to the dataset.

The next two utility functions consider the influence of how the points in the service space change the model, i.e., the change compared to the current model after augmenting the data of selected candidates. We would like to choose the experiment that can change the model most^[39]. The model change ($$ MC $$) for a point ($$ x $$) in the service space can be calculated through:

(2)

$$ \begin{equation} M C=\frac{1}{K} \sum\limits_{i=1}^{K}\left\|\left(f(x)-y_{i}(x)\right) \phi_{i}(x)\right\| \end{equation} $$

where $$ K $$ is the number of bootstraps, $$ f(x) $$ is the prediction of the ensemble model based on all the data, $$ y_i (x) $$ is the prediction from the model based on the $$ i^{th} $$ resampled subset and $$ \phi _i (x) $$ is a matrix containing the predicted results of each single model using the resampled subset. Similar to the case of $$ sd $$, we either utilize the maximum of the $$ MC $$ values of the points in an experiment or the mean of their $$ MC $$ values as the utility function of the experiment. They are abbreviated as max.MC and mean.MC, respectively.

Distance is another consideration for the utility function, which evaluates how "far" the new data point ($$ x $$) is from the known data ($$ \mathit{\boldsymbol{z}} $$). The farther the data points are, the greater the difference is from the known data. The distance is defined by the minimum Euclidean distance from point ($$ x $$) in the unexplored service space to the training data, given by:

(3)

$$ \begin{equation} {distance}=\underset{\forall x \in X} {min}\;{dist}(x, \mathit{\boldsymbol{z}}) \end{equation} $$

For an experiment with several points ($$ x $$), we calculate the mean value of distance for the points, which defines the utility function mean.distance. The concept here is to find the curve that is "farthest" from the known space.

Query by committee is a common approach in active learning and defines a promising candidate as one with the highest deviation amongst the predictions of different learners^[40]. The difference between different models is defined as the sum of deviation between the prediction and the mean value from the models:

(4)

$$ \begin{equation} { difference }=\sum\limits_{\alpha}\left(\hat{y}^{\alpha}(x)-\bar{y}(x)\right)^{2} \end{equation} $$

where $$ \alpha $$ represents the different learners, $$ \hat{y}^{\alpha}(x) $$ is the prediction of each single learner and $$ \bar{y}(x) $$ is the mean value of the predictions from different learners. We calculate the mean value of the difference for points from the experiment to define the utility function of mean.difference.

Therefore, in total, we propose six utility functions, namely, max.sd, mean.sd, max.MC, mean.MC, mean.distance and mean.difference. The next experiment ($$ e^* $$) is recommended by maximizing the value of the utility function ($$ \mathcal{U} $$), i.e.:

(5)

$$ \begin{equation} e^{*}=\underset{e \in {exper\; space }}{{argmax}} \mathcal{U}. \end{equation} $$

For comparison, a "random" selection that mimics the trial-and-error strategy is also considered. It selects an experiment randomly in the experiment space.

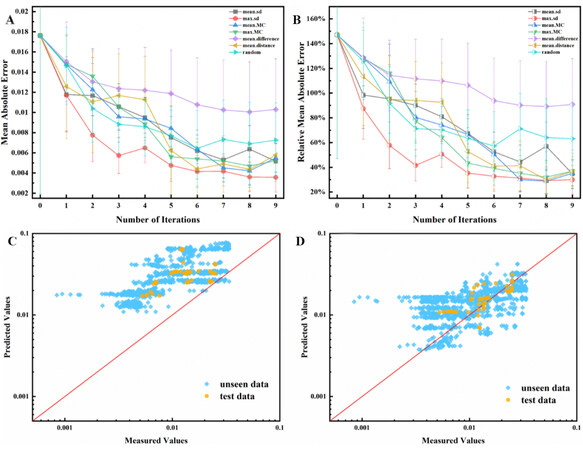
We perform seven experiments based on the seven selection criteria and augment the data, as shown in Figure 1. To evaluate the uncertainty reduction after each iteration, we select three experiments randomly to measure their damping capacities in advance. This is referred to as the "test data". The mean absolute error (MAE) and relative absolute error (RMAE) between the measured and predicted values of the points are utilized in evaluating the performance of the model in each iteration. Figure 7 shows the results after nine iterations. The MAE and RMAE are plotted in Figure 7A and B, respectively, as a function of iteration number. By augmenting more data, the errors in the utility functions decrease. However, the utility function max.sd has the best convergence rate and reduces the uncertainties in only a few iterations. Moreover, max.MC and mean.sd show a similar tendency to change the error. The mean.difference has the worst performance, which may be caused by the inaccurate estimates from the base learners leading to large differences.

Figure 7. Error changes for different selectors with increasing iterations. (A). Mean absolute error of selected untested experiments. (B). Relative mean absolute error of selected untested experiments. (C). Predicted value before refinement as a function of measured values. (D). Predicted values after refinement by the utility function of max.sd vs the measured values. The performance of the model is improved

Figure 7C and D show the model performance before and after refinement by Bayesian optimization, respectively. The refined model in Figure 7D is selected as the desired mxgb model after 9 iterations with sampling utility function max.sd. The data sampled from the other six sampling utility functions are "unseen" by the best performer and thus are also used to check the model performance. It can be seen that before the refinement, almost all the data points deviated from the diagonal line of the figure. This is reasonable, since the ZE62 alloy is fresh to the model and contains elements that are not present in the training data. After refinement, most data points distribute around the diagonal line showing an improvement in the model performance. Thus, estimates of the performance in the service space can be rapidly refined in a few iterations, even for those points where experimental data are lacking.

In summary, we propose a materials informatics approach to rapidly estimate the performance of an alloy within its service space. It employs an ensemble machine learning method to initially predict the performance in the service space and then, for refinement and validation, utilizes Bayesian experimental design to minimize the number of experiments, all within an active learning framework. We use the approach to predict the damping properties of a ZE62 magnesium alloy in the service space of frequency, strain amplitude, and temperature. Several utility functions are employed to recommend a particular experimental curve, and their efficiency in reducing the uncertainties in estimation is compared. The max.sd utility, which chooses an experiment with the highest standard deviation, is identified to reduce the prediction error of ZE62 the most. Although we only demonstrate here our approach for a single case study of damping capacity in a magnesium alloy, we expect the approach to be valid for other material systems.

Declarations

Authors' contributions

Methodology, software, investigation, writing - original draft: Shi B

Conceptualization, resources, writing - review & editing: Zhou Y

Resources, writing - review & editing: Fang D

Code checking, validation: Tian Y

Resources, supervision: Ding X

Resources, supervision: Sun J

Conceptualization, visualization, writing - review & editing: Lookman T

Conceptualization, visualization, writing - review & editing: Xue D

Availability of data and materials

The data used in the current study will be available from the corresponding author based on reasonable request.

Financial support and sponsorship

The authors gratefully acknowledge the support of National Key Research and Development Program of China (2021YFB3802102), National Natural Science Foundation of China (Grant Nos. 52173228 and 51931004) and the 111 project 2.0 (BP2018008).

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Ethical approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Copyright

REFERENCES

1. Zhang T. New tool in the box. J Mater Inf 2021;1:1.

2. Zhang T, Liu X. Informatics is fueling new materials discovery. J Mater Inf 2021;1:6.

3. Aggarwal R, Demkowicz MJ, Marzouk YM. Information-driven experimental design in materials science. In: Lookman T, Alexander FJ, Rajan K, editors. Information science for materials discovery and design. Cham: Springer International Publishing; 2016. pp. 13-44.

4. Himanen L, Geurts A, Foster AS, Rinke P. Data-driven materials science: status, challenges, and perspectives. Adv Sci 2019;6:1900808.

5. Ramakrishna S, Zhang T, Lu W, et al. Materials informatics. J Intell Manuf 2019;30:2307-26.

6. Schütt KT, Sauceda HE, Kindermans PJ, Tkatchenko A, Müller KR. SchNet - a deep learning architecture for molecules and materials. J Chem Phys 2018;148:241722.

7. Agrawal A, Choudhary A. Deep materials informatics: applications of deep learning in materials science. MRS Communications 2019;9:779-92.

8. Ramprasad R, Batra R, Pilania G, Mannodi-kanakkithodi A, Kim C. Machine learning in materials informatics: recent applications and prospects. npj Comput Mater 2017;3.

9. Nelson CT, Ghosh A, Oxley M, et al. Deep learning ferroelectric polarization distributions from STEM data via with and without atom finding. npj Comput Mater 2021;7.

10. Zhang Y, Wen C, Wang C, et al. Phase prediction in high entropy alloys with a rational selection of materials descriptors and machine learning models. Acta Mater 2020;185:528-39.

11. He J, Li J, Liu C, et al. Machine learning identified materials descriptors for ferroelectricity. Acta Mater 2021;209:116815.

12. Xue D, Balachandran PV, Wu H, et al. Material descriptors for morphotropic phase boundary curvature in lead-free piezoelectrics. Appl Phys Lett 2017;111:032907.

13. Weng B, Song Z, Zhu R, et al. Simple descriptor derived from symbolic regression accelerating the discovery of new perovskite catalysts. Nat Commun 2020;11:3513.

14. Callister, WD, Rethwisch DG. Materials science and engineering an introduction, 10th ed. John Wiley & Sons, Inc.; 2018.

15. Guedes Soares C, Garbatov Y, Zayed A. Effect of environmental factors on steel plate corrosion under marine immersion conditions. Corr Eng, Sci Technol 2013;46:524-41.

16. Stinville JC, Martin E, Karadge M, et al. Fatigue deformation in a polycrystalline nickel base superalloy at intermediate and high temperature: competing failure modes. Acta Mater 2018;152:16-33.

17. Iwasaki Y, Takeuchi I, Stanev V, et al. Machine-learning guided discovery of a new thermoelectric material. Sci Rep 2019;9:2751.

18. Kusne AG, Yu H, Wu C, et al. On-the-fly closed-loop materials discovery via Bayesian active learning. Nat Commun 2020;11:5966.

19. Yuan R, Tian Y, Xue D, et al. Accelerated search for BaTiO3-based ceramics with large energy storage at low fields using machine learning and experimental design. Adv Sci (Weinh) 2019;6:1901395.

20. Xue D, Balachandran PV, Hogden J, Theiler J, Xue D, Lookman T. Accelerated search for materials with targeted properties by adaptive design. Nat Commun 2016;7:11241.

21. Rickman J, Lookman T, Kalinin S. Materials informatics: from the atomic-level to the continuum. Acta Mater 2019;168:473-510.

22. Balachandran PV, Xue D, Theiler J, Hogden J, Lookman T. Adaptive strategies for materials design using uncertainties. Sci Rep 2016;6:19660.

23. Xue D, Xue D, Yuan R, et al. An informatics approach to transformation temperatures of NiTi-based shape memory alloys. Acta Mater 2017;125:532-41.

24. Gopakumar AM, Balachandran PV, Xue D, Gubernatis JE, Lookman T. Multi-objective optimization for materials discovery via adaptive design. Sci Rep 2018;8:3738.

25. Tian Y, Yuan R, Xue D, et al. Determining multi-component phase diagrams with desired characteristics using active learning. Adv Sci (Weinh) 2020;8:2003165.

26. Carpentier A, Lazaric A, Ghavamzadeh M, Munos R, Auer P. Upper-confidence-bound algorithms for active learning in multi-armed bandits. In: Kivinen J, Szepesvári C, Ukkonen E, Zeugmann T, editors. Algorithmic learning theory. Berlin: Springer Berlin Heidelberg; 2011. pp. 189-203.

27. Jones DR, Schonlau M, Welch WJ. Efficient global optimization of expensive black-box functions. J Glob Optim 1998;13:455-92.

28. Granato A, Lücke K. Theory of mechanical damping due to dislocations. J Appl Phys 1956;27:583-93.

29. Landkof B. Magnesium Applications in aerospace and electronic industries. In: Kainer KU, editor. Magnesium alloys and their applications. Weinheim: Wiley-VCH Verlag GmbH & Co. KGaA; 2000. pp. 168-72.

30. Yu L, Yan H, Chen J, Xia W, Su B, Song M. Effects of solid solution elements on damping capacities of binary magnesium alloys. Mater Sci Eng A 2020;772:138707.

31. Niu R, Yan F, Wang Y, Duan D, Yang X. Effect of Zr content on damping property of Mg-Zr binary alloys. Mater Sci Eng A 2018;718:418-26.

32. Tang Y, Zhang C, Ren L, et al. Effects of Y content and temperature on the damping capacity of extruded Mg-Y sheets. J Mag Alloys 2019;7:522-8.

33. Cui Y, Li J, Li Y, Koizumi Y, Chiba A. Damping capacity of pre-compressed magnesium alloys after annealing. Mater Sci Eng A 2017;708:104-9.

34. Wang J, Lu R, Qin D, Huang X, Pan F. A study of the ultrahigh damping capacities in Mg-Mn alloys. Mater Sci Eng A 2013;560:667-71.

35. Wang J, Li S, Wu Z, Wang H, Gao S, Pan F. Microstructure evolution, damping capacities and mechanical properties of novel Mg-xAl-0.5Ce (wt%) damping alloys. J Alloys Compd 2017;729:545-55.

36. Cui Y, Li Y, Sun S, et al. Enhanced damping capacity of magnesium alloys by tensile twin boundaries. Scr Mater 2015;101:8-11.

37. Somekawa H, Watanabe H, Basha DA, Singh A, Inoue T. Effect of twin boundary segregation on damping properties in magnesium alloy. Scr Mater 2017;129:35-8.

38. Chen Y, Tian Y, Zhou Y, et al. Machine learning assisted multi-objective optimization for materials processing parameters: a case study in Mg alloy. J Alloys Compd 2020;844:156159.

39. Cai WB, Zhang Y, Zhou J. Maximizing expected model change for active learning in regression : proceedings of IEEE 13th International Conference on Data Mining; 2013 Dec 7-10; Texas, USA. IEEE; 2013. p. 51-60.

40. Burbidge R, Rowland JJ, King RD. Active Learning for Regression Based on Query by Committee. In: Yin H, Tino P, Corchado E, Byrne W, Yao X, editors. Intelligent data engineering and automated learning - IDEAL 2007. Berlin: Springer Berlin Heidelberg; 2007. pp. 209-18.

Cite This Article

Export citation file: BibTeX | RIS

OAE Style

Shi B, Zhou Y, Fang D, Tian Y, Ding X, Sun J, Lookman T, Xue D. Estimating the performance of a material in its service space via Bayesian active learning: a case study of the damping capacity of Mg alloys. J Mater Inf 2022;2:8. http://dx.doi.org/10.20517/jmi.2022.06

AMA Style

Shi B, Zhou Y, Fang D, Tian Y, Ding X, Sun J, Lookman T, Xue D. Estimating the performance of a material in its service space via Bayesian active learning: a case study of the damping capacity of Mg alloys. Journal of Materials Informatics. 2022; 2(2): 8. http://dx.doi.org/10.20517/jmi.2022.06

Chicago/Turabian Style

Shi, Bofeng, Yumei Zhou, Daqing Fang, Yuan Tian, Xiangdong Ding, Jun Sun, Turab Lookman, Dezhen Xue. 2022. "Estimating the performance of a material in its service space via Bayesian active learning: a case study of the damping capacity of Mg alloys" Journal of Materials Informatics. 2, no.2: 8. http://dx.doi.org/10.20517/jmi.2022.06

ACS Style

Shi, B.; Zhou Y.; Fang D.; Tian Y.; Ding X.; Sun J.; Lookman T.; Xue D. Estimating the performance of a material in its service space via Bayesian active learning: a case study of the damping capacity of Mg alloys. J. Mater. Inf. 2022, 2, 8. http://dx.doi.org/10.20517/jmi.2022.06

About This Article

Copyright

© The Author(s) 2022. Open Access This article is licensed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, sharing, adaptation, distribution and reproduction in any medium or format, for any purpose, even commercially, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Data & Comments

Data

Views

776

Downloads

671

Citations

Comments

Comments

Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.