Recent progress in the data-driven discovery of novel photovoltaic materials
Abstract
The discovery of new photovoltaic materials can facilitate technological progress in clean energy and hence benefit overall societal development. Machine learning (ML) and deep learning (DL) technologies integrated with domain knowledge are revolutionizing the traditional trial-and-error research paradigm that is associated with high costs, inefficiency, and significant human effort. This review provides an overview of the recent progress in the data-driven discovery of novel photovoltaic materials for perovskite, dye-sensitized and organic solar cells. The integral workflow of the ML/DL training progress is briefly introduced, covering data preparation, feature engineering, model building and their applications. The cutting-edge challenges and issues in the ML/DL workflow are summarized specifically for photovoltaic materials. Real examples are emphasized to illustrate how to utilize ML/DL techniques in the discovery of novel photovoltaic materials. The prospects and future directions of the data-driven discovery of novel photovoltaic materials are also provided.
Keywords
INTRODUCTION
Due to their capability to convert clean and inexhaustible solar radiation to electricity directly, photovoltaic technologies, especially solar cells, have provided a new alternative to traditional fossil fuels, which suffer from issues of resource exhaustion and environmental pollution[1, 2]. Though silicon (Si) solar cells have dominated the major commercial photovoltaic markets, as a result of their mature production process, superior stability, and outstanding power conversion efficiency (PCE), the development of Si solar cells has been critically hindered by the high expense of elevated purity Si resources and costly device fabrication[3, 4]. This is evidenced by the continuous decline in their research publications, decreasing from 13% of all solar cell studies in 2013 to 6% in 2022 (until March), as shown in Figure 1A. New photovoltaic technologies are therefore urgently required to replace Si solar cells.
Figure 1. (A) Research trends for various types of solar cells from 2013 to 2022. The percentages in the histograms represent the percentages of each cell in the specific year. We used the search patterns "TS=('solar cell*') AND TS=('perovskite solar cell*')" for PSCs, and "TS=('solar cell*') AND TS=('organic solar cell*')" for OSCs, "TS=('solar cell*') AND TS=('dye-sensitized solar cell*')" for DSSCs and "TS=('solar cell*') AND TS=(Si)" for Si solar cells. (B) Research trends for ML and DL techniques for various solar cells from 2013 to 2022. The numbers in the histograms represent the numbers of references for each cell in the specific year. We added the term "TS=('machine learning' OR 'data mining' OR 'deep learning' OR 'QSPR' OR 'QSAR' OR 'quantitative structure-property relationship' OR 'quantitative structure-activity relationship')" to each search pattern in (A) for the respective solar cell.
There are 3 extraordinary photovoltaic devices in the leading roles of third-generation solar cells, namely, perovskite solar cells (PSCs), dye-sensitized solar cells (DSSCs), and organic solar cells (OSCs), which exhibit their respective potential either in conversion efficiency, stability and/or low production costs, and thus their research contribution in terms of publications has grown from 18% in 2013 to 35% in 2022[5]. In particular, the development of PSCs, after the incubation period of 2009-2014, has been extremely rapid with a significant growth in device performance regarding PCE, from an initial 3.8%[6] to currently over 25.5%[7-10], which is competitive with that of Si-based devices. PSCs have therefore become the veritable superstar in the photovoltaic community and represented 19% in 2021 and even 21% in 2022 of all publications in this field. PSCs illustrate excellent optical and electronic properties, including tunable adjustable bandgaps, long carrier diffusion lengths, high light-absorption coefficients, low nonradiative loss, carrier mobility, and solution processability[11-13]. Despite their promising device performance, significant progress for PSCs is still required towards commercialization due to their low stability, reduced scalability, and potential environmental pollution caused by the use of lead in their chemical composition.
As the nominal parents of PSCs, DSSCs have drawn significant attention since their first report 30 years ago[14], with the merits of relatively low cost, eco-friendliness, structural flexibility, and good stability[15]. Compared to PSCs, DSSCs are much easier to scale up but have struggled with the persistent bottleneck of the relatively lower PCEs of
In recent decades, tremendous experimental efforts have been dedicated to the fabrication and characterization of new photovoltaic materials for solar cells. Most approaches, however, are traditional trial-and-error methods based on expert experience and intuition, along with large costs in terms of time and human endeavor[24, 25]. Computations, especially density functional theory (DFT)[26, 27] -based calculations and molecular dynamics (MD)[28], have been exerted to accelerate experimental investigations and explore the relevant mechanisms behind experimentally observed behavior. Nonetheless, these quantum-based methods are largely restrained by contemporary computing powers that are not well qualified for large-scale simulations with satisfactory accuracy[29]. Like experiments and high-throughput experiments, computations and high-throughput computations also generate huge amounts of data. The data-driven machine learning (ML) and deep learning (DL) methods, as subfields of artificial intelligence (AI), are being quickly adopted by the materials community to fully utilize experimental and computational data to yield a new interdisciplinary field of materials informatics. Materials informatics has already achieved significant success in many branches of materials, such as electrocatalysis, batteries, metal-organic frameworks, two-dimensional (2D) materials, polymers, metals, alloys, and so on[30-33]. Data-driven ML and DL technologies have advantages in catching up the relations between targeted properties and input variables[34]. Coherently integrating the data-driven approach with domain knowledge will make the black box more transparent, enhance ML and DL technologies more efficiently and boost the quantum jump from data to knowledge, thereby paving the way for novel materials discovery[35].
Materials informatics is developing extremely fast in various material fields, including photovoltaic materials. The total number of ML/DL-related studies of solar cells in 2021 was over 180, nearly nine times the number of 19 in 2015 and 50 times that of a decade ago, thereby evidencing the flourishing developing trend in this interdisciplinarity area. As shown in Figure 1B, the main contribution to this fast development is credited to the ML/DL research on PSCs, in which the number of publications increased from six in 2018 to 43 in 2021. The same trend can be observed in OSCs, whose explosive growth was centered in 2019-2021. The related studies on DSSCs show a relatively steady development, with an annual publication number of three to seven. Considering the momentary development of materials informatics in photovoltaic materials and the hundreds of pioneering achievements to accelerate the discovery of photovoltaic materials, it is necessary and timely to review the progress of materials informatics in photovoltaic materials.
In this review, we focus on the recent applications of data-driven methods in the photovoltaic materials of PSCs, DSSCs, and OSCs. We first portray the integral workflow of ML and DL in section "MACHINE LEARNING AND DEEP LEARNING WORKFLOW" (section 2), emphasizing their essential operations in different stages from the preparation of data towards the evaluation of ML/DL models. Real cases are then illustrated in section "RECENT PROGRESS OF DATA-DRIVEN METHODS" (section 3) as examples to show how ML/DL technologies can be used to discover novel photovoltaic materials. The final section addresses the prospects and future directions of material informatics in photovoltaic materials.
MACHINE LEARNING AND DEEP LEARNING WORKFLOW
Figure 2 shows the adaptive design workflow of ML/DL, where domain knowledge, i.e., expert professional knowledge, is the hub. ML/DL work on data, and thus data preparation is the essential and fundamental step. Data are composited by input variables, known as features in ML/DL, and output variables, which are materials properties or other materials characteristics of interest. Features and feature space are two crucial issues in ML/DL, and thus feature engineering must be conducted, which involves the preprocessing, filtering, and generating of features. After that, ML/DL models are developed with ML/DL algorithms. Based on the ML/DL models, recommendations are given to guide the next experiments and/or calculations. The results of the experiments and/or calculations are then put into a database, which iteratively grows until reaching the design goal.
Figure 2. Diagram of ML/DL workflow. RFE/RFA: Recursive feature elimination/addition; GA: generic algorithm; SFE: sequential feature elimination; mRMR: maximum relevance minimum redundancy; SBS: sequential backward selection; SFS: sequential forward selection;
Data collection
The goal of the data-driven procedure is to find the underlying correlations between the target properties and input features via ML/DL algorithms. To avoid "garbage in garbage out" in ML/DL practitioners, a reasonable dataset matters more than the data-driven algorithms, suggesting that more efforts are demanded to cleanse and filter the original dataset[36-38].
Qualified datasets
A reasonable dataset is determined by its data quality, namely, the veracity of each sample, which correlates the portions of inconsistent, incorrect, and missing data. Inconsistent data refer to samples with the same chemical composition, structures, and the same processing conditions but that exhibit diverse values of their target, in which their mean value can be filled if the difference of the diverse values is acceptable[39]. In the converse case, part of the inconsistent data can be presumed based on domain knowledge and/or statistical analysis as the incorrect data, i.e., the outliers. Besides the simple principle "obey the majority", statistical criteria/methods, like the standard deviation, Student's
In the LOF method, the density of neighboring samples for every one of the data is calculated, and the outliers are defined by the ones with their neighbor density lower than a preset threshold. The iForest method builds up a set of decision trees and evaluates the average depth of each sample. Due to the diverse feature values from the normal ones, the outliers are probably isolated at the terminal nodes close to the root of a tree and hence can be defined by the leaf depth smaller than a pre-defined threshold. The MCD method utilizes the Mahalanobis distance based on the covariance matrix of the dataset to evaluate each sample and defines the outliers by the Mahalanobis distance larger than a designated value. In the ABOD method, each sample corresponding to one point in feature space is evaluated by the variance of the angles between vectors from it to every one of the other points. The angles of a normal point in a cluster tend to differ widely and exhibit a relatively larger variance, while an outlier owns the integrally small angle and can be defined by the variance lower than a prefixed cutoff value. The details of these four algorithms are given in Section S1, Tables S2 and S3, and Figures S1 and S2 of the supporting information, along with the code application on how to perform a fast search for outliers. Regarding the missing values of some descriptors, we might drop the sample or descriptor that contains one or more missing values, or fill in the average values, while some cutting-edge ML algorithms, for example, extreme gradient boosting (XGBoost)[50] and categorical boosting (CatBoost)[51], can handle the missing values internally.
Data sources
Databases
Generally, a dataset can be collected from three sources: currently available databases, publications, and lab-scale data. There are several publicly available experimental and computational databases, covering numeric (properties and processing conditions) and image [X-ray diffraction (XRD) and X-ray photoelectron spectroscopy (XPS)] data, such as those listed in Table 1, including the Materials Project[52], Inorganic Crystal Structure Database (ICSD)[53], Open Quantum Materials Database (OQMD)[54, 55], Materials Platform for Data Science (MPDS)[56], Materials Genome Engineering Databases (MGED)[57], Materials Data Specification (MDS)[58] and others[58-62].
Popular online databases
| Database | Link |
| Materials project[52] | https://materialsproject.org/ |
| Inorganic crystal structure database (ICSD)[53] | https://www.psds.ac.uk/icsd |
| Open quantum materials database (OQMD)[54, 55] | https://oqmd.org/ |
| Materials platform for data science (MPDS)[56] | https://mpds.io/ |
| Materials data specification (MDS)[58] | https://github.com/conchsk/Materials-Data-Specification |
| Automatic-flow for materials discovery (AFLOWLIB) | http://aflowlib.org |
| American mineralogist crystal structure database | http://rruff.geo.arizona.edu/AMS/amcsd.php |
| Cambridge crystallographic data center (CCDC)[61] | www.ccdc.cam.ac.uk/pages/Home.aspx |
| Chemspider | www.chemspider.com |
| Computational materials repository (CMR) | http://cmr.fysik.dtu.dk/ |
| Crystallography open database (COD)[62] | www.crystallography.net |
| Database of materials properties (MatDat) | www.matdat.com |
| NIMS materials database (MatNavi) | https://mits.nims.go.jp/ |
| NanoHUB | https://nanohub.org/ |
| Total materia | www.totalmateria.com |
| Pauling file | http://paulingfile.com |
| PubChem | https://pubchem.ncbi.nlm.nih.gov/ |
| Materials genome engineering databases (MGED)[57] | https://www.mgedata.cn/ |
Significant time can be saved by building ML models using databases instead of collecting samples from publications. As a result, researchers can instead dedicate their efforts to selecting, comparing and cascading the ML algorithms. For instance, Rafael et al.[63] proposed an automatic chemical design approach by combining the variational autoencoder (VAE) framework and the open-source cheminformatics suite RDKit[64]. Two autoencoder systems were carefully designed and fitted based on one dataset with 108, 000 molecules from QM9[65] and another dataset with 250, 000 drug-like commercially available molecules extracted at random from ZINC[66]. The most publicly available databases usually contain general information without specific properties and processing conditions. For example, it is difficult to obtain PCE data from the OQMD database. In this context, databases for specific types of materials might be more important for their particular fields[31]. The Harvard Clean Energy Project (CEP) is a distributed computing effort for screening organic photovoltaic candidates carried out by volunteers connected to the IBM World Community Grid[67], which has provided 1.3 million donor materials for non-fullerene materials[68]. The NIMS Materials Database (MatNavi) aims to contribute to the development of new materials and the selection of materials, and covers polymers, inorganics, metallics and their computational properties. The Harvard Organic Photovoltaic Dataset (HOPV15) is formed on the CEP and has assembled experimental photovoltaic structures from the literature along with their quantum-chemical calculations performed over a range of conformers[69]. Venkatraman et al. constructed the DSSCDB (DSSC database) to provide over 4000 synthesized sensitizer dyes with the reported device details, such as performance and experimental processing conditions[70].
Publication data
Collecting data from publications is the second choice, especially when there is a lack of accomplished, authoritative, and professional databases in the concerned fields. Odabası et al. presented an overview and analysis of the 1921 organo-lead-halide PSC device performances that were accumulated from 800 publications between 2013 and 2018[71]. By extending the dimensions of the dataset, more assessments on the reproducibility, hysteresis, and stability of the extended dataset using association rule mining methods were further carried out in 2020[72, 73] and 2021[74]. Compared to the direct usage of databases, it is noteworthy that significantly more endeavors are urgently required to check the consistency and integrity of the collected data before ML/DL model building.
Lab-scale data
Lab-scale experiments and computations in individual research labs are the most fundamental and widely distributed data sources and generate original and valuable data. Coinciding with the developments in high-throughput experiments and computations, the scale of data is growing fast, especially the size of calculated data, which are scaled up quickly through high-throughput platforms and various quantum-based software like Materials Studio (MS) [75], the Vienna Ab initio Simulation Package (VASP)[76-79] and the Gaussian suite[80]. In the work of Hartono et al., 21 organic salts were deposited as capping-layer materials on the top of a thick film of methylammonium lead iodide (MAPbI
Descriptor generation
Descriptors, also known as features, and search space are the two crucial issues in ML. The descriptor types of material structures depend on whether the structures are aperiodic or periodic. Aperiodic structures can be stored in the file types of the simplified molecular-input line-entry system (SMILES) or molecular file (MOL), while periodic ones can be dumped into crystallographic information files (CIFs). Aperiodic system structures, including the pure organic structures of photovoltaic absorbers in OSCs, DSSCs, and metal-organic frameworks (MOF), can be depicted using molecular descriptors, while atomic and crystal structural descriptors are generally used for periodic systems, e.g., the crystal perovskite structures in PSCs.
Molecular descriptors
Thousands of molecular descriptors in dozens of types have been proposed and generated with assorted tools[85]. Taking one of these tools, Dragon software[86, 87], as an example, we can generate 5270 descriptors in 30 types [Table S1], from the simplest 0-dimensional (0D) constitutional indices to the most abstract and complicated 3-dimensional (3D) spatial representations. The optimized structures via DFT calculations are needed for the generation of 3D descriptors, while the other descriptors can be based on only 2D structures, such as in the SMILE format and its enhanced versions, such as Selfies[88].
The development of an interpretable ML model requires simple and understandable descriptors, e.g., the descriptors marked as "Easy" in Table S1. Kar and co-workers[89] generated, using Dragon 6 software, 248 simple descriptors covering constitutional indices, ring descriptors, topological indices, connectivity indices, functional group counts, atom-type E-state indices, and 3D-atom pairs from the optimized structures for 273 collected arylamine organic dyes that were divided into 11 groups. Eleven linear regression models with interpretative features were then developed to predict PCE values with robust performances, and 29 new materials were accordingly designed with higher predicted PCE values. In 2020, Krishna et al.[90] collected over 1200 dyes from seven classes and generated only 2D descriptors from Dragon 7[86] and PaDEL-descriptor 2.21 software[91]. Eight linear models targeting the PCEs for each structure type were built along with their detailed feature interpretations, while ten new materials were designed with better predicted target values. Our group also has conducted relevant studies, especially on the interpretation of more abstract descriptors[92, 93]. In our work[92, 93], 3 hardly interpretable descriptors were successfully unveiled in the relations between the structures of sensitizers and their PCE values, as illustrated in Section S2, where Mor14p and Mor24m could be explained in favor of C
Fingerprints (FPs), as defined by Shemetulskis et al., are the fixed size Boolean vectors that encode molecules by exploding their structures in all the possible substructure patterns under a given set of rules[94]. The most widely-used types are the path-based FPs that represent the substructures as linear chains of connected atoms and the extended connectivity fingerprints (ECFP) that use a variant of Morgan's extended connectivity algorithm[94-97].
FPs were originally introduced for fast database searching by evaluating the similarity/diversity between compounds. In recent years, FPs have been integrated into tools like Dragon software[86] and RDKit[64] and also applied in ML models for various organic systems, such as sensitizers in OSCs and DSSCs. Sun et al. used FPs, images, SMILE strings, and structural descriptors to depict the structures of 1719 organic photovoltaic donor materials collected from publications[98]. The random forest (RF) model with FPs achieved the highest accuracy of 86.67% in the classification task to identify the binary categories with a 10% PCE as the boundary. Kranthiraja et al. generated ECFPs for a collection of 556 samples of organic photovoltaic materials[99]. A RF model targeting PCEs was trained to yield a correlation coefficient (
Atomic descriptors
Compared to organic materials, periodic systems are dependent on their atomic and crystal structural descriptors. Atomic descriptors are publicly accessible in the Mendeleev package[100], Villars database[56], and RDKit[64], while structural descriptors are extracted from quantum-optimized crystal structures. Li et al.[101] employed the Python Materials Genomics (pymatgen) package[102] to obtain the atomic information and crystal structural parameters for 1593 ABO
In addition to the public resources mentioned above, one very early work accomplished by Chen[104] also investigated the atomic descriptors (also described as the atomic parameters or parametric functions of chemical bonds) covering ionic radius, covalent radius, ionization energy, metal radius, ratio of valence electron to covalent radius, electronegativity, and equivalent conductance, as shown in Table 2. Chen not only assembled the bond parameters from the works of Slater[105], Belov[106], Pauling[107], Quill[108], Zachariasen[109], Sanderson[110], and Goldschmidt[111], but also reproduced and complemented the results with quantum calculations. The details of the atomic parameters have been extracted from Chen's work and provided in Section S3, which have been utilized in ML[112].
Bond parameters arranged by Nianyi Chen
| Bond parameter | Description |
| Ionic radius [Table S4] | Ionic radii for elements sand some chemical fragments |
| Covalent radius [Table S5] | Covalent radii for elements |
| Ionization energy [Table S6] | Ionization energies for elements along with different degrees from Ⅰ to Ⅷ |
| Metal radius [Table S7] | Metal radii of the metal atoms in their elemental metal |
| Valence electron to covalent radius ratio [Table S8] | The ratio of covalent radius [Table S9] divided by valence electron number |
| Electronegativity [Table S9] | Electronegativity for elements |
| Equivalent conductance [Table S10] | Equivalent conductance for molten chloride when the materials are at their melting point |
Such atomic descriptors might not be compatible with hybrid organic-inorganic perovskite (HOIP) structures due to the lack of relevant organic molecule properties for the A site (considering the HOIP chemical formula of ABX
Other forms of representation
In addition to the descriptors discussed above, images are also one of the promising media to represent structures. Sun et al. fed a deep neural network with the images of chemical structures to classify the performances of organic solar cells with an accuracy of 91.02%[117]. Other image data from, for example, XRD and XPS, may also have the potential to represent structures, but few publications have been reported so far.
3D atomic coordinates can also be utilized as input values directly. The graph convolutional neural network (GCNN) is a new framework in deep learning for representing periodic crystal systems that are usually based on the coordinates in quantum-based optimized structures[118, 119]. The GCNN treats the input crystal structures as a relational graph in which each atom is viewed as a node, and the connection relation between atoms is regarded as an edge. The model learns and updates the node and edge information in the crystal graph and finally deduces the relations between the coordinates and the output. Xie et al.[120] trained a GCNN model to predict various quantum-based properties of crystal structures extracted from the Materials Project[52], achieving mean absolute errors of 0.004-0.018 log(GPa) for the bulk/shear moduli and 0.097-0.212 eV for the formation energy and bandgap.
Another method to improve the information quality of features is to utilize symbolic methods that can generate a massive set of descriptors using combinations of the algebraic functions applied to existing features by relevant tools such as gplearn[121], DEAP[122] and the sure independence screening and sparsifying operator (SISSO)[123]. For instance, Bartel et al. successfully discovered an improved tolerance factor for the formability prediction of perovskites using the SISSO[124].
Data preprocessing
The collected data must be preprocessed to check their consistency and noise, especially for the same experimental data with the same testing conditions reported by different researchers. In addition, string variables that contain not just numbers but also other alphabetic characters (typically represented as categorical variables, e.g., lattice structures of hexagonal, tetragonal and cubic) are usually coded into integers by applying coding algorithms such as the one-hot encoder. If 2 variables are highly correlated, one of them should be removed to reduce the redundancy.
Scaling data is one of the prerequisite steps in data preprocessing to transform the input values into the same range, e.g., 0 to 1, which is optional for the tree-based algorithms that are insensitive to variable ranges. Several common scaling methods are accessible in the Python package scikit-learn (sklearn)[125]. For example, the standardization method is the most widely used and transforms data to the center with a zero mean and unit variance. Min-max scaling transforms the variables to lie between a given minimum and maximum value, often between 0 and 1.
The third important preprocessing step is to randomly divide a whole dataset into three subsets, usually by arranging a training set for building models, a validating set for evaluation while tuning model hyperparameters, and a test set for final evaluation of the model predicting performance. If the whole dataset is sufficiently large, the three subsets should possess the same distributions as the whole dataset[126, 127]. However, the random splitting method does not operate well in relatively smaller and/or sparsely populated data, and hence the trained model tends to misjudge the test samples. Thus, when encountering a small dataset, the K-fold cross validation (K-CV) can be used to replace the validation set. In the K-CV method, the sample sets are randomly divided into K folds, with one of the folds used as the validating set and the rest of the folds acting as the training set. The divided training and validating sets are conducted K-times such that each of the K-fold data is used as a validating set once, and the average performances of the K models are taken as the trained ML model. If the fold number K is equivalent to the number of samples, then each fold contains only one of the samples and the method is deemed LOOCV.
Feature selection
The next crucial step is the feature selection to determine the critical features highly related to the target values and eliminate the redundant variables. Generally, feature selection methods can be classified into three types, namely, filter, wrapper, and embedded methods[128].
Filter-type methods evaluate variables that only rely on the general characteristics of the dataset and do not involve any ML algorithm, which is advantageous for low computing costs[38, 129]. For instance, the minimum redundancy maximum relevance method (mRMR)[130-132] selects the optimal features by inspecting the relevance between the features and the target, and the redundancy among features. The maximum relevance is revealed by searching for the features that have the largest mutual information to the target
where
The redundant information among the features in
where
Therefore, we can combine Equations (1) and (3) and consider the following simplest form to optimize them simultaneously:
Using Equation (5), Gallego et al.[132] gave one of the simplest algorithms as follows:
(1) Select one feature.
(2) Calculate its mutual information with the target as the relevance.
(3) Calculate its mean mutual information with other features as the redundance.
(4) Determine the difference between the relevance and redundancy as the mRMR score.
(5) Rank the features based on score.
After ranking the features by mRMR scores, one might propose a threshold and select features where the mRMR scores are higher than the threshold. Furthermore, mRMR scores can be combined with an ML model to select features. For example, based on the features ranked by the mRMR score, the recursive feature addition (RFA)[133] procedure can be used to determine the best feature subset by adding or removing one or more features, as follows:
(1) Select the top feature in the ranked features.
(2) Train and evaluate an ML model.
(3) Select the top two features in the ranked features to evaluate the new model.
(4) Subsequently, select the top three, four, five, and so on features in the ranked features and evaluate the new model, which results in the optimal feature subset with the best model performance.
The opposite recursive feature elimination (RFE) performs the same procedure but starts from the full feature set and eliminates features from the inverse order. By combining the mRMR filter method and the RFA/RFE procedure, an optimal feature subset for the model construction can be obtained, while the mRMR can be alternated by other filter methods, such as the variance threshold, mutual information, and chi-squared test methods[128].
Differentiating from filter types, wrapper methods select features depending on the model performance of an ML algorithm and typically iteratively repeat two steps: (1) searching for a feature subset; (2) evaluating the model performance with the feature subset, with the best performance corresponding to an optimal feature subset. In the typical representative genetic algorithm (GA)[122, 134-137] method, each feature subset is regarded as a chromosome and has its own fitness that refers to the model performance of a specified algorithm. The superior/inferior chromosomes are retained/discarded, while new chromosomes are regenerated in each iterative step (known as generation) by mutating and crossing over. The detailed procedure of a GA is as follows:
(1) Generate a population composed of chromosomes. Each chromosome represents a feature subset.
(2) Evaluate chromosomes in this population by an ML model with a loss function. The model performance is set as the score for each chromosome.
(3) Deprecate the chromosomes with low scores.
(4) Crossover a randomly selected pair of chromosomes by exchanging their subparts to generate two new chromosomes and supplement the population.
(5) Mutate a randomly selected chromosome (usually
(6) Repeat steps (2)-(5) until the maximum step is reached.
Another widely used wrapper type is sequential forward selection (SFS) and its backward counterpart (SBS)[138]. SFS starts with one feature and finds the best feature that can maximize the performance of a model trained by one feature only, where, in contrast to RFA, every one feature is chosen randomly or iteratively. The second feature (every feature is chosen randomly in the rest features) is then added, the model is trained by two features, and the best second feature is selected. The procedure continues until the best performance is found by testing, which finally selects the desired features. SBS follows the same concept but from the full feature set and removes one feature that can maximize the model performance.
Embedded methods perform the feature selection in the process of training ML models and are specific to some ML algorithms that can export feature scores internally, e.g., tree-based algorithms (decision trees, RFs, and so on)[129, 139]. When constructing a decision tree structure, the change in the Gini index caused by each feature is calculated and the features with high influence on the Gini index can be chosen for the selected set to train the decision tree model[140]. In addition, in the RF algorithm, multiple decision tree models are combined together, and the important features are determined by the average entropies from the sub-trees. In this regard, the features are sorted by Gini entropies in tree models and the feature subset is then selected via the RFA or RFE procedure. For example, Wen et al. employed embedded methods by combining RFE and tree-based models to select the features, which led to up to nine features remaining[141]. Li et al. adopted the same method to filter the optimal instrumental features for the bandgap of ABO
The contributions of features to model predictions can be evaluated by SHAP values[82, 142] Given a full feature set
where
ML model construction
We now consider the core stage to select a suitable data-driven model for describing the relationship between the features and properties comprehensively, which also can be regarded as establishing a mapping function with multiple inputs and one or multiple outputs using ML/DL techniques. Benefitting from the decades of efforts taken by scientists in the fields of computer science, mathematics, and other related fields, abundant choices of user-friendly ML/DL algorithms [Table 3] with powerful predictivity have been publicly distributed and widely used, involving the typical tools, such as sklearn[125], XGBoost[50], LightGBM[144], PyTorch[145], and TensorFlow[146], which help materials scientists focus on exploiting feature spaces.
Popular ML/DL algorithms for materials design
| Algorithm Category | Derived Algorithm | ML Task Type | Comment/Trait |
| Linear model | Linear regression (LR) | Regression | Traditional but still widely used |
| Logistic regression classification (LRC)[154-156] | Classification | Introduce logistic function into LR | |
| Lasso regression[158, 159] | Regression | Introduce L1 regularization penalty into LR | |
| Ridge regression (RR)[160] | Regression | Introduce L2 regularization penalty into LR | |
| Decision tree | Iterative Dichotomiser 3 (ID3)[222] | Classification | Use entropy to build decision tree |
| C4.5[223] | Classification | Use entropy gain ratio to build decision tree | |
| Classification and Regression Tree (CART) [164] | Regression and classification | Use Gini entropy to build decision tree. Usually, the term of decision tree refers to CART algorithm | |
| Ensemble trees (Averaging approach) | Pasting[167] | Regression and classification | Multiple trees are parallelly trained on randomized sample subsets without replacement |
| Bagging[168] | Regression and classification | Multiple trees are parallelly trained on randomized sample subsets with replacement | |
| Random subspaces[169] | Regression and classification | Multiple trees are parallelly trained on randomized feature subsets with replacement | |
| Random forest (RF)[170] | Regression and classification | Multiple trees are parallelly trained on randomized samples and feature subsets with replacement | |
| Ensemble trees (Boosting approach) | Adaboost[172] | Regression and classification | Multiple trees are sequentially trained to optimize sample weights |
| Gradient boosting machine (GBM) [173] | Regression and classification | Multiple trees are sequentially trained to eliminate the bias of previous trees | |
| XGBoost[50] | Regression and classification | Introduce second-order Taylor approximation and L2 regularization into GBM | |
| Light gradient boosting machine (LightGBM) [174] | Regression and classification | Introduce gradient-based one-side sampling and exclusive feature bundling to GBM | |
| CatBoost[51, 175] | Regression and classification | Adopt ordering principle into GBM | |
| Support vector machine (SVM) [48, 177, 178] | Support vector regression (SVR) | Regression | A "must-try" and widely used algorithm. SVM usually has robust performance in most ML tasks |
| Support vector classification (SVC) | Classification | ||
| Gaussian process (GP) [180, 181] | Gaussian process regression (GPR) | Regression | GP develops from Bayesian theorem, and has few parameters to be adjusted |
| Gaussian process classification (GPC) | Classification | ||
| Deep learning | Artificial neural networks (ANN) | Regression and classification | Composed of dense layers |
| Suitable for 2-dimensional data | |||
| Convolutional neural network (CNN) | Regression and classification | Used for image data | |
| Graph convolutional neural network (GCNN) [38] | Regression and classification | Used for coordinates data | |
| Recurrent neural network (RNN)[184] | Regression and classification | Used for sequential data | |
| Long short-term memory (LSTM) network [184] | Regression and classification | Used for sequential data | |
| Gate recurrent unit network[184] | Regression and classification | Used for sequential data | |
| Generative adversarial network (GAN) [185-187] | Regression and classification | Consist of an unsupervised generator model and a supervised discriminator model, aiming to produce promising candidates for inverse design | |
| Variational autoencoder (VAE)[188] | Regression and classification | Involve an encoder network and a decoder network, and build latent space to represent material structures |
ML algorithms
Linear model
Linear regression. One traditional but still widely used algorithm is linear regression (LR), which expects the target value to be a linear combination of the features. A linear model is usually fitted by reducing the residual sum of squares between the observed and approximate target values via the ordinary least square method. In spite of its simplicity, there are still a large number of applications in photovoltaic fields[89, 90, 92, 147-149]. For example, in the works of Kar[89, 90, 150-153], the LR algorithm was largely employed to fit multiple robust linear models for DSSCs.
Logistic regression classification. Logistic regression classification (LRC) is proposed to complement the classification form of LR by introducing a logistic function to predict the probability of a certain label[154-156]. Yu et al. built up an LRC model to determine whether a perovskite film exists after post-treatment, which led to a competitive test accuracy of 84% to 86% of the SVM[157].
Lasso and ridge regression. To reduce the overfitting problem of LR, the L1 regularization penalty is imposed into the calculation for the residual sum to form the lasso regression[158, 159], while the L2 regularization penalty is expected to obtain the ridge regression (RR) [160]. In the work of Li et al., the lasso model, which was fitted to predict the formation energy of hypothetical perovskite materials based on only composition and stoichiometry information, exhibited a 10-fold cross-validation
Decision trees
The so-called classification and regression tree (CART) algorithms, also known as decision trees, construct a tree-like structure by a binary recursive partitioning procedure capable of processing continuous and categorical features. The data samples are partitioned recursively into the binary nodes in each step (known as depth) by making a decision based on feature attributes until the number reduces to zero or the depth reaches a specified maximum[164]. Given the naive operating rule, it is simple to understand and interpret CART models by visualizing their tree structures. For example, Paul et al. trained a decision tree model for inorganic-organic hybrid materials to gain more deep insights into the influence of experimental conditions and perovskite properties on the reaction outcomes[165].
Ensemble methods
Ensemble methods have gained significant popularity in recent years due to their merits of robustness, stability, and generalization[38, 166], which particularly refers to the tree-based mathematic approaches of assembling multiple CART models to promote the performance over a singular tree model.
Averaging approach. One common case in ensemble methods is the averaging approach, which leverages the outputs from the several parallelly and independently fitted CART models on average. The base models might be trained on different training sets that are sampled from the whole dataset. When the random sample subsets are drawn for each CART model, the algorithm is called pasting[167]. When the random sample or feature subsets are drawn with replacement, the method is known as bagging[168] or random subspaces[169]. If the random sample and feature subsets are both drawn with replacement, the method is entitled RF[170]. The base models are organized together and make a collective decision, in which the sklearn package provides the basic module "Voting Class" that is convenient to fill any other model rather than the CART model. Takahashi et al. trained a RF model to predict bandgaps of perovskite materials and estimated 9328 candidates, where 11 undiscovered Li-/Na-based structures had an ideal bandgap and formation energy for solar cell applications[171].
Boosting approach. Another case in ensemble methods is the boosting approach. The critical idea here is to build a series of CART models in sequence, with each model fitted to reduce the whole bias from the former assembled CART models. The final outputs of the boosting model are then determined by the whole sequentially fitted CART models. Adaboost was the first proposed boosting algorithm whose trait is to repeatedly modify the sample weights in each step of building a new CART model, in which the weights of the samples with large predicted errors are enhanced and each new CART model is trained on the reweighted samples[172]. The most prevailing algorithm under the boosting theory is GBM and its derivatives, also known as gradient boosting trees (GBTs) [173]. Rather than modifying sample weights, each CART model in GBM is trained to predict the bias resulted from the whole former models and the finial outputs are the sum of the whole model predictions. The derivatives aim to reduce the computing cost and promote the fitness of GBM. XGBoost is proposed by imposing a second-order Taylor approximation and L2 regularization into the loss function, which can simplify the procedure of building each CART model[50]. The light gradient boosting machine (LightGBM) introduces gradient-based one-side sampling and exclusive feature bundling to largely reduce the sample numbers and the feature dimensions to lower the computing and memory costs when dealing with gigantic data[174]. CatBoost adopts an ordering principle to handle the specified cases that contain a large number of categorical features[51, 175]. Sahu et al. employed RF and GBM models to predict the OSC device performance based on 13 material descriptors, giving the similar cross-validation results for PCE values with
Support vector machine
SVMs, including support vector classification (SVC) and support vector regression (SVR), are also some of the most widely-used algorithms and have become a must-try method because of their robust performance and fast computing efficiency[48, 177, 178]. With a kernel function, SVC finds a separating hyperplane with the maximum margin in a high-dimensional space, while SVR regresses responses and features in a high-dimensional space and tolerates error
Gaussian processes
Gaussian processes (GPs) for ML are developed based on the Bayesian theorem and Gaussian probability distribution[180, 181]. Unlike in other deterministic ML regressions, GP regression utilizes the Gaussian probability distribution to regress data and express regression results in terms of mean and covariance of the maximal posterior distribution. The following are the responses
where
Clearly, the predication of
The prediction follows the normal distribution
where
Deep learning
Artificial neural network. The term deep learning (DL) refers to miscellaneous architectures of neural networks. The artificial neural network (ANN) or multi-layer perceptron has the simplest and most understandable structure, whose structural units comprise the fully connected layers (known as dense layers). As shown in Figure 3A, a deep ANN model is composed of multiple dense layers with a conic distribution in layer length. The input data, starting from the input layer, are processed through all the dense layers by multiplying each parametric weight matrix in each layer, which is finally output as the predicted value. A typical example can be found in the work of Li et al., in which the trained ANN model for PSCs achieved the best performance against the other ML models with the highest
Convolutional neural network. By appending convolution layers in front of the dense structure, as shown in Figure 3B, the convolutional neural network (CNN) is formed to extract spatial features from images, which can be applied in processing characteristic results that are presented as images, such as from XRD, XPS, and so on[38]. As mentioned in the descriptor section, the GCNN is suitable for convolving spatial structure information from coordinate data and has been applied in predicting the moduli, formation energy, and bandgap of crystal structures from the Materials Project[52] by Xie et al.[120].
Recurrent neural network. Other advanced DL architectures may also have significant potential for materials science applications, though there have been few reported publications. For example, when dealing with sequential data, including various spectra data, the recurrent neural network (RNN), long short-term memory (LSTM) network, and gate recurrent unit network can be exerted to train the relevant model[184].
Generative adversarial network. The generative adversarial network (GAN)[185-187] is a sophisticated DL architecture consisting of an unsupervised generator model and a supervised discriminator model, which aims to produce promising candidates for inverse design[184] Specifically, the goal of a generator model is to fit a function
Variational autoencoder. The variational autoencoder (VAE)[188] is a comparable DL architecture to GAN involving an encoder network and a decoder network, whose novelty is to build a so-called latent space to represent the material structures[63] Crucially, the encoder network maps the material structures (in the SMILE or CIF format) to vectors in a lower-dimensional space known as latent space, which acts to compress the information from the original data into the vector in latent space. Furthermore, the decoder network performs the inverse operations to decompress the vector to its original form. By training both the encoder and decoder networks to process and reproduce the original data, the VAE model is expected to learn the potential features from the real data samples. Benefitting from the continuous and differentiable vectors in latent space, we can extrapolate and construct new reliable material structures by applying direct search engines (e.g., greedy search), since latent space is a continuous vector space.
Evaluation metrics
Before an ML/DL model is trained, as discussed in section "Data preprocessing" (section 2.3), a dataset is usually divided into a training set, validating set, and test set. The prediction of a trained model on the training set is referred to as the training prediction and the relevant metrics are known as the training metrics. The training metrics usually reveal good performance since the samples are already used in training and therefore cannot be an effective indicator for the model performance. Similarly, the validating and test predictions and metrics can be obtained when predicting the samples in the validating and test sets. Good validating metrics are adopted to optimize the hyperparameters, if any. High performance in test metrics signifies excellent predictivity and generalization abilities.
In regression, the determination coefficient (
The Pearson correlation coefficient (
The values of
Various prediction errors can be adopted to signal the model predicting error. For example, the mean absolute error (MAE) is the mean of the absolute difference between each observation and prediction. The mean squared error (MSE) is calculated from the mean of the squared difference. The root mean squaref are the correctly predicted while the off-diagonal elemen error (RMSE) is the root of the MSE. The value ranges of error metrics are largely dependent on the target range.
In the classification task, the total accuracy can be used to indicate the performance of classification models, which is the division between the correctly predicted samples and the whole samples. To gain more detail, the confusion matrix, also known as the error matrix, can be employed, which is an N-square array (N is the categorical number of labels), as shown in Figure 4A. The columns represent the observed labels and the rows indicate the predicted labels (the definitions of the two axes can be swapped). The element in each pixel expresses how many samples belonging to the observed label are estimated as the predicted label. Apparently, the diagonal elements are correctly predicted, while the off-diagonal elements are all incorrect. The accuracies of a specified class can be obtained by dividing the specified diagonal element by the sum of the corresponding row. With regards to the binary classification that contains the positive or negative labels, as shown in Figure 4B, the correctly predicted positive samples are deemed true positive (TP), while the correctly predicted negative, incorrectly predicted positive and incorrectly predicted negative samples are referred as true negative (TN), false positive (FP), and false negative (FN), respectively. Precision is defined as the accuracy of the positive samples, while the recall score refers to the division of TP over the sum of TP and FP, representing the ability of the classification to find the positive samples with the best value of 1. The F1 score is the combination of the precision and recall score, defined as:
Figure 4. Classification task for (a) multiple and (b) binary labels. TP: True positive; TN : true negative; FP: false positive; FN: false negative.
The F1 score is interpreted as a weighted average of the precision and recall score, whose best value reaches 1 and the worst is 0.
In a clustering task, the Silhouette coefficient (SC) is the most common indicator, which is calculated as[189]:
where
Hyperparameter optimization
Each algorithm might have its own hyperparameters that cannot be directly trained in the training process, such as a penalty factor, kernel function for SVM, CART tree number, learning rate for GBM, and so on. The hyperparameters need to be optimized to gain the best set of hyperparameters for a specified model. The grid search (GS) approach combined with K-CV is the most common method, and it exhaustively exploits the whole hyperparameter search space to find the globally optimal parameter set, which is effective for a discrete search space consisting of only a few hyperparameters but is unacceptable regarding time and computational cost for a uniform search space with multiple dimensions. Due to its simplicity, GS has been widely employed in current publications. Hartono et al. optimized the KNN, RF, GBM, ANN, and SVM models using the GS approach from the sklearn package[81], while Choudhary et al. utilized the same method to exploit the hyperparameters for the LightGBM model[190].
To overcome the high expense of the GS approach regarding time and computational cost, various alternatives have been proposed. The sequential model-based optimization (SMBO) constructs a surrogate model to approximate the hyperparameter distribution in the hyperparameter space. In SMBO, the hyperparameters and optimized object (e.g., LOO RMSE or CV5 MSE of the ML model) are regarded as the input and output, respectively. The criterion of expected improvement (EI) is usually adopted as the optimized object in the SMBO method, which can be defined as Equation (15):
where
(1) Draw several random points
(2) Fit a GPR surrogate model to approximate
(3) Find and evaluate several sets of optimal hyperparameters in current distribution
(4) Add the pairs of new evaluated points
(5) Repeat steps 3 and 4 until the iteration terminates.
Bergstra et al.[191] proposed a tree-structured Parzen estimator approach to modify the
where
By applying
Equation (18) shows that to maximize
Other useful methods may also have their own merits of automated searching, efficiency, and easy parallelization, such as the Optuna[192] and Ray[193] packages; however, they are beyond the scope of this review.
ML model applications combined with domain knowledge
High-throughput screening
Among the common ML model applications listed in Table 4, high-throughput screening might be the most popular method to apply a fitted model in materials science, which filters potential materials with the required properties that are predicted by the model. To decrease incorrect trials in experiments and accelerate the search procedure more efficiently, domain knowledge may be required not only to restrain the search space for candidate materials as much as possible in pursuit of low costs in time and computation, but also to downselect the optimal candidates from the high-throughput screening results.
Popular ML model applications
| ML model application | Description | Examples |
| ML: Machine learning; GBM: gradient boosting machine; SVR: support vector regression; KRR: kernel ridge regression; ANN: artificial neural network; LED: light-emitting diode; BODIPY: boron-dipyrromethene; PCE: power convention efficiency; | ||
| High-throughput screening | Use a well-fitted model to predict hugepotential materials generated frompermutations. The materials are furtherlyfiltered by domain knowledge and theoptimal candidates are down-selected fromthe large-scale samples. | Wu et al. predicted the bandgaps of 38086 HOIPs using GBM, SVR, and KRR models.686 candidates with bandgaps of 1.5-3.0 eV were selected[179] |
| Lu et al. used three GBM models to predict the structure type, bandgaps and polarizabilities of 19841 ferroelectric photovoltaic materials, resulting in 151 shortlisted candidates[194] | ||
| Gómez-Bombarelli et al. built an ANN model to predict the delayed fluore- scence rate constant of 1.6 million LED molecules, leading to the four most promising ones that were further identified by experiments[197] | ||
| Online ML model | The fitted models could be shared to other researchers on websites. The visitors could obtain the predictions from the online models directly by uploading their own data as the required format. | Lu et al.[93] provided two BODIPY dye models to predict the PCEs at http://materials-data-mining.com/bodipy/ |
| Tao et al.[198] offered one model to predict the bandgaps of perovskite oxides at http://materials-data-mining.com/ocpmdm/material_api/ahfga3d9puqlknig and another model to predict corresponding hydrogen production at http://materials-data-mining.com/ocpmdm/material_api/i0ucuyn3wsd14940 | ||
| Xu et al.[199] afforded their model to predict polymer bandgaps at http://materials-data-mining.com/polymer2019/ | ||
| Model analysis | Critical factors could be identified by calculating feature importance and further analysis to explore the underlying principles between properties and structures. | Xiong et al.[39] identified the vital features |
| Zhang et al. extracted the important features from XGBoost model, including the radius, first ionization and lattice constant of B site, the radius of A site and tolerant factor[143] | ||
| Jin et al. pinpointed the most crucial feature packing factor from GBM model[200] | ||
| Yu et al.[157] obtained the significant features of sigma orbital electronegativity, acceptor site count, Balaban index, donor count and distance degree from lasso model | ||
Wu et al. prepared a search space of 230808 ABX
Lu et al.[194] collected 1102 ferroelectric photovoltaic materials (407 perovskites and 702 non-perovskites) from the literature[195, 196] to build up a classification GBM model to determine the perovskite structure and two regression GBM models to predict the bandgap and polarizability. The search space for the candidates was constructed by the elements involved in the dataset, leading to 19841 potential compounds in total. After being predicted by the three GBM models, 151 ferroelectric photovoltaic perovskites were shortlisted and further evaluated by first-principle calculations.
Gómez-Bombarelli et al. created a search space of over 1.6 million structures to identify promising novel organic light-emitting diode (LED) molecules[197]. An ANN model was trained to predict the delayed fluorescence rate constant. A total of 2500 candidates were filtered with suitable predicted values and further evaluated by human experts on a custom web voting tool. The four best potential candidates voted by the experts were finally synthesized and tested experimentally, with a consistent result with the model predictions found with a mean unsigned error of 0.1
Online ML models
Fitted models can be shared with other researchers by providing them on public websites, and this is an area where significant progress has been achieved in our group. For example, two boron-dipyrromethene (BODIPY) dye models were provided at http://materials-data-mining.com/bodipy/, which are widely accessible to use as established models for predicting the PCE values of BODIPY devices[93]. Tao et al. constructed two models for predicting the bandgap (http://materials-data-mining.com/ocpmdm/material_api/ahfga3d9puqlknig) and hydrogen production rate (http://materials-data-mining.com/ocpmdm/material_api/i0ucuyn3wsd14940) of perovskite oxides[198]. It is only required for the users to provide chemical formulas to predict the bandgap and formulas plus experimental conditions to predict the hydrogen production rate. Xu et al. afforded their model to predict the bandgap of polymers at http://materials-data-mining.com/polymer2019/, along with a full illustration of the ML training procedure[199].
Model analysis
In addition to models predicting applications, analysis based on feature importance can also help to identify critical factors, which can further clarify the underlying principles between the factors and properties by combining our domain knowledge. The SHAP approach is one emerging method for the analysis of feature contributions to model predictions.
In one of our recent works[39], SHAP was employed to explore the feature importance in established RF models that were targeted to hardness and ultimate tensile strength (UTS) for complex concentrated alloys (CCAs), in which the most vital features were identified, covering the valence electron
We also applied SHAP to identify the most important structural factors to predict the formability of HOIP materials[143], in which the XGBoost classification model was built based on 102 HOIP samples and the filtered atomic descriptors along with the LOOCV accuracy of 95% and test accuracy of 88%. According to the SHAP analysis, it was found that the radius and lattice constant of the B site in ABX
In the research of Jin et al., the feature importance from the GBM model was utilized to pinpoint the most crucial feature known as the packing factor[200], while Yu et al. adopted the feature importance from the lasso model to identify the significant features of sigma orbital electronegativity, acceptor site count, Balaban index, donor count and distance degree[157].
RECENT PROGRESS OF DATA-DRIVEN METHODS
Data-driven progress in PSCs
As discussed in the introduction, despite innumerable merits as absorbers in solar cell devices, perovskite materials, especially in the case of HOIPs, still face imperfections regarding scalability, stability, and environmental pollution. Scalability is mostly related to deposition, film formation, and device integration[201, 202], which are beyond the scope of this review. The remaining two issues are mainly attributable to the unstable structures and the incorporation of Pb in HOIPs, e.g., the mostly used MAPbI
Typical ML publications of PSCs
| Publication | Sample | Feature | ML Task | ML Algorithm | (Best) Model Performance |
| ML: Machine learning; PSCs: perovskite solar cells; ABX | |||||
| Saidi et al.[83] | 380 simulated ABX | Structural coordinates, lattice constants and octahedral angles | Predict bandgap | HCNN | RMSE 0.02 eV |
| Li et al.[101] | ABO | 66 descriptors generated from pymatgen package, and BVVS descriptor | Predict bandgap | SVM, RF, Bagging, GBT (best) | Test |
| Jin et al.[200] | 98 experimentally reported PV and 98 non-PV materials | 22 structural descriptors | Identify photovoltaic materials or not | GBT (best), SVM, RF, Adaboost, SGDC, CART, and LR | Accuracy 100% |
| Zhao et al.[84] | Synthesized 1400 perovskite samples | A-site ion, stoichiometry, coating methods, aging temperatures, humidity, and illumination | Predict | GBT (best), LR, and RF | CV RMSE 169 |
| Hartono et al.[81] | Synthesized 260 CL samples for MAPbI | 12 processing conditions and structural properties generated from PubChem database | Predict a key descriptor onset representing PSC stability | LR, KNN, RF (best), GBT, ANN, and SVM | CV RMSE 70.8 |
| Zhou et al.[203] | 9000 ab initio MD trajectories | Static and dynamic variables: 414 for 48-atom system, and 5440 for 384-atom system | Predict NAC and bandgap | KNN | |
| Lu et al.[224] | 539 HOIPs and 24 non-HOIPs from reported experiments | Elemental/organic properties and structural factors | Determine formability | CatBoost | LOOCV and test accuracies 100% |
| Zhang et al.[143] | 44 HOIs and 58 non-HOIPs from reported DFT calculations | Elemental/organic properties and structural factors | Determine formability (DFT) | XGBoost | LOOCV and test accuracies 91%-94% |
| Im et al.[225] | 540 simulated double halide perovskites | 32 features about atomic constituents and geometric information | Predict formation heat and bandgap | GBRT | Test RMSEs 0.021-0.223 eV |
| Li et al.[183] | 333 reported perovskite samples | Material compositions | Predict bandgap and PCE | LR, KNN, SVR, RF, ANN (best) | Test |
| Lu et al.[194] | 1109 perovskites/non-perovskites from reported first-principles calculations | Elemental and material properties | Predict formability, polar structure, bandgap | GBM | Accuracy 89% |
| Sun et al.[226] | Fabricated 75 perovskite films | XRD and absorption data | Classify 0D, 2D and 3D structures | ANN | Accuracy 90% |
| Wu et al.[179] | 1346 simulated HOIPs | 32 elemental properties and structural factors | Predict bandgap | GBR (best), SVR, KRR | |
| Yu et al.[157] | Synthesized 50 amines for post-treatment | Organic descriptors | Determine whether perovskite films are destroyed after post-treatment | LR, SVM (best), KNN, decision tree, Gaussian Naive Bayes | Test accuracy 86% |
| Lu et al.[227] | 346 HOIPs from reported first-principles calculations | 30 elemental and structural features | Predict bandgap | GBR (best), KRR, SVM, GPR, decision tree, ANN | Test |
| Li et al.[228] | 354 simulated halide perovskites | Elemental and structural features | Predict decomposition energy | KRR, KNN, SVR | RMSE 42-54 meV |
| Schmidt et al.[229] | 250000 simulated cubic perovskite materials | Elemental and structural features | Predict thermodynamic stability | RR, RF, extremely randomized tree, Adaboost (best), ANN | Test MAE 121.3 meV/atom |
As light absorbers, the bandgap is one of the most important properties for HOIPs and can act as a simple and initial criterion to rapidly inspect potential candidates. In this context, Saidi et al. established a complex hierarchical convolutional neural network (HCNN) to predict the bandgaps of ABX
Similar to the work of Saidi, Li et al. explored the chemical space of ABO
Figure 5. Overall workflow of progressive learning method. The schematic presents the details of a collection of perovskites and the outlines of a progressive learning workflow, including instrumental variable generation, bandgap (
Compared to the discovery of potential materials by predicting suitable bandgaps, Jin et al. established a classification model to directly identify 2D photovoltaic materials[200]. To perform the classification task, they collected 98 experimentally reported photovoltaic and 98 non-photovoltaic materials, accompanied by the generation of 22 structural descriptors that were evaluated and ranked by their feature importance. The packing factor (
Furthermore, Zhao et al. combined a robotic system, ML, and experiments [Figure 6] to assess the photothermal stability of APbI
Figure 6. (A) Crystal structure of a perovskite with multiple cations, including potassium (K
Considering that the addition of an inert capping layer (CL) might be beneficial to the stability of MAPbI
Motivated by the feature importance ranking, the authors further compared the top-performing CL material, namely, phenyltriethylammonium (PTEA), which had zero values for hydrogen-bond donors and TPSA, with other CLs via the methods of X-ray diffraction (XRD), scanning electron microscopy, grazing-incidence wide-angle-X-ray scattering and Fourier-transform infrared spectroscopy. The XRD data indicated that a new perovskite phase, (PTEA)
In addition to materials discovery, ML has also been applied to quantum dynamics to help uncover complex mechanisms, such as charge carrier trapping in perovskites. For example, Zhou et al. employed the KNN algorithm to analyze the calculated results from ab initio nonadiabatic MD and the most important structural factors for the charge carrier dynamics and bandgap of MAPbI
Data-driven progress in DSSCs
One of the advantages of DSSCs is the mature process of their device fabrication due to decades of their development and optimization in experimental conditions. Most ML/DL efforts so far have focused on accelerating the discovery of new organic dye sensitizers with notable photovoltaic properties that are promising for leading performance in DSSC devices. The typical ML publications of DSSCs are summarized in Table 6.
Typical ML publications of DSSCs
| Publication | Sample | Feature | ML Task | ML Algorithm | (Best) Model Performance |
| ML: Machine learning; DSSCs: Dye-sensitized solar cells; Dragon 7: a software to generate organic descriptors: https://chm.kode-solutions.net/; PaDEL: a software to generate organic descriptors: http://www.yapcwsoft.com/dd/padeldescriptor/; PLS: partial least squares; | |||||
| Krishna et al.[90] | 1200 reported dyes that could be divided into 7 chemical classes | Descriptors generated from Dragon 7 and PaDEL-descriptor software | Predict PCE | PLS | Test |
| Wen et al.[141] | 223 reported organic dyes | Descriptors extracted from DFT calculations | Predict PCE | GBT-SVM-ANN model with voting weight 4:7:4 | CV5 Test |
| Venkatraman et al.[207] | 1961 reported organic dyes | Descriptors generated from ISIDA Fragmentor2017 and RDKit | Predict the natures of spectral shift | LDA, KNN, SVM, CART, RF (best), and GBT | Accuracy 71%~81% |
| Lu et al.[93] | 58 reported BODIPY dyes | Descriptors generated from Dragon 7 | Predict PCE | MLR | cLOOCV Test |
| Cooper et al.[209] | 9431 dye materials generated from ChemDataExtractor | Chemical structures, absorption wavelengths, and molar extinction coefficients | Discover new co-sensitizers | Text-mining method | |
| Kar et al.[89] | 273 dye sensitizers | 248 constitutional descriptors generated from Dragon 6 | Predict PCE | MLR | Test |
| Venkatraman et al.[230] | 117 phenothiazine-based dye sensitizers | Molecular fragments | Predict PCE | PLS | Test |
Most recently, for the purpose of predicting the PCE values for DSSCs, Krishna et al. [Figure 7] prepared the largest (till 2020) dataset composed of over 1200 dyes that could be divided into seven chemical classes to form the corresponding datasets, including 207 phenothiazines, 229 triphenylamines, 35 diphenylamines, 179 carbazoles, 58 coumarins, 281 porphyrins, and 158 indolines, which cover both metal-based and metal-free dye sensitizers[90]. The dye structures in the seven datasets were depicted by Dragon software version 7[86] and PaDEL-descriptor software version 2.21[91] to generate the descriptors based on their 2D dye structures, containing constitutional information, ring counts, connectivity index, functional group counts, atom centered fragments, atom type E-states, 2D atom pairs, molecular properties and extended topochemical atom indices. Each dataset was split into a training set and a test set using either the Kennard-Stone[204] or modified k-medoid method[205] in a ratio of 7:3. The descriptor pool was pre-treated to eliminate the intercorrelated descriptors, followed by feature selection using the in-house program "Best Subset selection v2.1 software". Seven descriptor sets were extracted from the feature selection, where 13 descriptors were selected for triphenylamines, 14 for phenothiazines, 13 for indolines, 12 for porphyrins, 5 for coumarins, 11 for carbazoles, and 4 for diphenylamines. For each training set, five statistically acceptable and robust individual models (IMs) were developed.
Figure 7. Schematic representation of the steps involved in the development of QSPR models. Reproduced with permission from Krishna et al.[90] Copyright 2020 Elsevier.
To enhance the prediction quality of the test set, the authors further used their in-house intelligent consensus predictor tool[153] to perform "intelligent" selection based on these five multiple PLS models to complement the shortages of any single model in their test set predictions. Therefore, four types of consensus models (CMs) were developed, in which CM0 referred to as the ordinary consensus model, CM1 leveraged the average of the predictions from the qualified IMs, CM2 was the weighted average predictions from the qualified IMs, and CM3 signified the best model from the selected IMs. The CM3 model was the winning model for the triphenylamine, phenothiazine, indoline, and porphyrin datasets with determining coefficients
Afterwards, the authors discussed the mechanistic interpretations of all the descriptors obtained from the IMs for each dataset. For example, in total, ten descriptors appeared in the five IMs of the triphenylamine dataset, involving NdsN, B06[C-O], B07[O-S], B09[C-S], B06[O-S], C-038, C-043, nN(CO), EAT_Shape_Y, graph density, F05[N-N] and X4Av. NdsN represents the N atom numbers with double and single bonds (=N-), indicating the tendency of the localized
For the other six datasets, the authors completed a full analysis of the relationships among the descriptors, dye structures, and PCEs, as detailed in the original article. Inspired by the comprehensive discussions for the seven chemical classes, the authors designed ten coumarin dyes due to their low PCEs compared to all other studied chemical classes, in which the designed dyes showed a 20.68%-43.51% increase in PCE values (8.93%-10.62%) compared with the maximum reported experimental PCE value of 7.4%. Krishna and co-workers carried out a systematic investigation of the relationships between seven common kinds of organic dyes and device PCEs for DSSCs. More than 1200 dyes were collected and divided into seven datasets for building various PLS models. However, most of the PLS models exhibited relatively low
Wen et al. not only established an accurate, robust and interpretable ML model for predicting PCEs based on DFT-calculated descriptors, but also performed a virtual screening and the assessment of synthetic accessibility to identify new efficient and synthetically accessible organic dyes for DSSCs[141]. A database incorporating 223 reported organic dyes with experimental PCEs over 4% was built, along with the relaxed electronic structures optimized at the M06-2X/6-31G(d) level. The input features were comprised of 21 easily obtained descriptors extracted from the ground-state structures and statistical properties, such as orbital levels, atom counts, and dipole moments, which were further augmented by the expensively calculated vibrational, cationic, anionic, and excited-state properties. To achieve a compromise between the calculation costs and model accuracy, two models (models A and B) were built for the next 2 stepwise large-scale screenings, exerting only the simple and all features separately. Four algorithms, namely, RF, GBT, SVM, and ANN, were picked to perform the models. For model A, the
To enhance the prediction accuracy, the heterogeneous ensemble voting regressor model was built from the GBT, SVM, and ANN based on the voting weight of 4:7:4. The GBT-SVM-ANN model achieves partially higher accuracies with
In an earlier study, Venkatraman et al. explored the absorption shift of a dye sensitizer influenced by the adsorption on TiO
Our work concerning the data-driven discovery of novel DSSCs features the ML-aided design of new sensitizer materials based on BODIPY[93] and N-annulated perylene (N-P)[92]. Taking the case of BODIPY as an example, we collected a total of 58 BODIPY sensitizers that could be divided into horizontal and vertical types, with both types consisting of 29 samples. In contrast to the work of Krishna[90], we generated descriptors as much as possible to depict the structures of the sensitizers using Dragon and JChem software, resulting in 5515 dimensions of the features. A GA was employed to filter the descriptors for the two types of dataset, which were used to construct two LR models (horizontal and vertical models). The performance of the two models targeting PCEs achieved correlation coefficients
In the horizontal model, for example, the most important descriptor, Mor14p (see details in Section S2 and Figures S3 and S4), indicated that more conjugated structures and a larger number of C-S pairs contributed to the PCE values, stemming in the attachment of the groups, such as benzodithiophene, dithienothiophene, thiophene and similar. An additional C
The exploitation of new dye structures might have reached a bottleneck due to the scant absorption ability of singular organic molecules. The introduction of a co-sensitizer to expand the absorption capability is a practice alternative to enhance the performance of such devices. Cooper et al. probed the discovery of new co-sensitizer materials with panchromatic optical absorption for DSSCs using a design-to-device approach integrated with a high-throughput screening and text-mining method[209]. In total, 9431 dye materials were generated via the text-mining software ChemDataExtractor[210], including their chemical structures, maximum absorption wavelengths, and molar extinction coefficients. A stepwise screening based on statistics was then processed to shortlist the potential dye structures. In the initial stage, small molecules, organometallic dyes, and the materials that have no absorption in the solar spectra were first removed, leaving 3053 organic dyes. Two key structure-property data indicated the presence of a carboxylic acid group and a sufficiently large molecular dipole moment (over 5 D), which were applied to filter the remaining dyes, resulting in 309 dyes being shortlisted. This information suggested that the dyes contain a high-performance DSSC anchoring group, leading to the effective adsorption onto TiO
Afterwards, the authors developed a dye matching algorithm for further screening. Based on the known optical absorption peak wavelengths and extinction coefficients, each potential dye combination for co-sensitization could be ranked using a quality score. The algorithm ensured that the dye combination avoided the optical absorption overlap, exhibited panchromatic absorption, and had an improvement compared to any single dye, yielding 33 remaining dyes. Lately, the highest occupied molecular orbital (HOMO) and lowest-unoccupied molecular orbital (LUMO) energy levels were inspected by DFT. The dye candidate pool was reduced to 29 dyes after consideration of the criteria of LUMO energy level greater than -3.74 eV (TiO
Data-driven progress in OSCs
In spite of the long history of OSC studies, ML-related ones were scarce until 2018, which might be traced to the complex systems whose active layers mostly comprise binary or even ternary organic systems. Benefitting from the widespread of AI techniques and the stringent requirement for more efficient OSCs materials, ML and DL techniques are blooming to accelerate the process of discovering new potential PV materials for OSC devices. The main challenges issued from the AI work in the OSC field are mainly focused on 1) the representations of complex organic structures, particularly in blend systems, 2) the poor performance of the ML models with the currently maximum
Typical ML publications of OSCs
| Publication | Sample | Feature | ML Task | ML Algorithm | (Best) Model Performance |
| ML: Machine learning; OSCs: organic solar cells; NFA: non-fullerene acceptor; OPV: organic photovoltaic; PCE: power convection efficiency; ANN: artificial neural network; GBT: gradient boosting tree; SVM: support vector machine; KRR: kernel ridge regression; KNN: K-nearest neighbor; RF: random Forest; CV5: 5-fold Cross-validation; | |||||
| Kranthiraja et al[99] | 566 reported polymer-NFA OPV samples | Materials properties and fingerprints | Predict PCE | ANN, GBT, SVM, KRR, KNN, and RF (best) | CV5 |
| Wu et al.[148] | 565 reported donor-acceptor pairs | Fingerprints | Predict PCE | LR, LRC, RF (best), ANN, and GBT | CV10 MAE 0.832 |
| Zhao et al[212] | 566 reported organic donor-acceptor pairs | Fingerprints and quantum-based properties | Predict PCE | KNN (best), KRR, and SVM | LOOCV |
| Meftahi et al.[213] | 344 samples from Harvard Photovoltaic Dataset | Signature descriptors | Predict PCE, | BRANNLP | Training Test |
| Lee et al.[211] | 124 fullerene derivatives-based ternary OSCs samples | Theoretical orbital energies | Predict PCE | RF (best), GBT, KNN, LR, SVM | LOOCV Test |
| David et al.[218] | 1850 reported device data | 17 experimental conditions | Predict device stability | SMOreg | LOOCV Test |
| Du et al.[221] | 100 fabricated device data | 10-dimensional processing parameters | Predict photovoltaic performance | GP | Test RMSE 0.012 |
| Majeed et al.[231] | 20000 simulated device data | Light JV and dark JV curves | Predict electron and hole mobility, tail slope, and trap density | Deep neural network | |
| Pokuri et al.[232] | 65000 simulated morphologies | Images | Classify morphology | CNN | Accuracy 95.80% |
| Sahu et al.[233] | 300 reported small-molecule OPVs | 28 DFT descriptors | Predict PCE | GBRT (best), ANN, KNN | |
| Padula et al.[163] | 249 reported organic donor-acceptor pairs | DFT descriptors and fingerprints | Predict experimental photo voltaic parameters | KNN | |
| Sahu et al.[176] | 300 reported OPVs | Experimental device parameters and DFT descriptors | Predict PCE, | GBRT (best), RF | LOOCV |
| Sahu et al.[234] | 280 reported small-molecule OPVs | 13 DFT descriptors | Predict PCE | LR, KNN, ANN, RF, GBT (best) | LOOCV |
| Padula et al.[235] | 320 reported organic donor-acceptor pairs | DFT descriptors | Predict PCE | KRR (best), GPR, SVR, KNN | LOOCV |
| Nagasawa et al.[236] | 1200 reported cell devices | 1000 experimental parameters and fingerprints | Predict PCE | ANN, RF (best) | |
| Pyzer-Knapp et al.[182] | 266 reported donor materials | Fingerprints | Predict PCE, | GP | |
| Lopez et al.[68] | 51000 non-fullerene acceptors | 106 common moieties | Predict HOMO, LUMO | GP | |
Very recently and impressively, Kranthiraja et al. manually collected 566 polymer-NFA organic photovoltaic (OPV) samples from 253 publications before the end of 2018 to predict PCEs[99]. The descriptors were composed of the materials properties (MP) and FPs of the polymers (p) and NFA (n), in which MP included the HOMO, LUMO, bandgap, and molecular weight. The RF model was built up and examined by CV5 with the highest
To corroborate the model predicting result, the second-ranked polymer, labeled as PBDT(SBO)TzH, in the predicted PCE list of polymer-ITIC was selected for the synthesis, which consisted of benzodithiophene as the donor unit and thiazolothiazole (Tz) as that acceptor unit that were solubilized by sulfur-bridged 2-butyloctyl (BO) chains (SBO). However, the experimental PCE values in polymer-ITIC and -IT-4F were only 4.44% and 3.42% compared to the predicted values of 11.1% and 10.5%, which might be traceable from the poor solubility and rapid aggregation that was presumably not considered in the RF model. To ameliorate the flaws of PBDT(SBO)TzH, 4 variants were designed by replacing the SBO group that was responsible for the aggregation behavior and the varying the chains of the alkylthiophene-flanked Tz group that accounted for the poor solubility. One of the designed structures, marked as PBDTTzEH, showed a relatively similar experimental PCE value (10.10%) to the predicted one (11.17%), though the others still exhibited poor experimental PCE values of 2.15%, 3.97%, and 2.34% compared to the predicted values of 10.28%, 10.72%, and 10.70% due to the two unpromoted imperfections.
Experimental characteristics were measured to identify why PBDTTzEH had excellent performance. The
Another similar example could be seen in the work of Wu et al.[148] [Figure 8], which explored potential donor and acceptor materials for OSCs. They extracted 565 donor-acceptor pairs from 274 publications as the data samples to predict PCEs, in which each structure in both the donors and acceptors was divided into several fragments that were furtherly encoded by FPs. As a result, there were 31, 14, 27, and 14 in number for the 1-4 fragments for the donors and 30, 18, 6, 22, and 35 for the 1-5 fragments for the acceptors. Therefore, the description of each donor-acceptor sample was expressed by the FP's combinations of fragments. For the ML modeling, various algorithms of LR, LRC, RF, ANN, and GBT were performed based on the training data composed of
Figure 8. (A) Schematic of collecting experimental data and converting chemical structures to digitized data. (B) Schematic of machine training, prediction, and method evaluation. Reproduced with permission from Wu et al.[148], npj Comput. Mater. 6 (2020). Copyright 2020 Springer Nature.
By targeting the three high (
As discussed in the descriptor generation section, most input variables in the collected data are relevant to the processes of synthesis or testing, especially when the samples are sourced from experimental publications, which are far away from the molecular structures. To identify the relationship between material structures and their experimental properties, the descriptors depicting active layer structures are essentially needed, while the descriptor-based studies have been involved in the above cases. In such an instance, it is important to generate useful descriptors representing the structural information as the input variables for model building in the whole ML procedure. In the character of an organic structural scheme, particularly a binary or even ternary arrangement, describing such a complex organic absorber system in a numeric language remains a long-term crucial challenge, but also a promising and effective aspect of promoting the performance of ML models considering the large variety of descriptor choices that have been summarized in the descriptor generation section.
In the work of Zhao et al. [212], different kinds of descriptors were investigated for their effects in three ML models with the inclusion of KNN, KRR and SVM, in which the authors categorized them into structural (FPs) and physical (quantum-based) properties, including energy levels, molecule size, absorption, dipole moment, rotatable bonds and the partition coefficient between n-octanol and water, which was labeled as the XLOGP3 descriptor. The dataset included 566 organic donor-acceptor pairs composed of 513 donors and 33 acceptors. It is noteworthy that the authors refined the distance definition of the donor-acceptor pairs for the distance concept in the KNN and the kernel expressions in KRR and SVM, based on the linear distance combination weighted by the physical and structural descriptors of donors, acceptors, and whole systems.
Starting from five physical descriptors, including HOMO-D (where D is donor) to predict the PCE values, LUMO-D, LUMO-A (A is acceptor), reorganization energies of the polymer and acceptor, the LOOCV
Laying aside the traditionally and commonly used organic representations, Meftahi et al.[213] employed the so-called signature descriptors proposed by Pablo et al.[214] in 2013 into the ML work of predicting the quantum-based properties (such as energy levels) and the Scharber-model-based results[215] (such as PCE,
Despite the broad research in the OSC field, there is a significant lack of ML-related studies for the ternary system due to its complexity, in which only one publication[211], to the best of our knowledge, could be searched on the Web of Science. In Lee's work[211], a dataset of 124 fullerene derivatives-based ternary OSCs samples, regardless of the blend formations such as the composition of either one donor/two acceptors (D: A1:A2) or two donors/one acceptor (D1:D2:A) in the active layer, were constructed from the current literature, along with the theoretical orbital energies of donors, acceptors, and the whole systems. Targeting the PCE, the regression models of RF, GBT, KNN, LR, SVM, and the 99 training samples were undertaken, eventuating in the best performance with LOOCV
The analysis of the whole OSC device structure based on a large-scale dataset constituting both single and blend active layers had not been reported before the work of David et al.[218]. A dataset comprising 1850 device data was prepared, in which most were obtained from the Danish Technical University ranging from 2011 to 2017 and the remaining were manually scraped between 2017 and 2019. Regarding device stability, the numeric data of
Considering the 2 different testing conditions based on the International Summit on Organic Photovoltaic Stability (ISOS) protocols[219], the dataset involving 1149 samples after carefully data cleansing were treated in three modes: the full dataset with 1149 samples, the data (155) conducted with light soaking (ISOS-L) that relates to photostability, and the data (489) conducted with dark storage studies (ISOS-D) that provides information on the tolerance of the solar cells to oxygen, moisture, other aggressive atmospheric components naturally in air. The sequential minimal optimization regression (SMOreg) algorithm[220] was introduced into ML model building since it had the ability to produce the weights, namely the importance, of each feature, and thence help us to understand the feature significance, in which a positive SMOreg weighting corresponds to a positive influence on stability and the vice versa. The SMOreg model based on whole data signaled the LOOCV
Given the quantified significance from the weighting in SMOreg, several important features were identified. For instance, the features that most positively influenced the stability, namely,
Identical to the robotic work of Zhao et al. in the PSC field[84], Du et al. also utilized a high-throughput robot-based platform, "AMANDA Line One", to realize the superior precise control in experimental conditions at a very large scale so as to form high-quality and continuous sample points, which could also be expanded to the optimization in experimental details for any solution organic semiconductor and interface materials[221]. For this purpose, the authors fabricated around 100 OSC devices within photovoltaic performance (such as PCE,
CONCLUSION AND OUTLOOK
In this review, we have described the integral ML and DL training progress in section 2 and overviewed the recent ML and DL applications in the three fields of PSCs, DSSCs, and OSCs in section 3. Before training an ML/DL model, the first step is to collect samples along with their properties to form the dataset. The data sources in the most current publications are largely dependent on mature experimental and calculation databases, like the Materials Projects, ICSD, OQMD, and MPDS. With an increasing spread of high-throughput computations[83] and robotic experiments[84], more and more datasets with consistency and high quality will be produced and mined at the lab scale. To enhance the model performance, key attention should be devoted not only to the structural descriptors, such as the SMILE, molecular descriptors, fingerprints, and atomic descriptors, but also to the state-of-art modeling technologies, e.g., GCNN framework[120] and SISSO method[124]. Regarding model algorithms, the widely applied methods are sliced into the ensemble algorithms, especially GBM derivatives and the DL models, such as deep ANN and CNN. As the algorithms develop, we may see more occurrences of more predictive and advanced model algorithms in the future, such as GAN, VAE, RNN, and LSTM networks. Given an established model, the most practiced method to apply the model is to perform high-throughput screening to filter the potential candidates, in which the search space should be restrained and the candidates need to be shortlisted by domain knowledge. Another method is to understand the established models by combining domain knowledge and feature interpretation via various analysis tools, such as the SHAP method[39, 143].
In summary, with the fast-developing ML and DL technologies, data-driven methods combined with domain knowledge will exhibit more robust performance and accurate prediction power in materials science beyond photovoltaic fields, with the potential to be an indispensable analysis tool for both experiments and quantum-based computations in the future.
DECLARATIONS
Availability of data and materials
Supporting information available: details of outlier detection algorithms; Illustration for descriptors Mor14p, Mor24m, R2s; Atomic parameters.
Authors' contributions
Wrote the manuscript: Lu T
Supervised this manuscript: Li M, Lu W, Zhang TY
Conflicts of interest
The authors declared that there are no competing financial interest.
Financial support and sponsorship
This study was supported by the National Key Research and Development Program of China (No.2018YFB0704400), the Key Research Project of Zhejiang Laboratory (No.2021PE0AC02), and Shanghai Pujiang Program (21PJD024).
Ethical approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Copyright
© The Author(s) 2022.
Supplementary Materials
REFERENCES
1. Hadadian M, Smått J, Correa-baena J. The role of carbon-based materials in enhancing the stability of perovskite solar cells. Energy Environ Sci 2020;13:1377-407.
2. Liu Y, Li Y, Wu Y, et al. High-efficiency silicon heterojunction solar cells: materials, devices and applications. Mater Sci Eng: R: Rep 2020;142:100579.
3. Kim M, Ham S, Cheng D, Wynn TA, Jung HS, Meng YS. Advanced characterization techniques for overcoming challenges of perovskite solar cell materials. Adv Energy Mater 2021;11:2001753.
4. Li H, Li F, Shen Z, et al. Photoferroelectric perovskite solar cells: principles, advances and insights. Nano Today 2021;37:101062.
5. L. R. Devereux, J. M. Cole. in Data science applied to sustainability analysis, edited by Jennifer Dunn and Prasanna Balaprakash (Elsevier, 2021), pp. 129.
6. Kojima A, Teshima K, Shirai Y, Miyasaka T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J Am Chem Soc 2009;131:6050-1.
7. Zhang F, Lu H, Tong J, Berry JJ, Beard MC, Zhu K. Advances in two-dimensional organic-inorganic hybrid perovskites. Energy Environ Sci 2020;13:1154-86.
8. Kim G, Min H, Lee KS, Lee DY, Yoon SM, Seok SI. Impact of strain relaxation on performance of α-formamidinium lead iodide perovskite solar cells. Science 2020;370:108-12.
9. Green MA, Dunlop ED, Hohl-ebinger J, Yoshita M, Kopidakis N, Hao X. Solar cell efficiency tables (Version 58). Prog Photovolt Res Appl 2021;29:657-67.
10. NREL, Best research-cell efficiency chart. Available from: https://www.nrel.gov/pv/cell-efficiency.html [Last accessed on 8 Jun 2022].
11. Luo Q, Wu R, Ma L, et al. Recent advances in carbon nanotube utilizations in perovskite solar cells. Adv Funct Mater 2021;31:2004765.
12. Luo D, Su R, Zhang W, Gong Q, Zhu R. Minimizing non-radiative recombination losses in perovskite solar cells. Nat Rev Mater 2020;5:44-60.
14. O'regan B, Grätzel M. A low-cost, high-efficiency solar cell based on dye-sensitized colloidal TiO2 films. Nature 1991;353:737-40.
15. Zeng K, Tong Z, Ma L, Zhu W, Wu W, Xie Y. Molecular engineering strategies for fabricating efficient porphyrin-based dye-sensitized solar cells. Energy Environ Sci 2020;13:1617-57.
16. Kakiage K, Aoyama Y, Yano T, Oya K, Fujisawa J, Hanaya M. Highly-efficient dye-sensitized solar cells with collaborative sensitization by silyl-anchor and carboxy-anchor dyes. Chem Commun (Camb) 2015;51:15894-7.
18. Armin A, Li W, Sandberg OJ, et al. A history and perspective of non-fullerene electron acceptors for organic solar cells. Adv Energy Mater 2021;11:2003570.
19. Luo Z, Liu T, Yan H, Zou Y, Yang C. Isomerization strategy of nonfullerene small-molecule acceptors for organic solar cells. Adv Funct Mater 2020;30:2004477.
20. Zheng Z, Yao H, Ye L, Xu Y, Zhang S, Hou J. PBDB-T and its derivatives: a family of polymer donors enables over 17% efficiency in organic photovoltaics. Mater Today 2020;35:115-30.
21. Mishra A. Material perceptions and advances in molecular heteroacenes for organic solar cells. Energy Environ Sci 2020;13:4738-93.
22. Kini GP, Jeon SJ, Moon DK. Latest progress on photoabsorbent materials for multifunctional semitransparent organic solar cells. Adv Funct Mater 2021;31:2007931.
23. Zhao C, Wang J, Zhao X, Du Z, Yang R, Tang J. Recent advances, challenges and prospects in ternary organic solar cells. Nanoscale 2021;13:2181-208.
24. Schmidt J, Marques MRG, Botti S, Marques MAL. Recent advances and applications of machine learning in solid-state materials science. npj Comput Mater 2019:5.
26. Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys Rev 1965;140:A1133-8.
28. Luo S, Zeng Z, Wang H, et al. Recent progress in conjugated microporous polymers for clean energy: synthesis, modification, computer simulations, and applications. Progress in Polymer Science 2021;115:101374.
29. Chen C, Zuo Y, Ye W, Li X, Deng Z, Ong SP. A critical review of machine learning of energy materials. Adv Energy Mater 2020;10:1903242.
30. Haghighatlari M, Vishwakarma G, Altarawy D, et al. ChemML: a machine learning and informatics program package for the analysis, mining, and modeling of chemical and materials data. WIREs Comput Mol Sci 2020:10.
31. Moosavi SM, Jablonka KM, Smit B. The role of machine learning in the understanding and design of materials. J Am Chem Soc 2020:20273-87.
32. Chen L, Pilania G, Batra R, et al. Polymer informatics: current status and critical next steps. Mater Sci Eng: R: Rep 2021;144:100595.
33. Masood H, Toe CY, Teoh WY, Sethu V, Amal R. Machine learning for accelerated discovery of solar photocatalysts. ACS Catal 2019;9:11774-87.
34. Jia Y, Hou X, Wang Z, Hu X. Machine learning boosts the design and discovery of nanomaterials. ACS Sustainable Chem Eng 2021;9:6130-47.
35. Brown KA, Brittman S, Maccaferri N, Jariwala D, Celano U. Machine learning in nanoscience: big data at small scales. Nano Lett 2020;20:2-10.
37. Halevy A, Norvig P, Pereira F. The unreasonable effectiveness of data. IEEE Intell Syst 2009;24:8-12.
38. Jablonka KM, Ongari D, Moosavi SM, Smit B. Big-data science in porous materials: materials genomics and machine learning. Chem Rev 2020;120:8066-129.
39. Xiong J, Shi S, Zhang T. Machine learning of phases and mechanical properties in complex concentrated alloys. J Mater Sci Technol 2021;87:133-42.
40. BONEAU CA. The effects of violations of assumptions underlying the test. Psychol Bull 1960;57:49-64.
41. Edgell SE, Noon SM. Effect of violation of normality on the t test of the correlation coefficient. Psychological Bulletin 1984;95:576-83.
42. R. G. Lomax, An introduction to statistical concepts. (Mahwah, N.J. : Lawrence Erlbaum Associates Publishers, 2007), p. 10.
43. Breunig MM, Kriegel H, Ng RT, Sander J. LOF: identifying density-based local outliers. SIGMOD Rec 2000;29:93-104.
44. Liu FT, Ting KM, Zhou Z. Isolation-based anomaly detection. ACM Trans Knowl Discov Data 2012;6:1-39.
46. Rousseeuw PJ, Driessen KV. A fast algorithm for the minimum covariance determinant estimator. Technometrics 1999;41:212-23.
47. Schölkopf B, Platt JC, Shawe-Taylor J, Smola AJ, Williamson RC. Estimating the support of a high-dimensional distribution. Neural Comput 2001;13:1443-71.
48. Chang C, Lin C. LIBSVM: A library for support vector machines. ACM Trans Intell Syst Technol 2011;2:1-27.
49. Zhao Y, Hryniewicki MK. Improving supervised outlier detection with unsupervised representation learning. Available from: https://arxiv.org/abs/1912.00290 [Last accessed on 10 Jun 2022].
50. Chen T, Guestrin C. XGBoost: a scalable tree boosting system (2016), https://xgboost.readthedocs.io/en/latest/install.html.
51. Dorogush AV, Ershove V, Guilin A. CatBoost: gradient boosting with categorical features support (2018). Available from: https://catboost.ai/docs [Last accessed on 8 Jun 2022].
52. Jain A, Ong SP, Hautier G, et al. Commentary: the materials project: a materials genome approach to accelerating materials innovation. APL Materials 2013;1:011002.
53. Zagorac D, Müller H, Ruehl S, Zagorac J, Rehme S. Recent developments in the inorganic crystal structure database: theoretical crystal structure data and related features. J Appl Crystallogr 2019;52:918-25.
54. Saal JE, Kirklin S, Aykol M, Meredig B, Wolverton C. Materials design and discovery with high-throughput density functional theory: The open quantum materials database (OQMD). JOM 2013;65:1501-9.
55. Kirklin S, Saal JE, Meredig B, et al. The open quantum materials database (OQMD): assessing the accuracy of DFT formation energies. npj Comput Mater 2015:1.
56. P. Villars. Materials platform for data science (2019). Available from: https://mpds.io/ [Last accessed on 8 Jun 2022].
57. Su Y. Materials genome engineering databases (University of Science and Technology Beijing, 2018). Available from: https://www.mgedata.cn/ [Last accessed on 8 Jun 2022].
58. Qian Q, Wang Y, Zhao S. Materials data specification: methods and use cases. Comput Mater Sci 2019;169:109086.
59. Tao Q, Xu P, Li M, Lu W. Machine learning for perovskite materials design and discovery. npj Comput Mater 2021:7.
61. Groom CR, Bruno IJ, Lightfoot MP, Ward SC. The cambridge structural database. Acta Cryst 2016;72:171-9.
62. Grazulis S, Chateigner D, Downs RT, Yokochi AFT, Quiros M, Lutterotti L, Manakova E, Butkus J, Moeck P, Bail AL. Crystallography open database - an open-access collection of crystal structures. J Appl Crystallogr 2009;42:726-9.
63. Gómez-Bombarelli R, Wei JN, Duvenaud D, et al. Automatic chemical design using a data-driven continuous representation of molecules. ACS Cent Sci 2018;4:268-76.
64. G. Landrum. RDKit: Open-source cheminformatics (2012). Available from: http://www.rdkit.org/ [Last accessed on 8 Jun 2022].
65. Ramakrishnan R, Dral PO, Rupp M, von Lilienfeld OA. Quantum chemistry structures and properties of 134 kilo molecules. Sci Data 2014;1:140022.
66. Irwin JJ, Sterling T, Mysinger MM, Bolstad ES, Coleman RG. ZINC: a free tool to discover chemistry for biology. J Chem Inf Model 2012;52:1757-68.
67. IBM. World Community Grid. Available from: http://www.worldcommunitygrid.org/ [Last accessed on 8 Jun 2022].
68. Lopez SA, Sanchez-lengeling B, de Goes Soares J, Aspuru-guzik A. Design principles and top non-fullerene acceptor candidates for organic photovoltaics. Joule 2017;1:857-70.
69. Lopez SA, Pyzer-Knapp EO, Simm GN, et al. The Harvard organic photovoltaic dataset. Sci Data 2016;3:160086.
70. Venkatraman V, Raju R, Oikonomopoulos SP, Alsberg BK. The dye-sensitized solar cell database. J Cheminform 2018;10:18.
71. Odabaşı Ç, Yıldırım R. Performance analysis of perovskite solar cells in 2013-2018 using machine-learning tools. Nano Energy 2019;56:770-91.
72. Odabaşı Ç, Yıldırım R. Machine learning analysis on stability of perovskite solar cells. Sol Energy Mater Sol Cells 2020;205:110284.
73. Odabaşı Ç, Yıldırım R. Assessment of reproducibility, hysteresis, and stability relations in perovskite solar cells using machine learning. Energy Technol 2020;8:1901449.
74. Yılmaz B, Yıldırım R. Critical review of machine learning applications in perovskite solar research. Nano Energy 2021;80:105546.
75. D. Systèmes, BIOVIA MATERIALS STUDIO (Dassault Systèmes, 2002-2021). Available from: https://www.3ds.com/products-services/biovia/products/molecular-modeling-simulation/biovia-materials-studio/ [Last access on 8 Jun 2022].
76. Kresse G, Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput Mater Sci 1996;6:15-50.
77. Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B Condens Matter 1996;54:11169-86.
78. Kresse G, Hafner J. Ab initio molecular dynamics for liquid metals. Phys Rev B Condens Matter 1993;47:558-61.
79. Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys Rev B 1999;59:1758-75.
80. Frisch MJ, Trucks GW, Schlegel HB et al. Gaussian 16 Rev. C. 01. Available from: https://gaussian.com/citation_b01/ [Last accessed on 10Jun 2022].
81. Hartono NTP, Thapa J, Tiihonen A, et al. How machine learning can help select capping layers to suppress perovskite degradation. Nat Commun 2020;11:4172.
82. Lundberg SM, Erion G, Chen H, et al. From local explanations to global understanding with explainable AI for trees. Nat Mach Intell 2020;2:56-67.
83. Saidi WA, Shadid W, Castelli IE. Machine-learning structural and electronic properties of metal halide perovskites using a hierarchical convolutional neural network. npj Comput Mater 2020:6.
84. Zhao Y, Zhang J, Xu Z, et al. Discovery of temperature-induced stability reversal in perovskites using high-throughput robotic learning. Nat Commun 2021;12:2191.
85. Mahmood A, Wang J. Machine learning for high performance organic solar cells: current scenario and future prospects. Energy Environ Sci 2021;14:90-105.
86. Kode-Chemoinformatics. Dragon 7 (2021). Available from: https://gaussian.com/citation_b01/ [Last accessed on 8 Jun 2022].
87. Available from: https://match.pmf.kg.ac.rs/electronic_versions/Match56/n2/match56n2_237-248.pdf [Last accessed on 10 Jun 2022].
88. Krenn M, Häse F, Nigam A, Friederich P, Aspuru-guzik A. Self-referencing embedded strings (SELFIES): a 100% robust molecular string representation. Mach Learn : Sci Technol 2020;1:045024.
89. Kar S, Roy JK, Leszczynski J. In silico designing of power conversion efficient organic lead dyes for solar cells using todays innovative approaches to assure renewable energy for future. npj Comput Mater 2017:3.
90. Krishna JG, Ojha PK, Kar S, Roy K, Leszczynski J. Chemometric modeling of power conversion efficiency of organic dyes in dye sensitized solar cells for the future renewable energy. Nano Energy 2020;70:104537.
91. Yap CW. PaDEL-descriptor: an open source software to calculate molecular descriptors and fingerprints. J Comput Chem 2011;32:1466-74.
92. Ju L, Li M, Tian L, Xu P, Lu W. Accelerated discovery of high-efficient N-annulated perylene organic sensitizers for solar cells via machine learning and quantum chemistry. Mater Today Commun 2020;25:101604.
93. Lu T, Li M, Yao Z, Lu W. Accelerated discovery of boron-dipyrromethene sensitizer for solar cells by integrating data mining and first principle. J Mater 2021;7:790-801.
94. Shemetulskis NE, Weininger D, Blankley CJ, Yang JJ, Humblet C. Stigmata: an algorithm to determine structural commonalities in diverse datasets. J Chem Inf Comput Sci 1996;36:862-71.
95. Cereto-Massagué A, Ojeda MJ, Valls C, Mulero M, Garcia-Vallvé S, Pujadas G. Molecular fingerprint similarity search in virtual screening. Methods 2015;71:58-63.
96. Muegge I, Mukherjee P. An overview of molecular fingerprint similarity search in virtual screening. Expert Opin Drug Discov 2016;11:137-48.
97. Pattanaik L, Coley CW. Molecular representation: going long on fingerprints. Chem 2020;6:1204-7.
98. Sun W, Zheng Y, Yang K, et al. Machine learning-assisted molecular design and efficiency prediction for high-performance organic photovoltaic materials. Sci Adv 2019;5:eaay4275.
99. Kranthiraja K, Saeki A. Experiment-oriented machine learning of polymer: non-fullerene organic solar cells. Adv Funct Mater 2021;31:2011168.
100. Lo. Mentel. mendeleev - a python resource for properties of chemical elements, ions and isotopes (2014). Available from: https://github.com/lmmentel/mendeleev [Last accessed on 8 Jun 2022].
101. Li C, Hao H, Xu B, et al. A progressive learning method for predicting the band gap of ABO$$_3$$ perovskites using an instrumental variable. J Mater Chem C 2020;8:3127-36.
102. Ong SP, Richards WD, Jain A, et al. Python materials genomics (pymatgen): a robust, open-source python library for materials analysis. Comput Mater Sci 2013;68:314-9.
103. Pilania G, Balachandran PV, Kim C, Lookman T. Finding new perovskite halides via machine learning. Front Mater 2016:3.
104. N. Chen, Bond parameter function and application (In Chinese), 1st ed. (CHINA SCIENCE PUBLISHING & MEDIA LTD, Beijing, China, 1976.
106. Available from: https://jsc.niic.nsc.ru/ [Last accessed on 10 Jun 2022].
107. Pauling L. The nature of the chemical bond. application of results obtained from the quantum mechanics and from a theory of paramagnetic susceptibility to the structure of molecules. J Am Chem Soc 1931;53:1367-400.
109. Zachariasen WH. A set of empirical crystal radii for ions with inert gas configuration. Zeitschrift für Kristallographie - Crystalline Materials 1931;80:137-53.
111. Beskow G. V. M. Goldschmidt: geochemische verteilungsgesetze der elemente. Geologiska Föreningen i Stockholm Förhandlingar 2010;46:738-43.
112. Lu W, Lv W, Zhang Q, Lu K, Ji X. Material data mining in Nianyi Chen's scientific family: material data mining in Nianyi Chen's scientific family. J Chemom 2018;32:e3022.
113. Murray JS, Lane P, Brinck T, Paulsen K, Grice ME, Politzer P. Relationships of critical constants and boiling points to computed molecular surface properties. J Phys Chem 1993;97:9369-73.
114. Byrd EF, Rice BM. Improved prediction of heats of formation of energetic materials using quantum mechanical calculations. J Phys Chem A 2006;110:1005-13.
115. Rice BM, Byrd EF. Evaluation of electrostatic descriptors for predicting crystalline density. J Comput Chem 2013;34:2146-51.
116. T. Lu. fast machine learning (2021). Available from: https://pypi.org/project/fast-machine-learning/ [Last accessed on 8 Jun 2022].
117. Sun W, Li M, Li Y, et al. The use of deep learning to fast evaluate organic photovoltaic materials. Adv Theory Simul 2019;2:1800116.
118. Jang J, Gu GH, Noh J, Kim J, Jung Y. Structure-based synthesizability prediction of crystals using partially supervised learning. J Am Chem Soc 2020;142:18836-43.
119. Chen C, Ye W, Zuo Y, Zheng C, Ong SP. Graph networks as a universal machine learning framework for molecules and crystals. Chem Mater 2019;31:3564-72.
120. Xie T, Grossman JC. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys Rev Lett 2018;120:145301.
121. T. Stephens. gplearn: Genetic Programming in Python (2016). Available from: https://gplearn.readthedocs.io/ [Last accessed on 8 Jun 2022].
122. Fortin FA, Rainville FMD, Gardner MA, Parizeau M, Gagné C. DEAP: Evolutionary Algorithms Made Easy J Mach Learn Res 13, 2171 (2012). Available from: https://www.jmlr.org/papers/v13/fortin12a.html[last accessed on 10 Jun 2022].
123. Ouyang R, Curtarolo S, Ahmetcik E, Scheffler M, Ghiringhelli LM. SISSO: a compressed-sensing method for identifying the best low-dimensional descriptor in an immensity of offered candidates. Phys Rev Materials 2018:2.
124. Bartel CJ, Sutton C, Goldsmith BR, et al. New tolerance factor to predict the stability of perovskite oxides and halides. Sci Adv 2019;5:eaav0693.
125. Varoquaux G, Gramfort A, Pedregosa F, Michel V, Thirion B. Multi-subject dictionary learning to segment an atlas of brain spontaneous activity. J Mach Learn Res 2011;12:2825.
126. Golbraikh A, Shen M, Xiao Z, Xiao Y, Lee K, Tropsha A. Rational selection of training and test sets for the development of validated QSAR models. J Comput Aided Mol Des 2003;17:241-53.
127. Golbraikh A, Tropsha A. Predictive QSAR modeling based on diversity sampling of experimental datasets for the training and test set selection. Mol Divers 2000;5:231-43.
128. Chandrashekar G, Sahin F. A survey on feature selection methods. Comput Electr Eng 2014;40:16-28.
129. Guyon I, Nikravesh M, Gunn S, Zadeh LA. Feature Extraction. Fuzziness Soft Comput 2006;207:778.
130. Ding C, Peng H. Minimum redundancy feature selection from microarray gene expression data. J Bioinform Comput Biol 2005;3:185-205.
131. Peng H, Long F, Ding C. Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans Pattern Anal Mach Intell 2005;27:1226-38.
132. Ramírez-gallego S, Lastra I, Martínez-rego D, et al. Fast-mRMR: fast minimum redundancy maximum relevance algorithm for high-dimensional big data: fast-mRMR algorithm for big data. Int J Intell Syst 2017;32:134-52.
133. Guyon I, Weston J, Barnhill S, Vapnik V. Gene selection for cancer classification using support vector machines. Machine Learning 2022;46:389-422.
134. Genetic programming in python, with a scikit-learn inspired API (2016), https://gplearn.readthedocs.io/ [Last accessed on 8 Jun 2022].
135. Collette Y, Hansen N, Pujol G, Salazar Aponte D, Le Riche R. In multidisciplinary design optimization in computational mechanics (2013), pp. 499.
136. S. Mirjalili. in Evolutionary algorithms and neural networks: theory and applications, edited by Seyedali Mirjalili. Springer International Publishing: Cham; 2019. pp. 43.
138. Ferri F, Pudil P, Hatef M, Kittler J. Comparative study of techniques for large-scale feature selection. Comparative Studies and Hybrid Systems. Elsevier; 1994. pp. 403-13.
140. L. Breiman, J. H. Friedman, and R. A. Olshen, Classification and regression trees. (Wadsworth International Group, Belmont, CA, 1984).
141. Wen Y, Fu L, Li G, Ma J, Ma H. Accelerated discovery of potential organic dyes for dye-sensitized solar cells by interpretable machine learning models and virtual screening. Sol RRL 2020;4:2000110.
143. Zhang S, Lu T, Xu P, Tao Q, Li M, Lu W. Predicting the formability of hybrid organic-inorganic perovskites via an interpretable machine learning strategy. J Phys Chem Lett 2021;12:7423-30.
144. Guolin K, Qi M, Thomas F, Taifeng W, et al. In advances in neural information processing systems 30 (NIPS 2017) (Long Beach, CA, USA, 2017).
145. Paszke A, Gross S, Massa F, et al. PyTorch: an imperative style, high-performance deep learning library. (Curran Associates, Inc, 2019), pp. 8024. Available from: https://proceedings.neurips.cc/paper/2019/file/bdbca288fee7f92f2bfa9f7012727740-Paper.pdf [Last accessed on 13 Jun 2022].
146. M. Abadi, A. Agarwal, P. Barham, et al. TensorFlow: large-scale machine learning on heterogeneous systems (2015). Available from: https://arxiv.org/abs/1603.04467 [Last accessed on 13 Jun 2022].
147. Zárate Hernández LA, Camacho-Mendoza RL, González-Montiel S, Cruz-Borbolla J. The chemical reactivity and QSPR of organic compounds applied to dye-sensitized solar cells using DFT. J Mol Graph Model 2021;104:107852.
148. Wu Y, Guo J, Sun R, Min J. Machine learning for accelerating the discovery of high-performance donor/acceptor pairs in non-fullerene organic solar cells. npj Comput Mater 2020:6.
149. David TW, Anizelli H, Tyagi P, Gray C, Teahan W, Kettle J. Using large datasets of organic photovoltaic performance data to elucidate trends in reliability between 2009 and 2019. IEEE J Photovoltaics 2019;9:1768-73.
150. Kar S, Roy J, Leszczynska D, Leszczynski J. Power conversion efficiency of arylamine organic dyes for dye-sensitized solar cells (DSSCs) explicit to cobalt electrolyte: understanding the structural attributes using a direct QSPR approach. Computation 2017;5:2.
151. Roy JK, Kar S, Leszczynski J. Insight into the optoelectronic properties of designed solar cells efficient tetrahydroquinoline dye-sensitizers on TiO2(101) surface: first principles approach. Sci Rep 2018;8:10997.
152. Roy JK, Kar S, Leszczynski J. Electronic structure and optical properties of designed photo-efficient indoline-based dye-sensitizers with D-A-$$\pi$$-A framework. J Phys Chem C 2019;123:3309-20.
153. Roy K, Ambure P, Kar S, Ojha PK. Is it possible to improve the quality of predictions from an "intelligent" use of multiple QSAR/QSPR/QSTR models?: quality of predictions from an "intelligent" use of multiple models. J Chemom 2018;32:e2992.
155. Tolles J, Meurer WJ. Logistic regression: relating patient characteristics to outcomes. JAMA 2016;316:533-4.
156. Walker SH, Duncan DB. Estimation of the probability of an event as a function of several independent variables. Biometrika 1967;54:167.
157. Yu Y, Tan X, Ning S, Wu Y. Machine learning for understanding compatibility of organic-inorganic hybrid perovskites with post-treatment amines. ACS Energy Lett 2019;4:397-404.
158. Friedman J., Hastie T., Tibshirani R. Regularization paths for generalized linear models via coordinate descent. J Stat Softw 2010:33.
159. Santosa F, Symes WW. Linear inversion of band-limited reflection seismograms. SIAM J Sci and Stat Comput 1986;7:1307-30.
160. Hoerl AE, Kennard RW. Ridge regression: biased estimation for nonorthogonal problems. Technometrics 1970;12:55-67.
161. Li X, Dan Y, Dong R, et al. Computational screening of new perovskite materials using transfer learning and deep learning. Appl Sci 2019;9:5510.
162. Stoddard RJ, Dunlap-shohl WA, Qiao H, Meng Y, Kau WF, Hillhouse HW. Forecasting the decay of hybrid perovskite performance using optical transmittance or reflected dark-field imaging. ACS Energy Lett 2020;5:946-54.
163. Padula D, Simpson JD, Troisi A. Combining electronic and structural features in machine learning models to predict organic solar cells properties. Mater Horiz 2019;6:343-9.
164. Wu X, Kumar V, Ross Quinlan J, et al. Top 10 algorithms in data mining. Knowl Inf Syst 2008;14:1-37.
165. Raccuglia P, Elbert KC, Adler PD, et al. Machine-learning-assisted materials discovery using failed experiments. Nature 2016;533:73-6.
166. Jiménez-luna J, Grisoni F, Schneider G. Drug discovery with explainable artificial intelligence. Nat Mach Intell 2020;2:573-84.
167. Breiman L. Pasting small votes for classification in large databases and on-line. Machine Learning 1999;36:85-103.
169. Tin Kam Ho. The random subspace method for constructing decision forests. IEEE Trans Pattern Anal Machine Intell ;20:832-44.
170. Louppe G, Geurts P. Ensembles on random patches. (Springer Berlin Heidelberg, Berlin, Heidelberg, 2012), pp. 346. Available from: https://link.springer.com/chapter/10.1007/978-3-642-33460-3_28 [Last accessed on 13 Jun 2022].
171. Takahashi K, Takahashi L, Miyazato I, Tanaka Y. Searching for hidden perovskite materials for photovoltaic systems by combining data science and first principle calculations. ACS Photonics 2018;5:771-5.
172. Freund Y, Schapire RE. A decision-theoretic generalization of on-line learning and an application to boosting. J Comput and Sys Sci 1997;55:119-39.
173. J. H. Friedman, Greedy function approximation: a gradient boosting machine. Ann. Stat 2001; 29, 1189 (2001),.
174. G. Ke, Q. Meng, T. Finley, T. Wang, W. Chen, W. Ma, Q. Ye, and T. -Y. Liu, in Proceedings of the 31st International Conference on Neural Information Processing Systems (Curran Associates Inc., Long Beach, California, USA, 2017), pp. 3149.
175. Prokhorenkova L, . Gusev G, A. Vorobev, A. V. Dorogush, A. Gulin. CatBoost: unbiased boosting with categorical features. Available from: https://arxiv.org/abs/1706.09516 [Last accessed on 13 Jun 2022].
176. Sahu H, Ma H. Unraveling correlations between molecular properties and device parameters of organic solar cells using machine learning. J Phys Chem Lett 2019;10:7277-84.
179. Wu T, Wang J. Global discovery of stable and non-toxic hybrid organic-inorganic perovskites for photovoltaic systems by combining machine learning method with first principle calculations. Nano Energy 2019;66:104070.
180. Ambikasaran S, Foreman-Mackey D, Greengard L, Hogg DW, O'Neil M. Fast direct methods for gaussian processes. IEEE Trans Pattern Anal Mach Intell 2016;38:252-65.
182. Pyzer-knapp EO, Simm GN, Aspuru Guzik A. A Bayesian approach to calibrating high-throughput virtual screening results and application to organic photovoltaic materials. Mater Horiz 2016;3:226-33.
183. Li J, Pradhan B, Gaur S, Thomas J. Predictions and strategies learned from machine learning to develop high-performing perovskite solar cells. Adv Energy Mater 2019;9:1901891.
184. Sanchez-Lengeling B, Aspuru-Guzik A. Inverse molecular design using machine learning: generative models for matter engineering. Science 2018;361:360-5.
185. Creswell A, White T, Dumoulin V, Arulkumaran K, Sengupta B, Bharath AA. Generative adversarial networks: an overview. IEEE Signal Process Mag 2018;35:53-65.
186. Goodfellow I, Pouget-abadie J, Mirza M, et al. Generative adversarial networks. Commun ACM 2020;63: 139-44. Available from: https://proceedings.neurips.cc/paper/2014/hash/5ca3e9b122f61f8f06494c97b1afccf3-Abstract.html [Last accessed on 13 Jun 2022].
187. Goodfellow I J, Pouget-Abadie J, Mirza M, et al. Generative Adversarial Networks. 2014. Available from: https://arxiv.org/abs/1406.2661 [Last accessed on 13 Jun 2022].
188. Kingma D P, Welling M. Auto-encoding variational bayes. Available from: https://arxiv.org/abs/1312.6114 [Last accessed on 13 Jun 2022].
189. Rousseeuw PJ. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J Comput Appl Math 1987;20:53-65.
190. Choudhary K, Bercx M, Jiang J, Pachter R, Lamoen D, Tavazza F. Accelerated discovery of efficient solar-cell materials using quantum and machine-learning methods. Chem Mater 2019;31:5900-8.
191. Komer B, Socastro MT, Kim W. Hyperopt: distributed hyperparameter optimization (2012-2021). Available from: https://github.com/hyperopt/hyperopt [Last accessed on 9 Jun 2022].
192. Akiba T, Sano S, Yanase T, Ohta T, Koyama M. A next-generation hyperparameter optimization framework. Preferred Networks, Inc., 2017-2021.
193. Liaw R, Liang E, Nishihara R, Moritz P, Gonzalez JE, Stoica I. tune: scalable hyperparameter tuning (The Ray Team, 2018). Available from: https://docs.ray.io/en/latest/tune/index.html [Last accessed on 10 Jun 2022].
194. Lu S, Zhou Q, Ma L, Guo Y, Wang J. Rapid discovery of ferroelectric photovoltaic perovskites and material descriptors via machine learning. Small Methods 2019;3:1900360.
195. Kim C, Pilania G, Ramprasad R. Machine learning assisted predictions of intrinsic dielectric breakdown strength of ABX3 perovskites. J Phys Chem C 2016;120:14575-80.
196. Körbel S, Marques MAL, Botti S. Stability and electronic properties of new inorganic perovskites from high-throughput ab initio calculations. J Mater Chem C 2016;4:3157-67.
197. Gómez-Bombarelli R, Aguilera-Iparraguirre J, Hirzel TD, et al. Design of efficient molecular organic light-emitting diodes by a high-throughput virtual screening and experimental approach. Nat Mater 2016;15:1120-7.
198. Tao Q, Lu T, Sheng Y, Li L, Lu W, Li M. Machine learning aided design of perovskite oxide materials for photocatalytic water splitting. J Energy Chem 2021;60:351-9.
199. Xu P, Lu T, Ju L, Tian L, Li M, Lu W. Machine learning aided design of polymer with targeted band gap based on DFT computation. J Phys Chem B 2021;125:601-11.
200. Jin H, Zhang H, Li J, et al. Discovery of novel two-dimensional photovoltaic materials accelerated by machine learning. J Phys Chem Lett 2020;11:3075-81.
201. Rajagopal A, Yao K, Jen AK. Toward perovskite solar cell commercialization: a perspective and research roadmap based on interfacial engineering. Adv Mater 2018;30:e1800455.
202. Li Z, Klein TR, Kim DH, et al. Scalable fabrication of perovskite solar cells. Nat Rev Mater 2018:3.
203. Zhou G, Chu W, Prezhdo OV. Structural deformation controls charge losses in MAPbI$$_3$$: unsupervised machine learning of nonadiabatic molecular dynamics. ACS Energy Lett 2020;5:1930-8.
205. Park H, Jun C. A simple and fast algorithm for K-medoids clustering. Expert Syst Appl 2009;36:3336-41.
206. Ertl P, Schuffenhauer A. Estimation of synthetic accessibility score of drug-like molecules based on molecular complexity and fragment contributions. J Cheminform 2009;1:8.
207. Venkatraman V, Yemene AE, de Mello J. Prediction of absorption spectrum shifts in dyes adsorbed on titania. Sci Rep 2019;9:16983.
208. Isida fragmentor. Available from: http://infochim.u-strasbg.fr/downloads/manuals/Fragmentor2017/Fragmentor2017_Manual_nov2017.pdf [Last accessed on 13 Jun 2022].
209. Cooper CB, Beard EJ, Vázquez-mayagoitia Á, et al. Design-to-device approach affords panchromatic co-sensitized solar cells. Adv Energy Mater 2019;9:1802820.
210. Swain MC, Cole JM. ChemDataExtractor: a toolkit for automated extraction of chemical information from the scientific literature. J Chem Inf Model 2016;56:1894-904.
211. Lee M. Insights from machine learning techniques for predicting the efficiency of fullerene derivatives-based ternary organic solar cells at ternary blend design. Adv Energy Mater 2019; doi: 10.1002/aenm.201900891.
212. Zhao Z, del Cueto M, Geng Y, Troisi A. Effect of increasing the descriptor set on machine learning prediction of small molecule-based organic solar cells. Chem Mater 2020;32:7777-87.
213. Meftahi N, Klymenko M, Christofferson AJ, Bach U, Winkler DA, Russo SP. Machine learning property prediction for organic photovoltaic devices. npj Comput Mater 2020:6.
214. Carbonell P, Carlsson L, Faulon JL. Stereo signature molecular descriptor. J Chem Inf Model 2013;53:887-97.
215. Scharber M, Mühlbacher D, Koppe M, et al. Design rules for donors in bulk-heterojunction solar cells-towards 10 % energy-conversion efficiency. Adv Mater 2006;18:789-94.
216. Winkler DA, Burden FR. Robust QSAR models from novel descriptors and bayesian regularised neural networks. Mol Simul 2006;24:243-58.
217. Lucic B, Amic D, Trinajstic N. Nonlinear multivariate regression outperforms several concisely designed neural networks on three QSPR data sets. J Chem Inf Comput Sci 2000;40:403-13.
218. David TW, Anizelli H, Jacobsson TJ, Gray C, Teahan W, Kettle J. Enhancing the stability of organic photovoltaics through machine learning. Nano Energy 2020;78:105342.
219. Reese MO, Gevorgyan SA, Jørgensen M, et al. Consensus stability testing protocols for organic photovoltaic materials and devices. Sol Energy Mater Sol Cells 2011;95:1253-67.
220. Flake GW, Lawrence S. Efficient SVM regression training with SMO. Machine Learning 2002;46:271-90.
221. Du X, Lüer L, Heumueller T, et al. Elucidating the full potential of OPV materials utilizing a high-throughput robot-based platform and machine learning. Joule 2021;5:495-506.
224. Lu T, Li H, Li M, Wang S, Lu W. Predicting experimental formability of hybrid organic-inorganic perovskites via imbalanced learning. J Phys Chem Lett 2022;13:3032-8.
225. Im J, Lee S, Ko T, Kim HW, Hyon Y, Chang H. Identifying Pb-free perovskites for solar cells by machine learning. npj Comput Mater 2019:5.
226. Sun S, Hartono NT, Ren ZD, et al. Accelerated development of perovskite-inspired materials via high-throughput synthesis and machine-learning diagnosis. Joule 2019;3:1437-51.
227. Lu S, Zhou Q, Ouyang Y, Guo Y, Li Q, Wang J. Accelerated discovery of stable lead-free hybrid organic-inorganic perovskites via machine learning. Nat Commun 2018;9:3405.
228. Li Z, Xu Q, Sun Q, Hou Z, Yin W. Thermodynamic stability landscape of halide double perovskites via high-throughput computing and machine learning. Adv Funct Mater 2019;29:1807280.
229. Schmidt J, Shi J, Borlido P, Chen L, Botti S, Marques MAL. Predicting the thermodynamic stability of solids combining density functional theory and machine learning. Chem Mater 2017;29:5090-103.
230. Venkatraman V, Foscato M, Jensen VR, Alsberg BK. Evolutionary de novo design of phenothiazine derivatives for dye-sensitized solar cells. J Mater Chem A 2015;3:9851-60.
231. Majeed N, Saladina M, Krompiec M, Greedy S, Deibel C, Mackenzie RCI. Using deep machine learning to understand the physical performance bottlenecks in novel thin-film solar cells. Adv Funct Mater 2020;30:1907259.
232. Pokuri BSS, Ghosal S, Kokate A, Sarkar S, Ganapathysubramanian B. Interpretable deep learning for guided microstructure-property explorations in photovoltaics. npj Comput Mater 2019:5.
233. Sahu H, Yang F, Ye X, Ma J, Fang W, Ma H. Designing promising molecules for organic solar cells via machine learning assisted virtual screening. J Mater Chem A 2019;7:17480-8.
234. Sahu H, Rao W, Troisi A, Ma H. Toward predicting efficiency of organic solar cells via machine learning and improved descriptors. Adv Energy Mater 2018;8:1801032.
235. Padula D, Troisi A. Concurrent optimization of organic donor-acceptor pairs through machine learning. Adv Energy Mater 2019;9:1902463.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Lu T, Li M, Lu W, Zhang TY. Recent progress in the data-driven discovery of novel photovoltaic materials. J Mater Inf 2022;2:7. http://dx.doi.org/10.20517/jmi.2022.07
AMA Style
Lu T, Li M, Lu W, Zhang TY. Recent progress in the data-driven discovery of novel photovoltaic materials. Journal of Materials Informatics. 2022; 2(2): 7. http://dx.doi.org/10.20517/jmi.2022.07
Chicago/Turabian Style
Lu, Tian, Minjie Li, Wencong Lu, Tong-Yi Zhang. 2022. "Recent progress in the data-driven discovery of novel photovoltaic materials" Journal of Materials Informatics. 2, no.2: 7. http://dx.doi.org/10.20517/jmi.2022.07
ACS Style
Lu, T.; Li M.; Lu W.; Zhang T.Y. Recent progress in the data-driven discovery of novel photovoltaic materials. J. Mater. Inf. 2022, 2, 7. http://dx.doi.org/10.20517/jmi.2022.07
About This Article
Copyright
Data & Comments
Data
 Cite This Article 29 clicks
Cite This Article 29 clicks


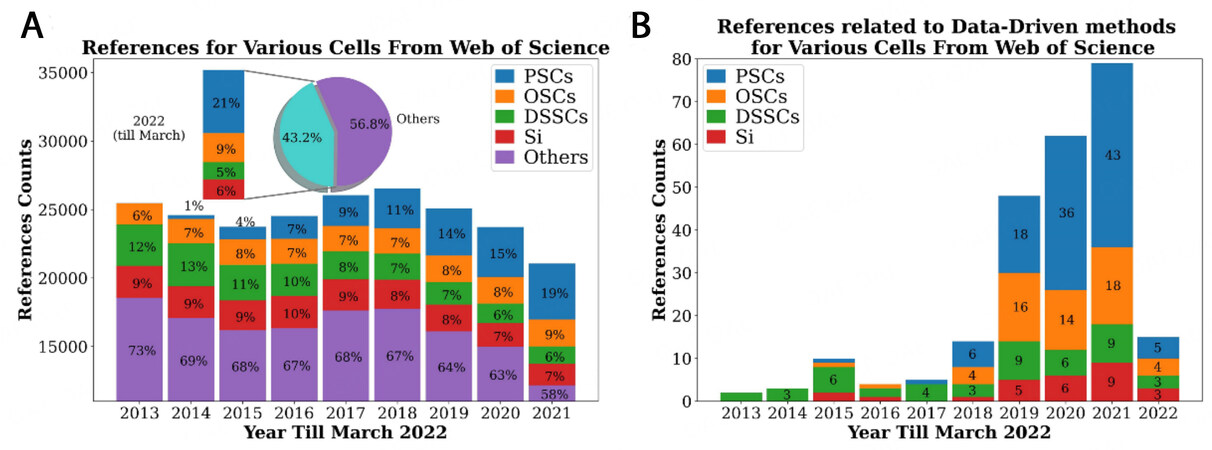
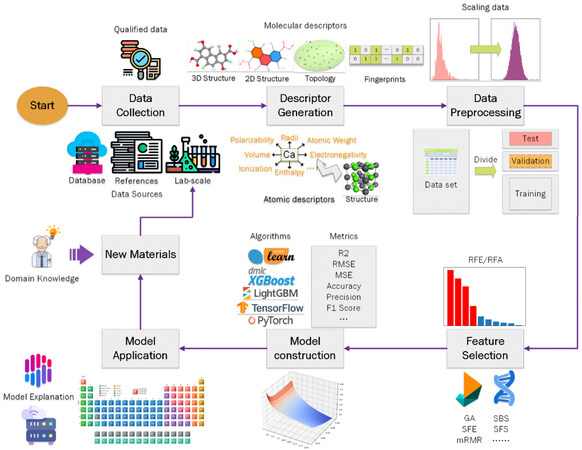
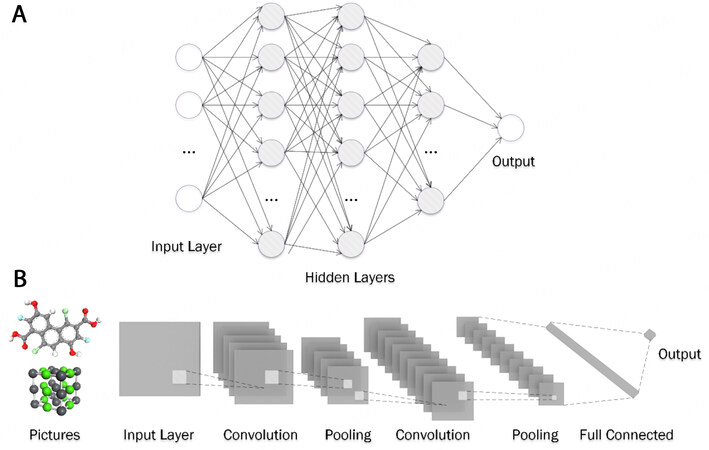
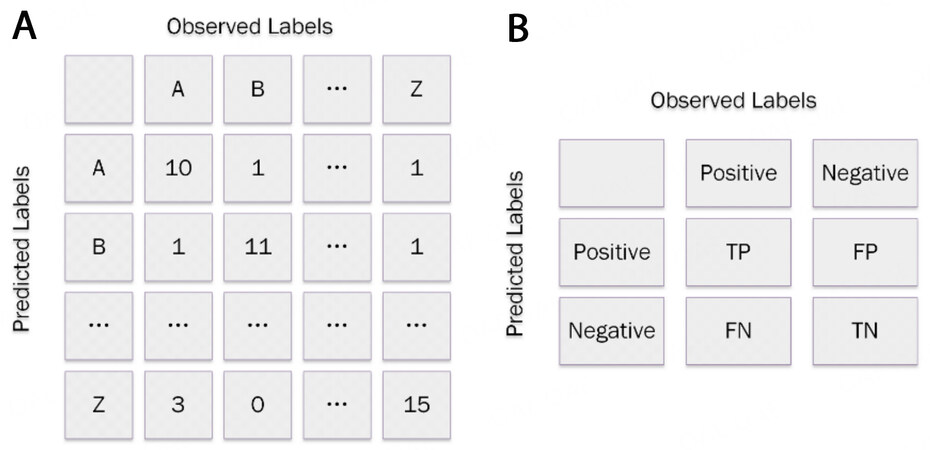
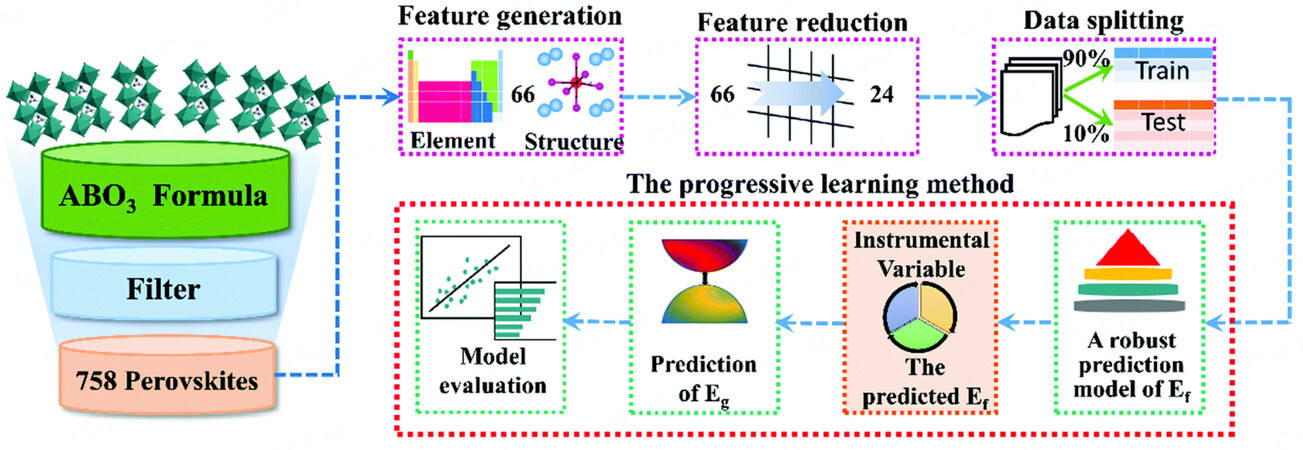
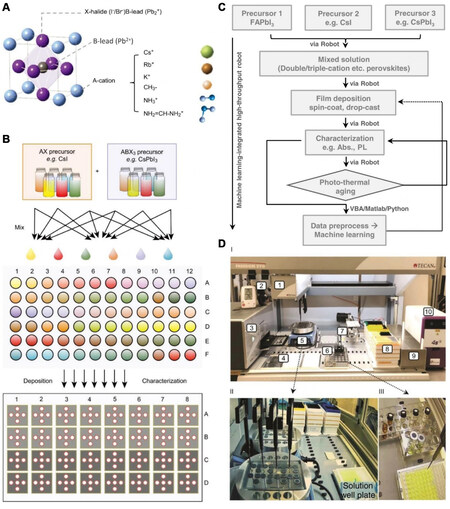
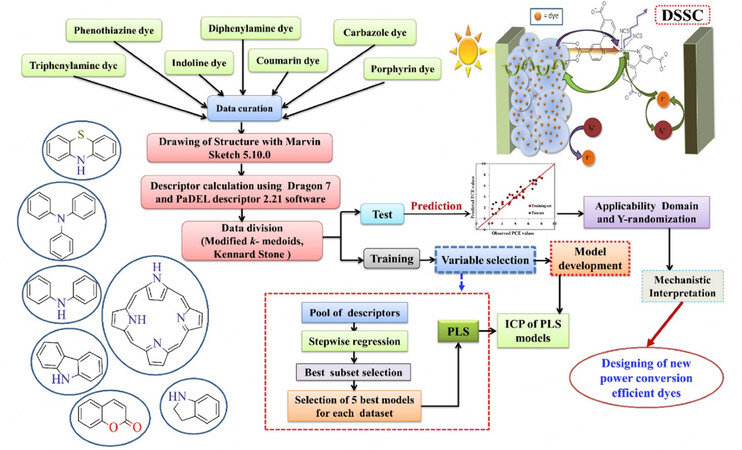










Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.