Taking materials dynamics to new extremes using machine learning interatomic potentials
Abstract
Understanding materials dynamics under extreme conditions of pressure, temperature, and strain rate is a scientific quest that spans nearly a century. Atomic simulations have had a considerable impact on this endeavor because of their ability to uncover materials’ microstructure evolution and properties at the scale of the relevant physical phenomena. However, this is still a challenge for most materials as it requires modeling large atomic systems (up to millions of particles) with improved accuracy. In many cases, the availability of sufficiently accurate but efficient interatomic potentials has become a serious bottleneck for performing these simulations as traditional potentials fail to represent the multitude of bonding. A new class of potentials has emerged recently, based on a different paradigm from the traditional approach. The new potentials are constructed by machine-learning with a high degree of fidelity from quantum-mechanical calculations. In this review, a brief introduction to the central ideas underlying machine learning interatomic potentials is given. In particular, the coupling of machine learning models with domain knowledge to improve accuracy, computational efficiency, and interpretability is highlighted. Subsequently, we demonstrate the effectiveness of the domain knowledge-based approach in certain select problems related to the kinetic response of warm dense materials. It is hoped that this review will inspire further advances in the understanding of matter under extreme conditions.
Keywords
Introduction
Materials exposed to extreme environments, e.g., small scales, high temperature, high pressure, or high strain rate, can undergo significant changes in their bonding, structures, and properties that induce new physical phenomena that do not occur under ordinary conditions[1-4]. Those extreme phenomena are central to many of the fascinating grand challenges of science, including behavior far from equilibrium, planetary dynamics, the evolution of stars, and the origin of life on Earth[5,6]. On the other hand, the need to develop materials that can perform well in severe operating environments also drives us to understand how the micro- and nano-structures evolve, such as crystallite size, dislocations, voids, and grain boundaries[7-11]. Researchers must not only observe and understand the behavior of materials under such extreme environments but also tailor and control a material’s response to enhance a device’s performance, extend its lifetime, or enable new technologies[12-16].
It is widely accepted that the material morphology and timescales of physical phenomena have a profound impact on the dynamics of the materials under extreme conditions. While the development of in-situ experimental investigations was unimaginable just a decade ago[17], the widespread applicability of these experimental methods is limited by the associated expenses and equipment needs. These methods also lack the temporal and spatial resolution needed to provide a real-time description of the physical quantities (stresses, density, temperature, etc.) and deformation phenomena (e.g., phase transformation, spall, etc.). Recent advancements in simulation capabilities greatly extend our tools for studying materials behavior over a wide range of spatial and temporal scales[18-21]. Atomistic computer simulations, which match the scale of the relevant physical phenomena - nanometers to micrometers and picoseconds to nanoseconds, can be especially valuable in gaining insights into the materials’ underlying structure and dynamics, driven by physical laws and chemical bonding[18,19]. For example, increasing molecular dynamics (MD) simulations on specific materials are helping to shed light on the atomic-scale understanding of how materials respond to extreme compression[22-27].
However, a challenge for atomistic simulations of most materials under extreme conditions continues to be achieving the optimal trade-off between computational accuracy and efficiency. So far, most computational simulations of high-accuracy or first-principles calculations have mainly focused on the thermodynamics and the crystal and electronic structures of systems involved[28,29]. For example, the phase stability and equation of state, which are determined by the corresponding Gibbs free energy, can be easily evaluated by first-principles calculations. Nevertheless, the microscopic kinetic response of materials and associated mechanisms (e.g., the transition pathway, transition barrier, etc.) of phase changes are often far from accessible due to a high computational cost via first-principles calculations, e.g., ab initio molecular dynamics is very expensive. More importantly, studying these processes remains a challenging task since their microstructural development involves the use of a large number of atoms[22,25] i.e., a high degree of configurational entropy. In addition, new phase or defect nucleation is a rare event that occurs over much longer timescales than can be achieved by ab initio molecular dynamics. Thus, it is necessary to resort to large-scale MD simulations using appropriate interatomic potentials. Although several orders of magnitude faster than first principle calculations, the classic semi-empirical potentials, i.e., which assume certain physical forms for the atomic interactions, are unable to describe the multitude of bonding that often exists and thus fail to reproduce materials dynamics faithfully at extremes.
Over the past decade, a class of machine learning (ML) based atomic simulation methods has emerged as a promising means to solve the aforementioned dilemma[30], combining the high accuracy of density functional theory (DFT) calculations and the computational high efficiency of MD simulations. The basic idea of ML potentials is to map local structural motifs onto the potential energy of the system by numerical interpolation between known reference quantum-mechanical calculations using a machine learning algorithm. This mapping is built in higher dimensional space, which is easier to cover the complex structural and bond evolution, beyond the limitation of given expressions. This scheme is quite different from the traditional potentials aimed at capturing the basic physics of interatomic bonding in materials[31-35]. Whereas several such prescriptions have been proposed for solids in the past, a complete description of warm dense materials places a higher demand on machine learning interatomic potentials (MLIPs). In the present work, we will review recent developments in MLIPs[36-42]. Attention will be paid to MLIPs that facilitate large-scale atomic simulations of materials dynamics under different external fields. We will show selected applications of ML potentials to problems in different types of materials, including transforming metals and alloys, ionic solids and liquids, molecular crystals and liquids and covalent bond materials. Finally, we include a summary that presents a perspective of the future of this field.
Machine learning potentials
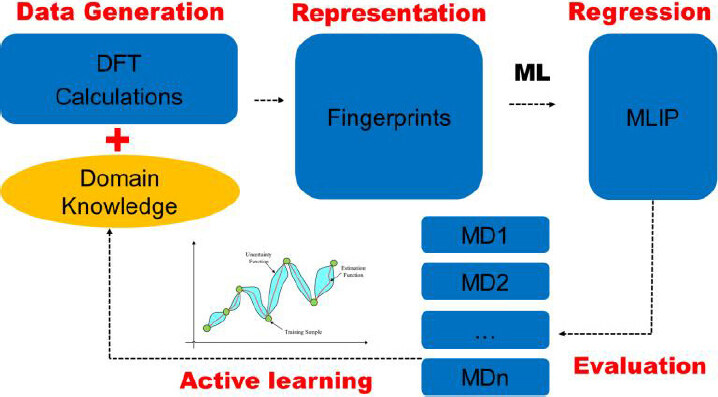
The aim of an MLIP is to map the configuration of a system in real space into its potential energy surface (PES). Based on a set of discrete points on PES (generated by DFT calculations), ML regression algorithms are applied to learn a smooth PES. We can then predict the potential energy E of a given configuration. The total force Fi acting on individual atom i in this system can be expressed as Fi = -∂E/∂ri, where ri is the position of atom i. MD simulations can be performed similarly to those with classical interatomic potentials. The general ingredients of MLIPs include the representation for local atomic environments, learning databases, regression models, and evaluation algorithms [Figure 1]. We will review these key aspects in this section.
Figure 1. The strategy of machine learning interatomic potential development. The main processes include data generation, feature representation, ML regression, and model evaluation. Active learning is used to update and optimize the performance of the best potential at any instant. DFT: Density functional theory; ML: machine learning.
Learning databases
Learning database involves the information of different structural configurations and the corresponding energies, forces, and stresses. The target energies (forces and/or stresses) are obtained by DFT calculations[28,29]. Therefore, a high-quality learning database should use limited configurations to capture the PES accurately. However, it is difficult to deal with the trade-off between accuracy and efficiency.
The most frequently used method to obtain a good database is to collect reference configurations that are most related to the specific applications. For example, a database including crystal defects such as vacancies, interstitials, dislocations, twin boundaries, and free surfaces is desirable for developing an MLIP to describe the mechanical behavior of metallic materials[43-46]. However, the ML potential learned from such a dataset may have poor predictions for other properties. Noticeably, the learning dataset collection will become extremely demanding when developing MLIP to study complex phase transformations in materials, which include structures under different conditions[40,47,48] e.g., temperature, pressure, etc.
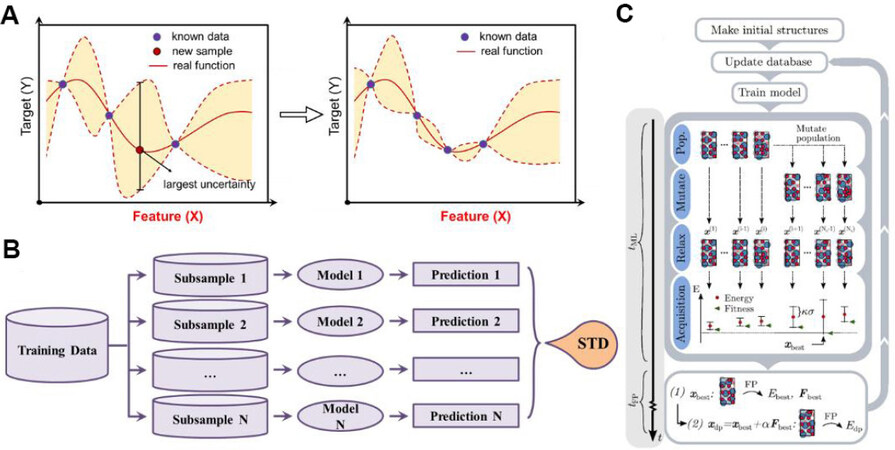
A highly efficient way to build the learning database is to collect reference data by active learning[49-52]. A feedback flow was integrated into the new reference selection[Figure 1]. In this scenario, a raw MLIP was first constructed by a small dataset, then MD simulations were run using this potential to generate more configurations. The configurations with high uncertainty are selected and then re-labeled by DFT calculations and updated the training dataset [Figure 2A]. Although it often takes several iterations to achieve the acceptable learning dataset, active learning can effectively reduce the size of the training dataset without loss of training accuracy. The most important process in active learning is re-sampling. However, most ML regression algorithms cannot provide the uncertainty directly. To solve this problem, random sampling methods (e.g., Bootstrapping) have been used to evaluate the uncertainty [Figure 2B]. Even so, not all important metastable structures can be sampled. Therefore, we often enrich the learning dataset with the help of some global optimization method[52], which can be more efficient in sampling metastable structures along the phase transition pathways [Figure 2C].
Figure 2. Typical strategies for efficiently sampling in active learning. (A) Based on algorithms e.g., Gaussian regression, density functional theory (DFT) calculations are usually applied on configurations with high uncertainty. (B) Uncertainty can also be evaluated by several parallel models; the standard derivation (STD) of N predictions reflects the uncertainty of selected configurations. (C) Global optimizations are also applied to select important structures for DFT calculations[52].
Representations for local atomic environments
Representation of atomic structures entails quantifying local structural information in certain mathematical expressions, named descriptors or fingerprints[53]. In order to simulate large systems, the total energy is expressed as a linear combination of the sum of local energy contributions from all the atoms. Similarly, the fingerprints can also be simplified as a linear summation of local atomic environments, i.e., D = ΣDi, where D is the fingerprints of the system, and Di is the fingerprint of atom i. This assumption greatly improves the efficiency of MLIPs[54,55].
The aim of Di is to reveal the local structural characteristics of atom i in feature space. In general, the descriptor Di should fulfill the symmetric requirement, namely, the invariance with symmetry operation such as translation and rotation. Nevertheless, there are still some tricky situations where different structures generate the same descriptors[56], which should be avoided as much as possible.
The selection of Di is of great importance as it can affect the accuracy and efficiency of MLIPs. Several different representations have been proposed in the past decade[53,56-65], including the Gaussian function truncated forms[66] and the spherical harmonic function[62].
Gaussian function based descriptors
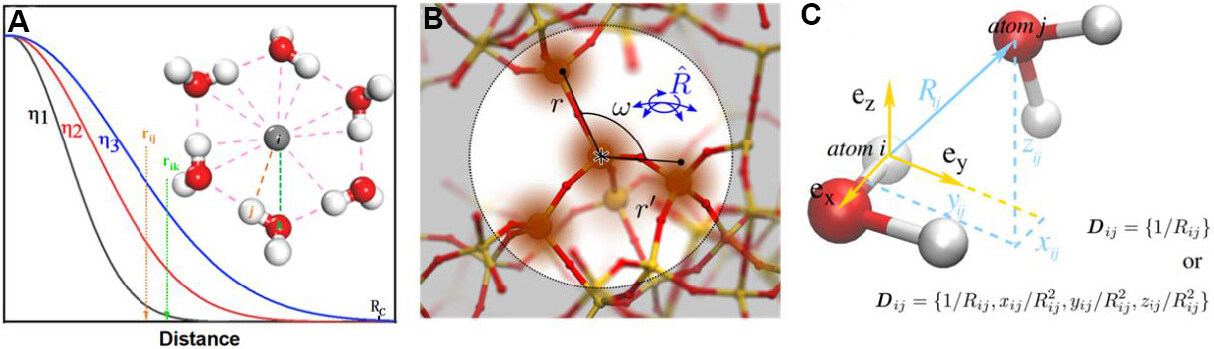
The core part of this type of descriptors is a Gaussian function smoothened by a cutoff function[66]. The cutoff function usually has the following form:
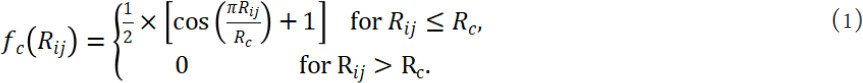
where Rij is the interatomic distance, Rc is the cutoff distance. The Gaussian function form can be two-body (focused on the bond length) or three-body (focused on the bond angle information). A typical two-body Gaussian function based descriptors can be:
where η and Rs are parameters to control the position and the width of the Gaussian function [Figure 3A]. The summation goes through all neighbor j of atom i within the Rc. The two-body Gaussian descriptors can be easily extended to three-body ones by introducing the angle θijk centered at atom i. A typical three-body Gaussian type descriptor can have the form of:
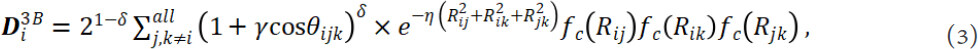
with the parameter γ (= +1, -1), η, and δ. The Gaussian function based structural descriptors is easy enough to ensure a high efficiency upon calculations. There are different functional forms[30,58,66-68] that have equal efficiency.
Spherical harmonic function based descriptors
Expanding the Gaussian representation of neighbor information by spherical harmonic functions is the central idea for this type of descriptors [Figure 3B]. Typical formats include smooth overlap of atomic positions descriptors[57,69], spectral neighbor analysis potential (SNAP) descriptors[70] and atomic cluster expansion descriptors[59]. More detailed theoretical analysis of these descriptors can be found in the references.
A particularly simple descriptor was adopted by deep potential molecular dynamics (DPMD)[71], as shown in Figure 3C. DPMD has shown good applicability to many kinds of materials[72-75] because the DeepPotSE descriptors[76] adopted by DPMD are no longer limited to fixed expression but are automatically learned through neural network thanks to the well-designed symmetry invariant function:
where Di is the descriptor matrix of atom i;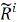 
is the generalized local environment matrix constructed by the function of relative position between the central atom i and each local environment atom, gi1 and gi2 are embedding matrix learned by the neural network according to the weighting function smoothly going to zero at the boundary of the local region.
Despite the great success of the abovementioned descriptors in MLIPs, the construction of efficient fingerprints for systems with complex structures, which often emerge under extreme conditions, remains difficult. An alternative strategy to design structural descriptors is to combine the functions with proper domain knowledge, which is an efficient way to describe the materials with complex structures. Using domain knowledge screened descriptors, sensitive to the structural changes can help to solve the tradeoff between complexity and efficiency. For example, Zong et al.[25,67] use lattice-invariant shear based descriptors for the phase transformations in Zr and predict a new phase mediating the shock-induced phase transition. In addition, they use physical model based descriptors that can describe up to 14 different structures in K[77,78]. Also, domain knowledge can be coupled with angle dependent structural descriptors, successfully capturing the change of chemical bond in solid H2[79].
It is not easy to evaluate the quality of descriptors because descriptors are not the only factor that can affect the performance of MLIPs. However, the sensitivity of descriptors to the perturbation of specific structures is a good choice to validate its application range. Onat et al.[53] used four different databases to evaluate the sensitivity of eight different descriptors, which can be accessed in reference.
Regression models
A regression model is needed to map the high-dimensional fingerprints onto the corresponding PES. The prevailing regression algorithms include linear regression, kernel function based regression, and artificial neural network (NN) regression.
Linear regression
The linear regression algorithm is the simplest method to obtain fitting parameters, which are determined by using weighted least-squares linear regression against the full training database, as shown,
where ω is the learned weight factor. Among them, the most widely used MLIPs include spectral neighbor analysis potential[70] and moment tensor potentials[65,80]. However, the performance of a linear regression model often lacks transferability. To resolve this issue, high-quality descriptors are desired to capture the nonlinear relationship between local structures and energy (force and/or stress).
Neural network regression
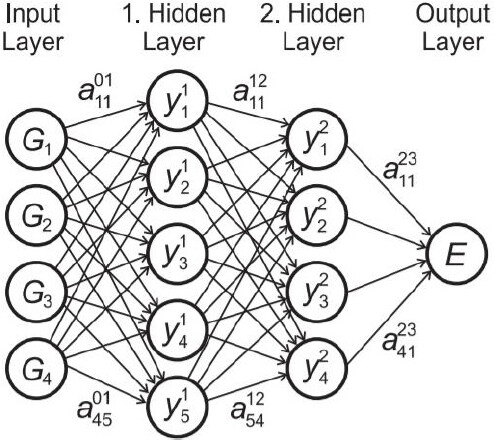
Artificial NN regression has excellent generalization ability and has flexible requirements[36,46,66,68,71,81-107]. A typical frame is illustrated in Figure 4[89]. The input and output of a NN model are descriptors Di and energy E, respectively. The complex network structures will find the implicit nonlinear relationship between Di and E. Since the relationship between atomic positions R and Di is constructed artificially, the total energy E can be connected to R. Despite a direct prediction of energy E, Pun et al.[68] proposed a new method of physically informed artificial neural networks (PINN) to generate interatomic potentials. Instead of energy E, parameters in a given physical model become the target in this NN. The PINN model can drastically improve the transferability of ML potentials by informing them of the physical nature of interatomic bonding[68]. Parameterizing a NN regression model needs a relatively large training dataset, which is too time-consuming for DFT calculations.
Figure 4. Structure of a feed-forward neural network[89].
Kernel based regression
The basic idea underlying kernel based regressions is to train the regression model in the kernel space, which is a higher dimensional feature space[108,109]. A kernel function K(D) is used to transform the descriptors from the feature space into the kernel space[110]. The common kernel based regression contains Gaussian process regression[111] and kernel ridge regression (KRR)[67]. Taking KRR as an example, a kernel function is introduced into the ridge regression method. The applied kernel function K(Dinput, Dref) measures the distance between the input descriptor Dinput and the reference descriptor Dref. Based on this, the final expression of potential energy is:
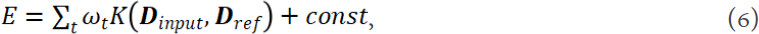
Where ωt are the learned weight factor.
Performance evaluation
MLIPs should be comprehensively evaluated before we achieve a reliable potential that can be used to perform further atomic simulations. The evaluation should be divided into two parts: the general performance of the ML model and the prediction of interested physical properties.
The precision of the ML model can be estimated by the root mean square error (RMSE) or the mean absolute error. Generally speaking, an RMSE of the potential energy is usually smaller than 5 meV/atom, while the RMSE of force is about 0.1 eV/Å[67]. In addition, n-fold cross validation is often used to avoid the possible overfitting problem. This is particularly important as the potential has to capture more than one interested property.
The evaluation of the performance of the learned potential in MD simulations depends on the interested properties. For example, stable structure prediction at given temperature and pressures is important for phase-diagram prediction[25,77,78], while dislocation core structure, generalized stacking fault energy prediction is important for mechanical properties[46,102]; accurate phonon spectra are indispensable for the prediction of thermal conductivity[112].
Applications of MLIPs to materials in extremes
Transforming metals and alloys
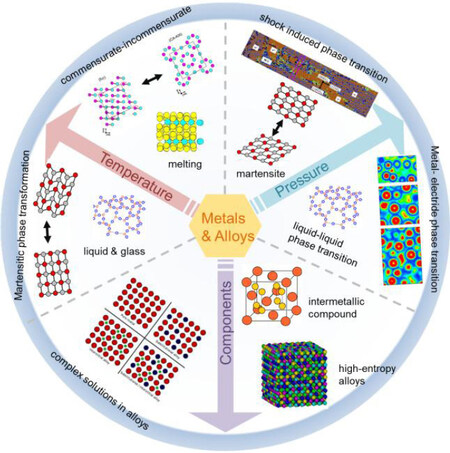
Metallic materials show complex material response as a function of chemical composition, temperature, and pressure, etc.[Figure 5][113-115]. Atomistic simulations provide powerful tools to study their atom-level processes with standard interatomic potentials, e.g., embedded atom method (EAM) and modified embedded atom methods, both of which have been successful in describing the mechanical behavior of metals and their alloys. However, these physical models based classical interatomic potentials still fail to represent the multitude of bonding in metallic materials that suffer from phase changes or plastic deformation in response to extremely loading or heating.
Figure 5. Complex material dynamics in metals and alloys under extreme conditions of high temperature, high pressure, and various components. At high temperature, metallic materials can show rich structural phase transformations e.g., martensite phase transformation[67], glass transition[113], melting[47,114], incommensurate transition[115], etc. While at high pressure, new states of matter via structural phase transformation, metal-electride transition[78], and liquid-liquid phase transition may be achieved. The increase of components leads to the formation of complex solid-solutions, clusters, segregations, intermetallic compounds, and short-range-ordered high entropy alloys.
ML interatomic potentials shed some light on these issues as they can accurately predict the atom-level properties of metallic materials over a wide range of temperatures and pressures. The reported ML potentials show success in W[116], Cu[117], Ti[70], Al[118], Fe[119,120], Zr[67], Mg[102], K[77,78], CuZr[107], MgCa[121], and AlCu[46], etc. For example, a NN potential for Fe developed by Maillet et al.[120] predict both elastic-plastic behavior and phase transitions over the entire range of pressures. A full temperature-pressure phase diagram for Zr is produced by Zong et al.[67] via ML potential based MD simulations. No classical potentials i.e., EAM or MEAM, can depict the pressure induced hcp-ω phase transition. Based on the ML potential, the authors investigated the shock-induced phase transformations in Zr, which helps to clarify the longstanding controversy over the phase transformation pathways. Potassium (K) possesses a more complex phase transformation behavior with fourteen different phases in the temperature-pressure phase diagram. Combining ML models with DFT calculations, the constructed ML potential reproduces the complex phase diagram, and predicts the commensurate-incommensurate phase transformation[115], semi-melting phase transformations[77], and metal-electride phase transition[78] in potassium, which are difficult to describe by classical interatomic potentials.
Atomic simulation of complex multi-component alloys is another challenge for metallic materials. Luckily, ML potential also performs well in capturing these alloy systems of binary or ternary components[46,96,107,121,122]. Also, many intermetallic compounds have been studied with the help of MLIPs, such as TiO2[95], HfO2[73,123], ZnO[124], etc. Interestingly, Sivaraman et al.[125] developed a new approach to develop ML potentials, which are directly machine learned from experimental measurements, and successfully describe the multi-phase state of refractory oxides. Multi-component concentrated solid solutions are successful examples for ML potentials related to alloying effects[122]. Kobayashi et al.[97] and Jain et al.[126] developed a ternary ML potential for Al-Mg-Si alloys, which exactly reproduces the heat of solution, solute-solute, and solute-vacancy interaction energies, and formation energies of small solute clusters and precipitates. Our previous work also reported the ability of MLIP in describing complex dislocation core structures in high-strain-rate deformed or shock compressed bcc high entropy alloys[127].
Ionic crystals and liquids
Different from metallic materials, the interaction between atoms in an ionic crystal is controlled by Coulomb bonding, which is a long-range force field. As a function of the ratio between the anionic-cationic radius, ionic materials can show crystal structures from simple e.g., NaCl or CsCl to complex ones e.g., perovskite and rutile. Several physical models based semi-empirical potentials have been used to describe the dynamic properties of these ionic crystal materials. However, these semi-empirical formulas are out of reach in studying disordered ionic liquids or molten salts, which are important for developing new types of clean energy materials, such as molten salt reactors and concentrated solar power technology.
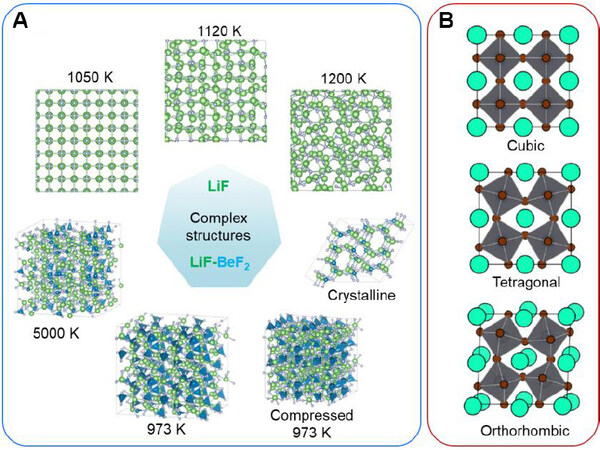
Li et al.[128] developed a robust neural network interatomic potential model for molten salts such as NaCl, LiF, and FLiBe[129]. In their machine learning model, both long-rang and short-range interactions are captured for both ionic crystals and liquids. More importantly, these NN interatomic potentials have high accuracy in calculating the structural, thermophysical, and transport properties but are 1000 times faster than first principle methods. Figure 6A shows the NN interatomic potential based MD simulation of complex structural phase transformation behavior in LiF and Flipe (LiF-BeF2 mixtures). The NN interatomic potential accurately reproduced the ab initio interactions of dimers, crystalline solids under deformation, crystalline LiF near the melting point, and liquid LiF at high temperatures. These applications suggest a paradigm shift from empirical/semi-empirical/abinitio approaches to an efficient and accurate machine learning scheme in molten salt modeling.
Perovskites are another typical ionic crystal ceramics with extensive applications in memory, solar cells, and transistors, etc. However, the development of corresponding interatomic potentials is still full of thorns due to the presence of rich and complicated polymorphism. Taking CsPbBr3 as an example in Figure 6B, there exit complex structural phase transformations, during which the symmetry breaking does not only occur at the lattice level but also at the sub-lattice level, e.g., tetrahedral rotations. Thomas and collaborators developed an ML potential for CsPbBr3[48], which shows similar accuracy but higher efficiency than DFT calculations. Such ML potentials enable MD simulations to take into account the contribution of inharmonic Hamiltonians during the phase transformation. More strikingly, the integration of ML potential in the processes of predicting or searching stable chemical compositions can greatly accelerate the discovery of new perovskite materials with novel functional properties.
Molecular crystals and liquids
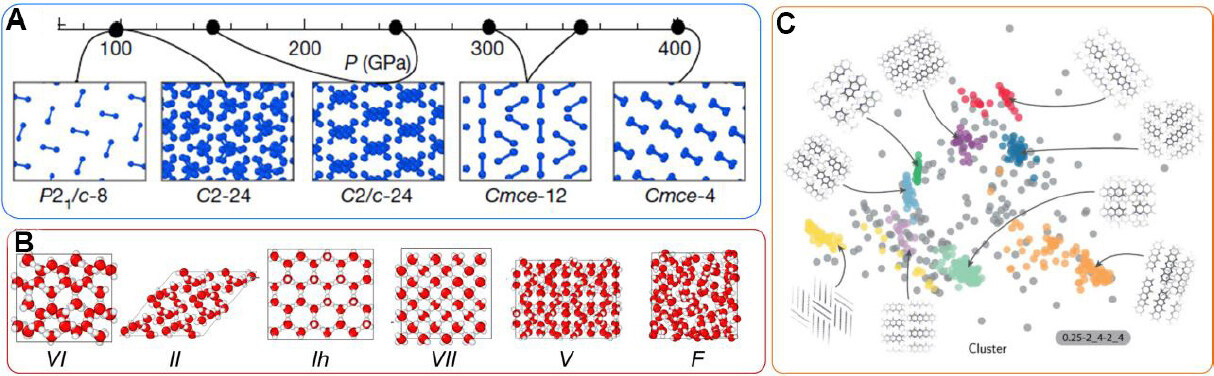
Molecular crystal materials possess complex bonding, including inter-molecular and intra-molecular bond types. In general, inter-molecular bonds are weak van der Waals interactions while the intra-molecular bonds are strongly covalent, and the dynamics of materials in molecular crystals are closely related to the bond breaking and forming process. Although reactive force field (ReaxFF)[130] potentials show good performance in the atomic simulation of molecular crystal systems, it is still difficult to fulfill the demand for describing the rich conformational changes in molecular systems under extreme conditions. Figure 7A shows the complex structural changes in hydrogen as a function of pressure[131]. The rich structures of H2O at different temperatures and pressures are shown in Figure 7B[75]. In organic systems e.g., Azapentacene 5A[132], the polymorphs are also very complex [Figure 7C]. Still lacking is the microscopic measurement of phase transformation dynamics for molecular crystal materials, even though the possible structure of stable phases has been largely solved by DFT calculations.
With the help of ML potentials, large-scale MD simulations become a powerful tool to understand small molecular crystal systems. The complex structural dynamics of H2[79,131], H2O[75], C60[133] and Azapentacene[132] have been investigated recently. Taking hydrogen as an example, we review the power of MLIP in investigating phase transformation in high-density molecular systems. Zong et al.[79] and Cheng et al.[131] developed MLIPs for hydrogen separately almost at the same time. Cheng et al.[131] reproduce both the reentrant melting behavior and the polymorphism of the solid phase. They prove a continuous molecular-to-atomic transition in the liquid, with no first-order transition observed above the melting line, which suggests a smooth transition between insulating and metallic layers in giant gas planets, and reconciles existing discrepancies between experiments as a manifestation of supercritical behavior. Zong et al.[79] get an accurate potential to describe the complex Phase I, II, III and liquid phase of hydrogen. Phase I shows a typical hcp lattice of the molecular centers while the orientation of the H2 molecular is disordered and remains rotating freely. The inter-molecular interactions are mainly from the quadrupole-quadrupole interactions and steric repulsion. With increasing pressure (> 100 GPa), steric repulsion becomes the most important driving force for molecular reorientation, inducing a denser liquid phase than solid. H2 molecules in Phase II have an ordered molecular axis orientation, and the lattice is more likely to be P21/c-24. The details of Phase III need to be further investigated because the present potential cannot fully describe the bond breaking events under high pressure. These results deepen our understanding of the solid polymorphism and anomalous melting behavior in hydrogen and show the potential of MLIPs in providing an understanding of molecular systems in extremes.
Covalent bond crystals and amorphous
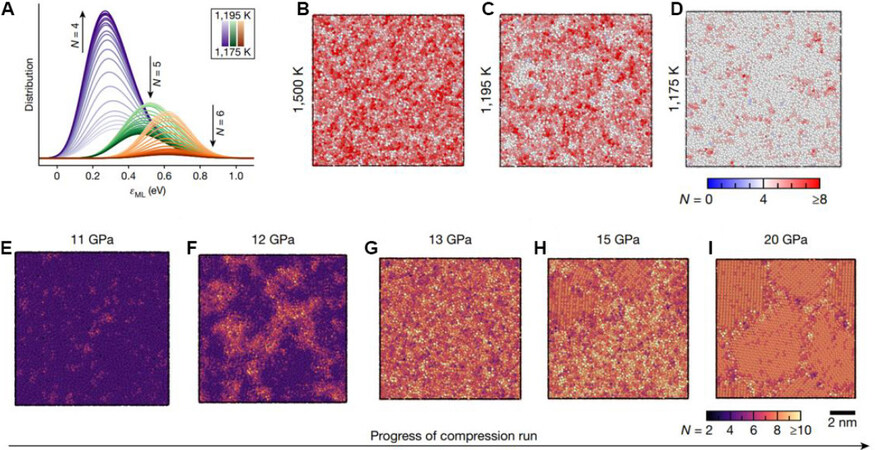
ML interatomic potentials have been applied successfully to many covalent bonded materials, e.g., carbon[134-136], silicon[137-139], silica[140] and Si-H system[141], phosphorus[142], gallium[143], phase change materials GeTe[92], Ge2Sb2Te5[144] and 2D ferroic GeSe[145], etc. With the help of MLIPs, there is a much clearer picture of structural changes in covalent-bonded liquids and solids under high pressure. For example, Deringer et al.[139] performed MD simulations to study the complex phase transformations in disordered silicon, including the liquid-amorphous phase transformations and amorphous-amorphous phase transformations under compression. They first created an MLIP that can accurately describe the liquid-amorphous transition upon quenching at a cooling rate of 1011 K/s [Figure 8A-D]. After applying external pressure, the amorphous silicon is gradually crystallized in a three-step transformation pathway. At 11 GPa, a coexisting state of low-density amorphous and high-density amorphous is observed [Figure 8E-F]. Further increasing the pressure to 13 GPa gives rise to a very high-density amorphous phase [Figure 8G], which is followed by full crystallization [Figure 8H-I]. This work demonstrates the feasibility of data-driven atomic simulation approaches in uncovering the complex material behavior of covalent-bonded systems.
Figure 8. Liquid-amorphous transformation and a three-step crystallization in amorphous Si[139]. (A) Coordinate number distribution upon quenching. (B-D) Typical atomic configurations of liquid-amorphous transformation upon quenching. (E-I) Typical atomic configurations of a three-step crystallization.
Limitation of present MLIPs and possible solutions
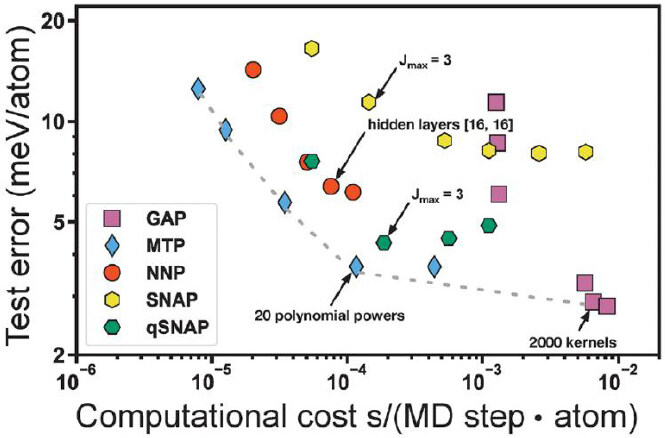
Machine learning interatomic potentials have emerged as a powerful new tool for atomic modeling materials in extremes. A strategy combining domain knowledge with a machine learning model can greatly accelerate the development of interatomic potentials and improve their accuracy. Zuo et al.[63] compared the test error of main MLIPs, including Gaussian approximation potential, moment tensor potential, neural network potential, SNAP, and quadratic spectral neighbor analysis potential, etc. as functions of the computational cost of bcc Mo, as shown in Figure 9. Obviously, potentials generated from different features have different performances. In general, MLIPs based MD simulations are ~ 100 times slower than classical ones, although the accuracy is much higher. However, the increase of the complexity, e.g., complex phase transitions and complex compositions etc., leads to more complex descriptors, which will burden the computational efficiency. Hajibabaei et al.[146,147] explored sparse Gaussian process regression to balance this trade-off. The key idea is to get a low-rank approximation of the covariance matrices upon calculating the kernel functions between the test configurations and the reference configurations. In this way, phase transitions of large and complex systems can be accessible.
Figure 9. Evolution of test error as functions of computational cost for Gaussian approximation potential (GAP), moment tensor potential (MTP), neural network potential (NNP), spectral neighbor analysis potential (SNAP), and quadratic spectral neighbor analysis potential (qSNAP) for bcc Mo[63].
Despite the high computational cost of complex structural descriptors, the designing of descriptors usually requires rich experiences for developers. In other words, the designing strategies of descriptors for different materials are usually not transferable, although almost all MLIPs are based on the same assumption: the potential energy of an atom only relates to its local structural environment (usually less than 1 nm), which is also the basis for the designing of structural descriptors. This assumption is acceptable in metals; however, the cutoff distance is too short for some long-range interactions, e.g., Coulomb force and van der Waals interactions, in ionic and molecular crystals. Although there have been some attempts[104,148-150] considering long-range interactions, the key issue has not been solved. In a word, the lack of transferability and the lack of description of long-range interaction remain the main challenge of MLIPs.
From our perspective, graph neural network (GNN)[151] based MLIPs show promise in addressing these issues about transferability and long-range interaction. In GNN, the topological structure of materials can be expressed by “nodes” and “edges” in a graph. One can easily describe the atoms using “nodes” and chemical bonds using “edges”. Therefore, the structural characters are not expressed by some special and semi-empirical formulas. With this end-to-end model, GNN based MLIPs can be transferred to any system easily. It should be noted that not only the explicit interactions between atoms (e.g., the chemical bonding and the interaction within a short-range cutoff), but also the implicit connection (long-range interactions) are described in a graph by the message passing between sub-graphs in GNN.
Conclusions
In summary, we reviewed the essential aspects of how to develop a machine learning interatomic potential and illustrated how such potentials have been applied in describing the dynamic/kinetics of different materials during structural transformations under extreme conditions. Machine learning interatomic potentials bridges accurate density functional theory calculations to quantitative multiscale simulations covering various time- and length-scales. This provides a good example for the realization of cross-scale computational materials science. We also discussed the limitations of the present MLIPs and gave our outlooks. We hope our review work could inspire and attract more attention in this research direction.
Declarations
Authors’ contributionsDesigned this project: Ding X, Zong H
Contributed to the review paper writing: Yang Y, Zhao L, Han CX, Ding SD, Lookman T, Sun J, Zong HX
Availability of data and materialsNot applicable.
Financial support and sponsorshipThis work was supported by Key Technologies R&D Program (2017YFB0702401), the National Natural Science Foundation of China (51320105014, 51871177 and 51931004) and the 111 project 2.0 (BP2018008).
Conflicts of interestAll authors declared that there are no conflicts of interest.
Ethical approval and consent to participateNot applicable.
Consent for publicationNot applicable.
Copyright© The Author(s) 2021.
REFERENCES
1. Asay JR, Shahinpoor M. High-pressure shock compression of solids. New York: Springer Science & Business Media; 2012.
2. Drickamer HG, Frank CW. Electronic transitions and the high pressure chemistry and physics of solids. New York: Springer Science & Business Media; 2013.
3. Graham RA. Solids under high-pressure shock compression: mechanics, physics, and chemistry. New York: Springer Science & Business Media; 2012.
4. Woollam JA, Chu CW. High-pressure and low-temperature physics. New York: Springer Science & Business Media; 2012.
5. Konôpková Z, McWilliams RS, Gómez-Pérez N, Goncharov AF. Direct measurement of thermal conductivity in solid iron at planetary core conditions. Nature 2016;534:99-101.
6. Monnereau M, Calvet M, Margerin L, Souriau A. Lopsided growth of Earth’s inner core. Science 2010;328:1014-7.
8. Wenk HR, Matthies S, Hemley RJ, Mao HK, Shu J. The plastic deformation of iron at pressures of the Earth’s inner core. Nature 2000;405:1044-7.
9. Valiev R. Nanostructuring of metals by severe plastic deformation for advanced properties. Nat Mater 2004;3:511-6.
10. Yu Q, Shan ZW, Li J, et al. Strong crystal size effect on deformation twinning. Nature 2010;463:335-8.
11. Zhou X, Feng Z, Zhu L, et al. High-pressure strengthening in ultrafine-grained metals. Nature 2020;579:67-72.
12. Aoyama T, Yamauchi K, Iyama A, Picozzi S, Shimizu K, Kimura T. Giant spin-driven ferroelectric polarization in TbMnO3 under high pressure. Nat Commun 2014;5:4927.
13. Cao Y, Fatemi V, Demir A, et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 2018;556:80-4.
14. Cao Y, Fatemi V, Fang S, et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018;556:43-50.
15. Zhao J, Gao J, Li W, et al. A combinatory ferroelectric compound bridging simple ABO3 and A-site-ordered quadruple perovskite. Nat Commun 2021;12:747.
16. Tan C, Dong Z, Li Y, et al. A high performance wearable strain sensor with advanced thermal management for motion monitoring. Nat Commun 2020;11:3530.
17. Tsiklis DS. Handbook of techniques in high-pressure research and engineering. New York: Springer Science & Business Media; 2012.
18. Andreoni W, Yip S. Handbook of materials modeling: methods: theory and modeling. Springer International Publishing; 2019.
19. Andreoni W, Yip S. Handbook of materials modeling: applications: current and emerging materials. Springer; 2020.
20. Collins LA, Boehly TR, Ding YH, et al. A review on ab initio studies of static, transport, and optical properties of polystyrene under extreme conditions for inertial confinement fusion applications. Physics of Plasmas 2018;25:056306.
21. Lees AW, Edwards SF. The computer study of transport processes under extreme conditions. J Phys C: Solid State Phys 1972;5:1921-8.
22. Nisoli C, Zong H, Niezgoda SR, Brown DW, Lookman T. Long-time behavior of the ω→’α transition in shocked zirconium: Interplay of nucleation and plastic deformation. Acta Materialia 2016;108:138-42.
23. Zong H, Ding X, Lookman T, et al. Collective nature of plasticity in mediating phase transformation under shock compression. Phys Rev B 2014:89.
24. Zong H, Ding X, Lookman T, Sun J. Twin boundary activated α→’ω phase transformation in titanium under shock compression. Acta Materialia 2016;115:1-9.
25. Zong H, He P, Ding X, Ackland GJ. Nucleation mechanism for hcp→’bcc phase transformation in shock-compressed Zr. Phys Rev B 2020;101:144105.
26. Zong H, Lookman T, Ding X, et al. The kinetics of the ω to α phase transformation in Zr, Ti: analysis of data from shock-recovered samples and atomistic simulations. Acta Materialia 2014;77:191-9.
27. Zong H, Luo Y, Ding X, Lookman T, Ackland GJ. hcp→’ω phase transition mechanisms in shocked zirconium: A machine learning based atomic simulation study. Acta Materialia 2019;162:126-35.
29. Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys Rev 1965;140:A1133-8.
30. Botu V, Batra R, Chapman J, Ramprasad R. Machine learning force fields: construction, validation, and outlook. J Phys Chem C 2017;121:511-22.
31. Daw MS, Baskes MI. Embedded-atom method: derivation and application to impurities, surfaces, and other defects in metals. Phys Rev B 1984;29:6443-53.
32. Finnis MW, Sinclair JE. A simple empirical N-body potential for transition metals. Philosophical Magazine A 2006;50:45-55.
33. Stillinger FH, Weber TA. Computer simulation of local order in condensed phases of silicon. Phys Rev B Condens Matter 1985;31:5262-71.
34. Tersoff J. New empirical approach for the structure and energy of covalent systems. Phys Rev B Condens Matter 1988;37:6991-7000.
35. Tersoff J. Empirical interatomic potential for silicon with improved elastic properties. Phys Rev B Condens Matter 1988;38:9902-5.
36. Blank TB, Brown SD, Calhoun AW, Doren DJ. Neural network models of potential energy surfaces. J Chem Phys 1995;103:4129-37.
37. de Pablo JJ, Jackson NE, Webb MA, et al. New frontiers for the materials genome initiative. npj Comput Mater 2019;5:1-23.
38. Deringer VL, Caro MA, Csányi G. Machine learning interatomic potentials as emerging tools for materials science. Adv Mater 2019;31:e1902765.
39. Ong SP. Accelerating materials science with high-throughput computations and machine learning. Comput Mater Sci 2019;161:143-50.
40. Rosenbrock CW, Gubaev K, Shapeev AV, et al. Machine-learned interatomic potentials for alloys and alloy phase diagrams. npj Comput Mater 2021;7:1-9.
41. Friederich P, Häse F, Proppe J, Aspuru-Guzik A. Machine-learned potentials for next-generation matter simulations. Nat Mater 2021;20:750-61.
42. Mishin Y. Machine-learning interatomic potentials for materials science. Acta Materialia 2021;214:116980.
43. Chen C, Deng Z, Tran R, Tang H, Chu I, Ong SP. Accurate force field for molybdenum by machine learning large materials data. Phys Rev Materials 2017;1:043603.
44. Byggmästar J, Hamedani A, Nordlund K, Djurabekova F. Machine-learning interatomic potential for radiation damage and defects in tungsten. Phys Rev B 2019:100.
45. Zeni C, Rossi K, Glielmo A, Baletto F. On machine learning force fields for metallic nanoparticles. Adv Phys X 2019;4:1654919.
46. Marchand D, Jain A, Glensk A, Curtin WA. Machine learning for metallurgy I. A neural-network potential for Al-Cu. Phys Rev Materials 2020;4:103601.
47. Jinnouchi R, Karsai F, Kresse G. On-the-fly machine learning force field generation: application to melting points. Phys Rev B 2019;100:014105.
48. Thomas JC, Bechtel JS, Natarajan AR, Van der Ven A. Machine learning the density functional theory potential energy surface for the inorganic halide perovskite CsPbBr3. Phys Rev B 2019;100:134101.
49. Podryabinkin EV, Shapeev AV. Active learning of linearly parametrized interatomic potentials. Comput Mater Sci 2017;140:171-80.
50. Gubaev K, Podryabinkin EV, Hart GL, Shapeev AV. Accelerating high-throughput searches for new alloys with active learning of interatomic potentials. Comput Mater Sci 2019;156:148-56.
51. Zhang L, Lin D, Wang H, Car R, Weinan E. Active learning of uniformly accurate interatomic potentials for materials simulation. Phys Rev Materials 2019;3:023804.
52. Bisbo MK, Hammer B. Efficient global structure optimization with a machine-learned surrogate model. Phys Rev Lett 2020;124:086102.
53. Onat B, Ortner C, Kermode JR. Sensitivity and dimensionality of atomic environment representations used for machine learning interatomic potentials. J Chem Phys 2020;153:144106.
54. Botu V, Ramprasad R. Adaptive machine learning framework to accelerate ab initio molecular dynamics. Int J Quantum Chem 2015;115:1074-83.
55. Botu V, Ramprasad R. Learning scheme to predict atomic forces and accelerate materials simulations. Phys Rev B 2015;92:094306.
56. Pozdnyakov SN, Willatt MJ, Bartók AP, Ortner C, Csányi G, Ceriotti M. Incompleteness of atomic structure representations. Phys Rev Lett 2020;125:166001.
58. Batra R, Tran HD, Kim C, et al. General atomic neighborhood fingerprint for machine learning-based methods. J Phys Chem C 2019;123:15859-66.
59. Drautz R. Atomic cluster expansion for accurate and transferable interatomic potentials. Phys Rev B 2019;99:014104.
60. Willatt MJ, Musil F, Ceriotti M. Atom-density representations for machine learning. J Chem Phys 2019;150:154110.
61. Himanen L, Jäger MO, Morooka EV, et al. DScribe: library of descriptors for machine learning in materials science. Comput Phys Commun 2020;247:106949.
62. Kocer E, Mason JK, Erturk H. Continuous and optimally complete description of chemical environments using Spherical Bessel descriptors. AIP Advances 2020;10:015021.
63. Zuo Y, Chen C, Li X, et al. Performance and cost assessment of machine learning interatomic potentials. J Phys Chem A 2020;124:731-45.
64. Novotni M, Klein R. Shape retrieval using 3D Zernike descriptors. Computer-Aided Design 2004;36:1047-62.
65. Shapeev AV. Moment tensor potentials: a class of systematically improvable interatomic potentials. Multiscale Model Simul 2016;14:1153-73.
66. Behler J, Parrinello M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys Rev Lett 2007;98:146401.
67. Zong H, Pilania G, Ding X, Ackland GJ, Lookman T. Developing an interatomic potential for martensitic phase transformations in zirconium by machine learning. npj Comput Mater 2018;4:1-8.
68. Pun GPP, Batra R, Ramprasad R, Mishin Y. Physically informed artificial neural networks for atomistic modeling of materials. Nat Commun 2019;10:2339.
69. Helfrecht BA, Semino R, Pireddu G, Auerbach SM, Ceriotti M. A new kind of atlas of zeolite building blocks. J Chem Phys 2019;151:154112.
70. Thompson A, Swiler L, Trott C, Foiles S, Tucker G. Spectral neighbor analysis method for automated generation of quantum-accurate interatomic potentials. J Comput Phys 2015;285:316-30.
71. Zhang L, Han J, Wang H, Car R, E W. Deep potential molecular dynamics: a scalable model with the accuracy of quantum mechanics. Phys Rev Lett 2018;120:143001.
72. Tang L, Yang Z, Wen T, Ho K, Kramer M, Wang C. Short- and medium-range orders in Al90Tb10 glass and their relation to the structures of competing crystalline phases. Acta Materialia 2021;204:116513.
73. Wu J, Zhang Y, Zhang L, Liu S. Deep learning of accurate force field of ferroelectric HfO2. Phys Rev B 2021;103:024108.
74. Yang M, Karmakar T, Parrinello M. Liquid-liquid critical point in phosphorus. Phys Rev Lett 2021;127:080603.
75. Zhang L, Wang H, Car R, Weinan E. Phase diagram of a deep potential water model. Phys Rev Lett 2021;126:236001.
76. Zhang L, Han J, Wang H, et al. End-to-end symmetry preserving inter-atomic potential energy model for finite and extended systems. arXiv preprint arXiv 2018;1805:09003.
77. Naden Robinson V, Zong H, Ackland GJ, Woolman G, Hermann A. On the chain-melted phase of matter. Proc Natl Acad Sci U S A 2019;116:10297-302.
78. Zong H, Robinson VN, Hermann A, et al. Free electron to electride transition in dense liquid potassium. Nat Phys 2021;17:955-60.
79. Zong H, Wiebe H, Ackland GJ. Understanding high pressure molecular hydrogen with a hierarchical machine-learned potential. Nat Commun 2020;11:5014.
80. Novikov IS, Gubaev K, Podryabinkin EV, Shapeev AV. The MLIP package: moment tensor potentials with MPI and active learning. Mach Learn Sci Technol 2021;2:025002.
81. Skinner AJ, Broughton JQ. Neural networks in computational materials science: training algorithms. Modelling Simul Mater Sci Eng 1995;3:371-90.
82. Bholoa A, Kenny S, Smith R. A new approach to potential fitting using neural networks. Nucl Instrum Methods Phys Res B 2007;255:1-7.
83. Behler J, Martonák R, Donadio D, Parrinello M. Metadynamics simulations of the high-pressure phases of silicon employing a high-dimensional neural network potential. Phys Rev Lett 2008;100:185501.
84. Malshe M, Narulkar R, Raff LM, Hagan M, Bukkapatnam S, Komanduri R. Parametrization of analytic interatomic potential functions using neural networks. J Chem Phys 2008;129:044111.
85. Sanville E, Bholoa A, Smith R, Kenny SD. Silicon potentials investigated using density functional theory fitted neural networks. J Phys Condens Matter 2008;20:285219.
86. Eshet H, Khaliullin RZ, Kühne TD, Behler J, Parrinello M. Ab initio quality neural-network potential for sodium. Phys Rev B 2010;81:184107.
87. Handley CM, Popelier PL. Potential energy surfaces fitted by artificial neural networks. J Phys Chem A 2010;114:3371-83.
88. Behler J. Neural network potential-energy surfaces in chemistry: a tool for large-scale simulations. Phys Chem Chem Phys 2011;13:17930-55.
89. Behler J. Atom-centered symmetry functions for constructing high-dimensional neural network potentials. J Chem Phys 2011;134:074106.
90. Artrith N, Morawietz T, Behler J. Erratum: high-dimensional neural-network potentials for multicomponent systems: applications to zinc oxide. Phys Rev B 2012;86:153101.
91. Raff L, Komanduri R, Hagan M, et al. Neural networks in chemical reaction dynamics. OUP USA; 2012.
92. Sosso GC, Miceli G, Caravati S, Behler J, Bernasconi M. Neural network interatomic potential for the phase change material GeTe. Phys Rev B 2012:85.
93. Behler J. Representing potential energy surfaces by high-dimensional neural network potentials. J Phys Condens Matter 2014;26:183001.
94. Behler J. Constructing high-dimensional neural network potentials: a tutorial review. Int J Quantum Chem 2015;115:1032-50.
95. Artrith N, Urban A. An implementation of artificial neural-network potentials for atomistic materials simulations: performance for TiO2. Comput Mater Sci 2016;114:135-50.
96. Hajinazar S, Shao J, Kolmogorov AN. Stratified construction of neural network based interatomic models for multicomponent materials. Phys Rev B 2017;95:014114.
97. Kobayashi R, Giofré D, Junge T, Ceriotti M, Curtin WA. Neural network potential for Al-Mg-Si alloys. Phys Rev Materials 2017;1:053604.
98. Bochkarev AS, van Roekeghem A, Mossa S, Mingo N. Anharmonic thermodynamics of vacancies using a neural network potential. Phys Rev Materials 2019:3.
99. Patra TK, Loeffler TD, Chan H, Cherukara MJ, Narayanan B, Sankaranarayanan SKRS. A coarse-grained deep neural network model for liquid water. Appl Phys Lett 2019;115:193101.
100. Unke OT, Meuwly M. PhysNet: A neural network for predicting energies, forces, dipole moments, and partial charges. J Chem Theory Comput 2019;15:3678-93.
101. Pun GPP, Yamakov V, Hickman J, Glaessgen EH, Mishin Y. Development of a general-purpose machine-learning interatomic potential for aluminum by the physically informed neural network method. Phys Rev Materials 2020;4:113807.
102. Stricker M, Yin B, Mak E, Curtin WA. Machine learning for metallurgy II. A neural-network potential for magnesium. Phys Rev Materials 2020:4.
103. Hajinazar S, Thorn A, Sandoval ED, Kharabadze S, Kolmogorov AN. MAISE: construction of neural network interatomic models and evolutionary structure optimization. Comput Phys Commun 2021;259:107679.
104. Ko TW, Finkler JA, Goedecker S, Behler J. A fourth-generation high-dimensional neural network potential with accurate electrostatics including non-local charge transfer. Nat Commun 2021;12:398.
105. Lin YS, Pun GPP, Mishin Y. Development of a physically-informed neural network interatomic potential for tantalum. arXiv preprint arXiv 2021;2101:06540.
106. Schütt KT, Sauceda HE, Kindermans PJ, Tkatchenko A, Müller KR. SchNet - a deep learning architecture for molecules and materials. J Chem Phys 2018;148:241722.
107. Andolina CM, Williamson P, Saidi WA. Optimization and validation of a deep learning CuZr atomistic potential: Robust applications for crystalline and amorphous phases with near-DFT accuracy. J Chem Phys 2020;152:154701.
108. Hofmann T, Schölkopf B, Smola AJ. Kernel methods in machine learning. Ann Statist 2008;36:1171-220.
109. Müller KR, Mika S, Rätsch G, Tsuda K, Schölkopf B. An introduction to kernel-based learning algorithms. IEEE Trans Neural Netw 2001;12:181-201.
110. Glielmo A, Sollich P, De Vita A. Accurate interatomic force fields via machine learning with covariant kernels. Phys Rev B 2017:95.
111. Bartók AP, Payne MC, Kondor R, Csányi G. Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons. Phys Rev Lett 2010;104:136403.
112. Babaei H, Guo R, Hashemi A, Lee S. Machine-learning-based interatomic potential for phonon transport in perfect crystalline Si and crystalline Si with vacancies. Phys Rev Materials 2019;3:074603.
113. Wang Q, Ding J, Zhang L, Podryabinkin E, Shapeev A, Ma E. Predicting the propensity for thermally activated β events in metallic glasses via interpretable machine learning. npj Comput Mater 2020;6:1-12.
114. Seko A, Maekawa T, Tsuda K, Tanaka I. Machine learning with systematic density-functional theory calculations: application to melting temperatures of single- and binary-component solids. Phys Rev B 2014;89:054303.
115. Zhao L, Zong H, Ding X, Sun J, Ackland GJ. Commensurate-incommensurate phase transition of dense potassium simulated by machine-learned interatomic potential. Phys Rev B 2019;100:220101.
116. Szlachta WJ, Bartók AP, Csányi G. Accuracy and transferability of Gaussian approximation potential models for tungsten. Phys Rev B 2014;90:104108.
117. Artrith N, Behler J. High-dimensional neural network potentials for metal surfaces: A prototype study for copper. Phys Rev B 2012;85:045439.
118. Kruglov I, Sergeev O, Yanilkin A, Oganov AR. Energy-free machine learning force field for aluminum. Sci Rep 2017;7:8512.
119. Dragoni D, Daff TD, Csányi G, Marzari N. Achieving DFT accuracy with a machine-learning interatomic potential: thermomechanics and defects in bcc ferromagnetic iron. Phys Rev Materials 2018;2:013808.
120. Maillet JB, Denoual C, Csányi G. Machine-learning based potential for iron: plasticity and phase transition. AIP Conference Proceedings.. , ;.
121. Ibarra-Hernández W, Hajinazar S, Avendaño-Franco G, Bautista-Hernández A, Kolmogorov AN, Romero AH. Structural search for stable Mg-Ca alloys accelerated with a neural network interatomic model. Phys Chem Chem Phys 2018;20:27545-57.
122. Hajinazar S, Sandoval ED, Cullo AJ, Kolmogorov AN. Multitribe evolutionary search for stable Cu-Pd-Ag nanoparticles using neural network models. Phys Chem Chem Phys 2019;21:8729-42.
123. Sivaraman G, Krishnamoorthy AN, Baur M, et al. Machine-learned interatomic potentials by active learning: amorphous and liquid hafnium dioxide. npj Comput Mater 2020;6:1-8.
124. Artrith N, Hiller B, Behler J. Neural network potentials for metals and oxides - First applications to copper clusters at zinc oxide. Phys Status Solidi B 2013;250:1191-203.
125. Sivaraman G, Gallington L, Krishnamoorthy AN, et al. Experimentally driven automated machine-learned interatomic potential for a refractory oxide. Phys Rev Lett 2021;126:156002.
126. Jain ACP, Marchand D, Glensk A, Ceriotti M, Curtin WA. Machine learning for metallurgy III: a neural network potential for Al-Mg-Si. Phys Rev Materials 2021:5.
127. Zhao L, Zong H, Ding X, Lookman T. Anomalous dislocation core structure in shock compressed bcc high-entropy alloys. Acta Materialia 2021;209:116801.
128. Li QJ, Küçükbenli E, Lam S, et al. Development of robust neural-network interatomic potential for molten salt. Cell Rep Phys Sci 2021;2:100359.
129. Lam ST, Li QJ, Ballinger R, Forsberg C, Li J. Modeling LiF and FLiBe molten salts with robust neural network interatomic potential. ACS Appl Mater Interfaces 2021;13:24582-92.
130. van Duin ACT, Dasgupta S, Lorant F, Goddard WA. ReaxFF: a reactive force field for hydrocarbons. J Phys Chem A 2001;105:9396-409.
131. Cheng B, Mazzola G, Pickard CJ, Ceriotti M. Evidence for supercritical behaviour of high-pressure liquid hydrogen. Nature 2020;585:217-20.
132. Musil F, De S, Yang J, Campbell JE, Day GM, Ceriotti M. Machine learning for the structure-energy-property landscapes of molecular crystals. Chem Sci 2018;9:1289-300.
133. Muhli H, Chen X, Bartók AP, et al. Machine learning force fields based on local parametrization of dispersion interactions: Application to the phase diagram of C60. arXiv preprint arXiv 2021;2105:02525.
134. Caro MA, Csányi G, Laurila T, Deringer VL. Machine learning driven simulated deposition of carbon films: from low-density to diamondlike amorphous carbon. Phys Rev B 2020;102:174201.
135. Rowe P, Deringer VL, Gasparotto P, Csányi G, Michaelides A. An accurate and transferable machine learning potential for carbon. J Chem Phys 2020;153:034702.
136. Caro MA, Deringer VL, Koskinen J, Laurila T, Csányi G. Growth mechanism and origin of high sp3 content in tetrahedral amorphous carbon. Phys Rev Lett 2018;120:166101.
137. Bartók AP, Kermode J, Bernstein N, Csányi G. Machine learning a general-purpose interatomic potential for silicon. Phys Rev X 2018:8.
138. Bonati L, Parrinello M. Silicon Liquid structure and crystal nucleation from ab initio deep metadynamics. Phys Rev Lett 2018;121:265701.
139. Deringer VL, Bernstein N, Csányi G, et al. Origins of structural and electronic transitions in disordered silicon. Nature 2021;589:59-64.
140. Niu H, Piaggi PM, Invernizzi M, Parrinello M. Molecular dynamics simulations of liquid silica crystallization. Proc Natl Acad Sci U S A 2018;115:5348-52.
141. Unruh D, Meidanshahi RV, Goodnick SM, et al. Training a machine-learning driven gaussian approximation potential for Si-H interactions. arXiv preprint arXiv 2021;2106:02946.
142. Deringer VL, Caro MA, Csányi G. A general-purpose machine-learning force field for bulk and nanostructured phosphorus. Nat Commun 2020;11:5461.
143. Niu H, Bonati L, Piaggi PM, Parrinello M. Ab initio phase diagram and nucleation of gallium. Nat Commun 2020;11:2654.
144. Mocanu FC, Konstantinou K, Lee TH, et al. Modeling the phase-change memory material, Ge2Sb2Te5, with a machine-learned interatomic potential. J Phys Chem B 2018;122:8998-9006.
145. Yang Y, Zong H, Sun J, Ding X. Rippling ferroic phase transition and domain switching in 2D materials. Adv Mater 2021:e2103469.
146. Hajibabaei A, Kim KS. Universal machine learning interatomic potentials: surveying solid electrolytes. J Phys Chem Lett 2021;12:8115-20.
147. Hajibabaei A, Myung CW, Kim KS. Sparse Gaussian process potentials: application to lithium diffusivity in superionic conducting solid electrolytes. Phys Rev B 2021;103:214102.
148. Kostiuchenko T, Körmann F, Neugebauer J, Shapeev A. Impact of lattice relaxations on phase transitions in a high-entropy alloy studied by machine-learning potentials. npj Comput Mater 2019;5:1-7.
149. Lahnsteiner J, Jinnouchi R, Bokdam M. Long-range order imposed by short-range interactions in methylammonium lead iodide: comparing point-dipole models to machine-learning force fields. Phys Rev B 2019;100:094106.
150. Lapointe C, Swinburne TD, Thiry L, et al. Machine learning surrogate models for prediction of point defect vibrational entropy. Phys Rev Materials 2020;4:063802.
Cite This Article
Export citation file: BibTeX | RIS
OAE Style
Yang Y, Zhao L, Han CX, Ding XD, Lookman T, Sun J, Zong HX. Taking materials dynamics to new extremes using machine learning interatomic potentials. J Mater Inf 2021;1:10. http://dx.doi.org/10.20517/jmi.2021.001
AMA Style
Yang Y, Zhao L, Han CX, Ding XD, Lookman T, Sun J, Zong HX. Taking materials dynamics to new extremes using machine learning interatomic potentials. Journal of Materials Informatics. 2021; 1(2): 10. http://dx.doi.org/10.20517/jmi.2021.001
Chicago/Turabian Style
Yang, Yang, Long Zhao, Chen-Xu Han, Xiang-Dong Ding, Turab Lookman, Jun Sun, Hong-Xiang Zong. 2021. "Taking materials dynamics to new extremes using machine learning interatomic potentials" Journal of Materials Informatics. 1, no.2: 10. http://dx.doi.org/10.20517/jmi.2021.001
ACS Style
Yang, Y.; Zhao L.; Han C.X.; Ding X.D.; Lookman T.; Sun J.; Zong H.X. Taking materials dynamics to new extremes using machine learning interatomic potentials. J. Mater. Inf. 2021, 1, 10. http://dx.doi.org/10.20517/jmi.2021.001
About This Article
Copyright
Data & Comments
Data
Cite This Article 23 clicks
Like This Article 1
likes
Comments
Comments must be written in English. Spam, offensive content, impersonation, and private information will not be permitted. If any comment is reported and identified as inappropriate content by OAE staff, the comment will be removed without notice. If you have any queries or need any help, please contact us at support@oaepublish.com.